トップページ

第３章 外力と内力

3.1 外力

　構造物に作用する外力は、物体の内部に直接作用する力、
　いわゆる物体力と構造物の表面に作用する表面力に分けられます。
　前者は、構造物自体の重さに関係する重力、遠心力などです。
　後者は、構造物の表面に作用する荷重及び支点反力です。
　しかし、自重などの物体力は、その構造物を構成する各質点に作用しますが、
　その力学的効果は、表面力としての荷重と等しい効果を表します。
　そのため、自重も荷重として取り扱うのが一般的です。

　表面力や物体力が構造物に作用するとき、
　構造物が静止、安定の状態にあるのは、
　地盤または他の構造物に結合されているためで、
　この結合点を支点といいます。
　支点に生じている力を支点反力といい、物体力と表面力の和に等しい。
　つまり、構造物に作用する外力は、自重を含めた荷重と支点反力との２種類となります。

　具体的に荷重には、水圧、風力、地震力、自動車・電車のような交通荷重
　あるいは、構造物自体の重さ（死荷重）があります。
　構造物に荷重を作用させるには、静力学では力が徐々に作用し、
　その間に衝撃や振動が発生しないと仮定しています。
　そのため変位も最初の０から直線的に増大してその最終値にいたります。
　荷重は、力の作用状態によって次のように分類することができます。

（力の分布状態による荷重の分類）

（力の向きによる荷重の分類）

荷重を力の向きによって分けると、次のように分類することができます。

引張荷重：物体を引き伸ばすように働く荷重

圧縮荷重：物体を押し縮めるように働く荷重

せん断荷重：物体をハサミで切るように働く荷重

曲げ荷重：物体を曲げるように働く荷重

3.2 内力

　内力とは、外力の作用に応じて物体内に生ずる作用・反作用の一対の力です。
　つまり、物体が一定の形を保持するため物体内の仮想の断面相互間に働く力であり、
　断面力と呼ばれます。
　応力は、単位面積当たりの内力のことです。

１）棒の両端に外力Ｐを作用させます。その結果、
　棒が断面a−aで切断され左右に分離（仮想切断）したと考えると、
　・このままでは、棒は左右に離れ、元の状態を保てません。
２）切り離した状態でも棒が左右に分離しないで元の位置に留まっているための力学的条件を考えます。
　　○棒が離れていくのは、
　　　・左の部分では外力Pが左向きに作用、
　　　・右の部分では外力Pが右向きに作用、
　　○実際には棒は動かないから、
　　　・仮想的に切断した断面a−aには、外力Ｐに対抗する力Ｎ1、Ｎ2が作用しているはずです。
　　○すなわち、
　　　・仮想切断面a−aを介して互いに力を及ぼし合い棒は切れないでいます。この力を内力と呼びます。
　　○この内力Ｎ1，Ｎ2は、
　　　・仮想的に切断されたそれぞれの部分で、力のつり合いを満たしていなければならない。
　　　・また、作用・反作用の関係にあります。
　　図では，力のつり合い条件式よりＮ1 ,Ｎ2は次のように求まります。
　　Ｐ＋Ｎ1＝0　→　Ｎ1＝−Ｐ （Ｎ1は右向き）
　　Ｎ2＋Ｐ＝0　→　Ｎ2＝−Ｐ （Ｎ2は左向き）
　　∴　　Ｎ1＝Ｎ2 すなわち、
　　Ｎ1 とＮ2 は大きさが同じであり作用方向は逆向きです。
　　以上のことから次の結論が得られます。

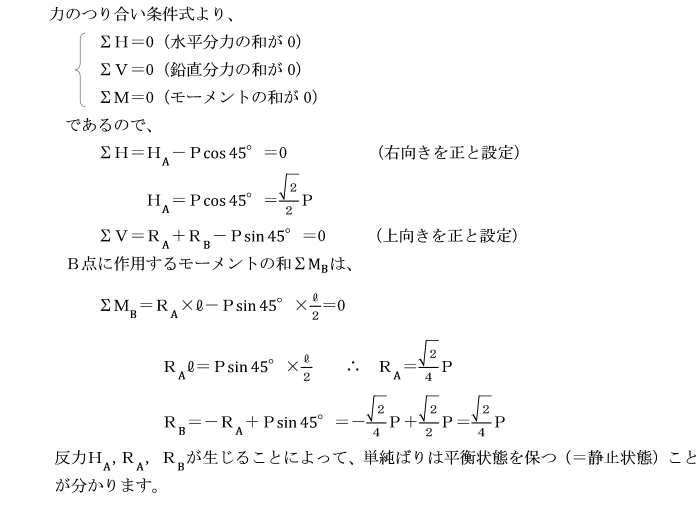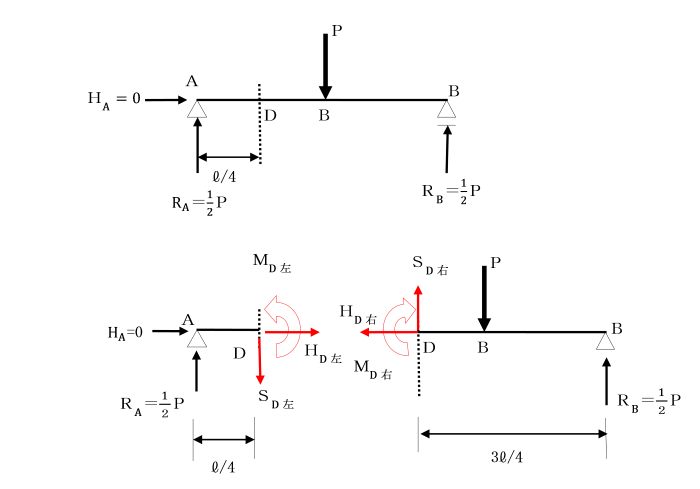
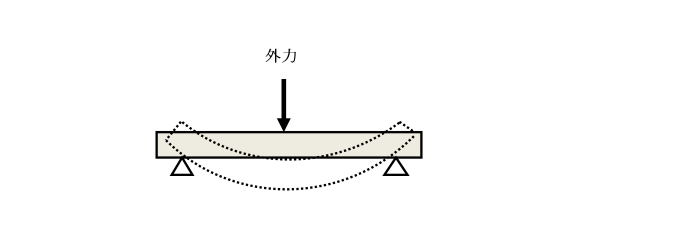
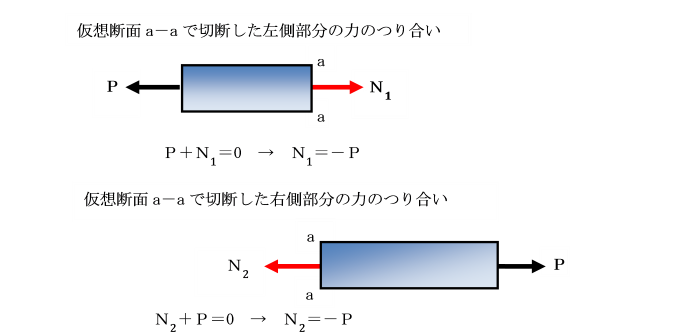
仮想切断面a-aには、それぞれ分離した部分に、
　外力とつり合う力が働いています。
　この仮想切断面に生じる力を内力と呼ぶ。
　そして、内力については次のことが言えます。

○　仮想切断によって物体は２分され、仮想切断面も２つ現れます。
　各々の断面上に生じる内力は、それが含まれる部分の外力とつり合う。

そして、それらは大きさが等しく方向が逆である。（作用・反作用）

○　内力は、いずれか一方の部分について、
　力のつり合いを考えることにより、求めることができます。

3.3 外力と内力の関係

　物体に外力が作用すると、一般的に変形が生じます。
　その変形に抵抗し、物体の連続的な形状を保持しようとするため内力が生じます。
　言い換えれば、外力は物体を変形させる原因であり、
　物体はこれに対抗して元の形を保とうとする結果、
　内部に力が発生して、その外力に耐えようとします。その力を内力といいます。

　棒の任意断面の左または右に作用している外力（支点反力含む）が、
　その断面に与える影響を考えるということは、
　その外力によって、その断面に内力の形で生じる力、
　すなわち、軸方向力、せん断力及び曲げモーメント(横断面の図心に関する偶力モーメント)の
　影響を調べることに置き換えられます。
　３つの力は断面に生ずる力であるので、
　総称して断面力といいます。
　荒っぽくいうと断面力は、断面全体に生じている内力です。

　それでは、外力が断面力としてどのように置き換えられるかを調べてみましょう。
　今、はりの左側の端Ａから任意の距離Ｘのところに垂直な断面a−aを考えます。
　ここで棒を仮想的に切断して左側のみを考えます。
　切断した部分で、その系はつり合い状態にならなければなりません。
　外力Ｐ1、Ｐ2、Ｐ3の合力Ｒを考えます。
　合力Ｒは一般的に鉛直でないから、その作用線を延長すると、
　断面a−aの延長線と交わります。
　この点をＣとして、その点で合力Ｒの方向、大きさを表します。

　次に、断面a−aの左側の部分において、
　合力Ｒを断面a−aに対して垂直と接線方向の分力ＮとＳに分けます。
　断面に対して接線方向であるＳは、棒ＡＢをa−aでせん断しようとする力です。

　続いてＮについて調べるために、
　棒の軸ＡＢと断面a−aとの交点ＧにＮと大きさ、方向は等しいが、
　向きが反対であるような２つの力ＮB、Ｎ@を仮定してみます。
　このＮB、Ｎ@の２力は互いに打ち消し合うからＧ点に、
　この２つのＮB、Ｎ@を加えても、つり合いの関係は変わらません。
　ＮB、Ｎ@を利用すると、Ｇ点に加えた左向きのＮ@とＣ点に働く右向きのＮAとを考えると、
　この２力は偶力モーメントＭ＝Ｎ・ｙを生じます。

　Ｇ点に仮定したもう１つの右向きのＮBという力は、そのまま残ります。
　結局、棒の軸Ｇを通るＮBと偶力モーメントＭとの２つに置き換えられます。
　図心軸に作用する軸方向の力を軸方向力という。

　この偶力モーメントＭは、断面a−aにおいて棒ＡＢを曲げようとするもので、
　特に曲げモーメントと呼ぶ。
　このように外力は断面力（軸方向力Ｎ、せん断力Ｓ及び曲げモーメントＭ）に置き換えられることが分かります。

　内力は、外力の作用に応じて物体内に置き換えられたものであるので、
　外力と内力は平衡状態、つまり物体は、静止状態にあります。
　単純ばりを例にとり、さらに調べてみましょう。
　はりとは、丸木橋のように荷重に抵抗する棒をいい、
　主として曲げによって荷重に抵抗する構造物です。
　はりの種類と支点の種類については、「第４章　はり理論　4.5 静定構造物の解法」で解説しますが、
　ここでは、外力と内力の関係を調べてみます。

3.3.1　外力系のつり合い

　図のように、はり部材のＡ点が回転のみ可能な回転支点（ピン支点）、
　Ｂ点を水平移動と回転可能な可動支点（ローラー支点）で
　支えられた状態を「単純ばり」という。
　単純ばりに外力Ｐが作用すると、支点はそれに抵抗する反力を生じます。

　図のように長さlの単純ばりに外力Ｐが作用する場合について考えてみましょう。
　回転支点をＡ、可動支点をＢとします。
　この単純ばりは図のように支点反力ＨA,ＲA,ＲBが生じます。

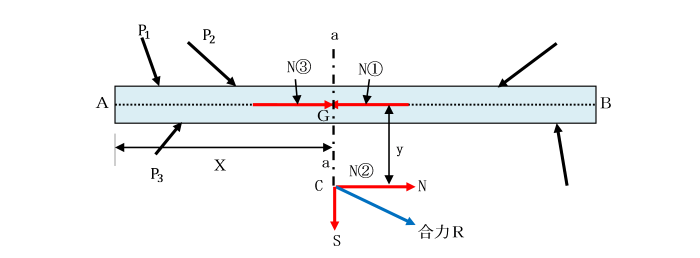
外力と反力の関係（外力系のつり合い）

@　はりに外力が作用した際、はりは静止しているため、
　支点はそれに抵抗する反力を生じます。

A　支点は、外力とつり合う力が生じます。
　つまり、外力と反力の合力は0となります。

B　外力と反力の合力が0ということは、はりに作用する力（＝外力及び反力）が、
　つり合っていることを意味します。

C はりに作用している力がつり合うということは、
　はりが静止状態（平衡状態）を保つことを意味します。

3.3.2　内力系のつり合い

　外力と反力のつり合いを外力系のつり合いと呼ぶのに対し、
　部材内部の力のつり合いを内力系のつり合いという。
　例えば、下図のような単純ばりを考えます。

　外力Ｐに対し、支点Ａ,Ｂは、
　はりを静止状態に保つために反力が生じます。
　はりが静止状態を保つためには、はりが移動、かつ回転しないことなので、
　力のつり合い条件式を満たす必要があります。

力のつり合い条件式より、
　ΣＨ＝０（水平分力の和が０）
　ΣＶ＝０（鉛直分力の和が０）
　ΣＭ＝０（モーメントの和が０）　より、
　ΣＨ＝ＨA＝０
　ΣＶ＝ＲA＋ＲB−Ｐ＝０
　Ｂ点に作用するモーメントの和ΣＭBは、
　ΣＭB＝ＲA×l−Ｐ×l/２＝０
　ＲA＝1/２Ｐ　、ＲB＝−ＲA＋Ｐ＝(1/２)Ｐ
　したがって、外力系のつり合いより静止状態を保ちます。
　次に、内力系のつり合いを考えます。この単純ばりの任意の点Ｄにおける内力の値を求めます。
　図のように点Ｄを仮想的に切断してみます。

　部材左側部分の内力系のつり合いを考えます。
　静止状態を保つために点Ｄは、
　内力ＨD左,ＳD左,ＭD左が生じます。

　外力系の力のつり合いより、はり全体は静止状態を保っているため、
　部材内部の点Ｄも静止状態を保つことになります。
　点Ｄが静止状態を保つためには、
　点Ｄの左側部分におけるつり合い条件式が成立する必要があります。
　Ｄの左側部分におけるつり合い条件式

　ΣＨ＝ＨD左＝０
　ΣＶ＝Ｐ/２−ＳD左＝０
　Ｄ点に作用するモーメントの和ΣＭDは、
　ΣＭD＝(Ｐ/２)×l/４−ＭD左＝０　（時計回りを正と設定)
　したがって、ＨD左＝０
　ＳD左＝Ｐ/２（下向き）　、ＭD左＝Ｐｌ/８（反時計回り）となります。
　つまり、任意の点Ｄにおいて内力が生じることで静止状態を保つ。
　このことを内力系のつり合いという。
　次に、部材右側部分の内力系のつり合いを求めてみましょう。
　部材の左側同様、点Ｄが静止状態にあるためには、つり合い条件式が成立します。
　ΣＨ＝ＨD右＝０
　ΣＶ＝−Ｐ/２＋Ｐ−ＳD右＝０
　Ｄ点に作用するモーメントの和は、
　ΣＭD＝Ｐ/２×３l/４−Ｐ×l/４−ＭD右＝０　(反時計回りを正と設定)
　したがって、ＨD左＝０
　ＳD左＝Ｐ/２（上向き）
　ＭD右＝Ｐl/８（時計回り）　　となります。
　部材の左側から求めた点Ｄの内力ＨD左,ＳD左,ＭD左と
　右側から求めた点Ｄの内力ＨD右,ＳD右,ＭD右を比べてみると、
　大きさが等しく向きが逆であることが分かります。

　任意の断面に生じる内力は作用・反作用の関係から必ず大きさが等しく逆方向の力となります。
　任意の点における内力は、どちらの側からも求めることができます。

トップページ