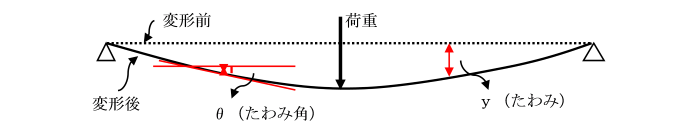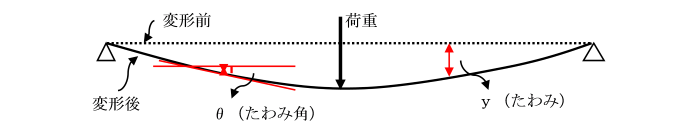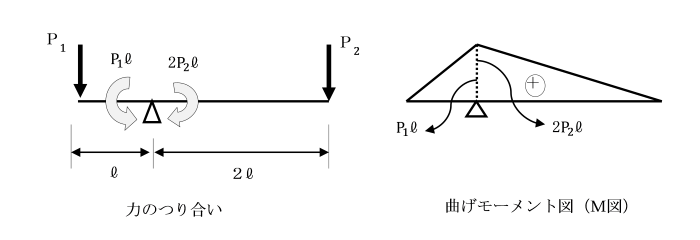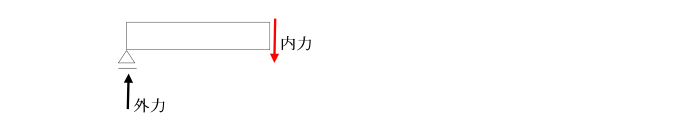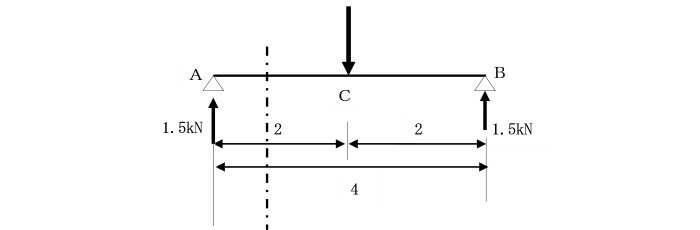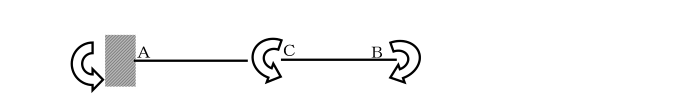僩僢僾儁乕僕
戞係復 偼傝棟榑
4.1 奣愢
丂儀儖僰乕僀丒僆僀儔乕偺暯柺曐帩偺壖掕偵婎偯偄偨屆揟嬋偘棟榑乮弶摍嬋偘棟榑乯偼丄
丂偼傝偼曄宍偺慜屻偱丄抐柺宍忬偑曄壔偟側偄偲偄偆峫偊偱偡丅
丂偮傑傝曄宍慜偵丄偼傝偺拞棫幉偵捈岎偟偰偄偨擟堄抐柺偼丄
丂曄宍屻傕拞棫幉偵捈岎偡傞偲偄偆傕偺偱丄
丂偼傝偺偣傫抐曄宍偼峫椂偟傑偣傫丅
丂幚嵺丄墶壸廳傪庴偗偨偼傝偼丄
丂偣傫抐墳椡偑惗偠偰偄傞偺偱丄偣傫抐曄宍偑敽偄傑偡丅
丂捠忢偺偼傝偱偼丄嬋偘曄宍偑偣傫抐曄宍偵斾傋戩墇偟偰偄傞偺偱丄
丂嬋偘曄宍偺傒傪峫偊傞偙偲偱廫暘偱偡丅
丂偟偐偟丄偼傝偺崅偝h偲僗僷儞l偺斾h/l偑憹戝偡傞偵偮傟丄
丂抐柺偑備偑傒丄偣傫抐曄宍偺塭嬁偑柍帇偡傞偙偲偑偱偒側偔側傝傑偡丅
丂偮傑傝丄抐柺悺朄偵斾傋偰挿偝偑抁偄偼傝傗丄屌掕抂偺傛偆偵抐柺峉懇偺嫮偄晹暘偱偼丄
丂偣傫抐曄宍偺塭嬁偑戝偒偔側傝傑偡丅
4.2 抏惈峔憿椡妛偺壖掕
丂抏惈峔憿椡妛偵偍偄偰庢傝埖偆斖埻偼丄
丂摿偵抐傜側偄尷傝師偺帠崁傪壖掕偟偰偄傑偡丅
- 奜椡偼惷揑偵嶌梡偟傑偡丅
- 峔憿嵽椏偼丄嬒幙丄摍曽惈偱偁傝丄僼僢僋偺朄懃偵偟偨偑偆丅
- 峔憿暔偺曄宍偼丄偦偺悺朄偵斾傋偰旝彫偱偁傝丄旝彫曄宍棟榑偵偟偨偑偆丅
亙惷揑嶌梡亜
丂抏惈懱偵壸廳傪嶌梡偝偣傞嵺偵丄怳摦丄徴寕傪梌偊側偄傛偆偵偡傞偨傔丄
丂壸廳傪侽偐傜彊乆偵壛偊巒傔丄嵟廔抣傑偱憹戝偝偣傞嵹壸曽朄傪惷揑嶌梡偲偄偄傑偡丅
丂摉慠丄曄埵傕嵟弶偺侽偐傜捈慄揑偵憹壛偟偰嵟廔抣偵偄偨傝傑偡丅
亙嬒幙丄摍曽惈亜
丂嵽椏偺偳偺応強偱傕墳椡亅傂偢傒娭學偑摨堦偱偁傞惈幙傪嬒幙偲偄偄丄
丂偙偺傛偆側惈幙傪帩偭偨嵽椏偼嬒幙懱偲屇傇丅
丂応強枅偵墳椡亅傂偢傒娭學偑堎側傞嵽椏偼旕嬒幙懱偲偄偆丅
丂傑偨丄壸廳偵懳偡傞曄宍偑曽岦偵埶懚偟側偄丅
丂偮傑傝丄墳椡亅傂偢傒娭學偑偳偺曽岦偱偁偭偰傕摍偟偄惈幙傪摍曽惈偲偄偄丄
丂偙偺傛偆側惈幙傪帩偭偨嵽椏傪摍曽惈懱偲屇傇丅
丂曄宍偑曽岦偵傛偭偰堎側傞惈幙傪堎曽惈偲偄偄丄
丂偙偺傛偆側惈幙傪帩偭偨嵽椏偼堎曽惈懱偲偄偄傑偡丅
亙僼僢僋偺朄懃亜
丂儘僶乕僩乚僼僢僋(Robert Hooke,僀僊儕僗,1635乣1703)偼丄
丂懡偔偺嵽椏幚尡偐傜嵽椏偵壛傢傞椡偺戝偒偝偲丄
丂偦傟偵傛傞嵽椏偺曄宍偺戝偒偝偲偺娭學傪柧妋偵偟偨丅
丂暔懱偑抏惈偺斖埻傪挻偊側偄応崌丄墳椡偲傂偢傒偺斾偼摍偟偄丅
丂墳椡偲傂偢傒偺娫偵偼嵽椏偵傛偭偰屌桳偺娭學偑偁傝傑偡丅
丂堷挘傗埑弅偺偲偒偺墳椡偲傂偢傒偺斾傪儎儞僌棪丄
丂偣傫抐墳椡偲偣傫抐傂偢傒偺斾傪偣傫抐抏惈學悢偲偄偆丅
亙旝彫曄宍棟榑亜
丂峔憿暔偼奜椡傪庴偗偰曄宍偟傑偡偑丄
丂偦偺曄宍偼峔憿暔慡懱偺悺朄偵斾妑偡傞偲旕忢偵旝彫側傕偺偱偡丅
丂奜椡偺嶌梡偟偨忬懺偱偮傝崌偄傪峫偊傞応崌丄
丂奜椡偺嶌梡偡傞埲慜偺悺朄傪偦偺傑傑巊梡偟偰傕嵎偟巟偊側偄丅
丂偙偺峫偊傪旝彫曄宍棟榑偲偄偆丅
丂曄宍偑旝彫偱偁傞偨傔偵丄墳椡偺偮傝崌偄媦傃墳椡偲奜椡偺偮傝崌偄偑丄
丂曄宍慜偺崪慻傒偺宍忬丄忬懺偱惉棫偡傞偲偄偆壖掕偱偡丅
丂偮傝崌偄幃傪峫偊傞偲偒偵丄峔憿暔撪偵旝彫側棫曽懱偺憡懳偡傞奺柺偼暯峴偱丄
丂偐偮摨偠柺愊偱偁傞偲尒側偡丅
丂偮傑傝宍偑曄傢偭偰偟傑偆偲偄偆偙偲偼峫偊側偄丅
丂偙偺偨傔丄曄宍慜偺崪慻傒偺宍忬丄忬懺偱偮傝崌偄幃傪揔梡偟傑偡丅
4.3 夝愅偺婎杮尨棟
丂峔憿暔偺墳椡偲曄宍傪嶼掕偡傞偨傔偵偼丄
丂嘆椡偺偮傝崌偄忦審
丂嘇抏惈忦審乮墳椡偲曄宍偲偺娭學乯
丂嘊曄宍偺揔崌忦審
丂偺俁屄偺忦審傪幃偵昞偟丄
丂偙傟傜偺忦審偵揔崌偡傞楢棫堦師曽掱幃傪夝偔昁梫偑偁傝傑偡丅
丂嘆偼丄惷椡妛揑偮傝崌偄忦審偱偁傝丄
丂暯柺峔憿偱偼丄悈暯椡偺榓偑侽乮儼俫亖侽乯丄
丂墧捈椡偺榓偑侽乮儼倁亖侽乯
丂媦傃儌乕儊儞僩偺榓偑侽乮儼俵亖侽乯傪巜偡丅
丂惷掕峔憿暔偼偙偺偮傝崌偄忦審偺傒傪梡偄偰夝偔偙偲偑偱偒傑偡丅
丂嘇偼丄抏惈懱偵偍偄偰丄僼僢僋偺朄懃偐傜摫偐傟傞傕偺偱丄
丂墳椡偲傂偢傒偑慄宍娭學偱梌偊傜傟傑偡丅
丂嘊偺曄宍偺揔崌忦審偲偼丄
丂椺偊偽丄抂巟揰丄拞娫巟揰偺偨傢傒偑侽偵側傞偙偲傗丄
丂偨傢傒妏偺楢懕惈側偳傪堄枴偟偰偄傑偡丅
丂偙偙偱丄偨傢傒丄偨傢傒妏偲偼丄
丂曄宍慜偺偼傝偺拞怱幉偐傜丄曄宍屻偺丄偼傝偺拞怱幉偺曄埵傪偨傢傒偲屇傃丄
丂偨傢傒嬋慄偺愙慄偲曄宍慜偺偼傝偺拞怱幉偲偺側偡妏傪偨傢傒妏偲偄偆丅
4.4 峔憿暔偺庬椶
4.4.1 峔憿暔偺暘椶
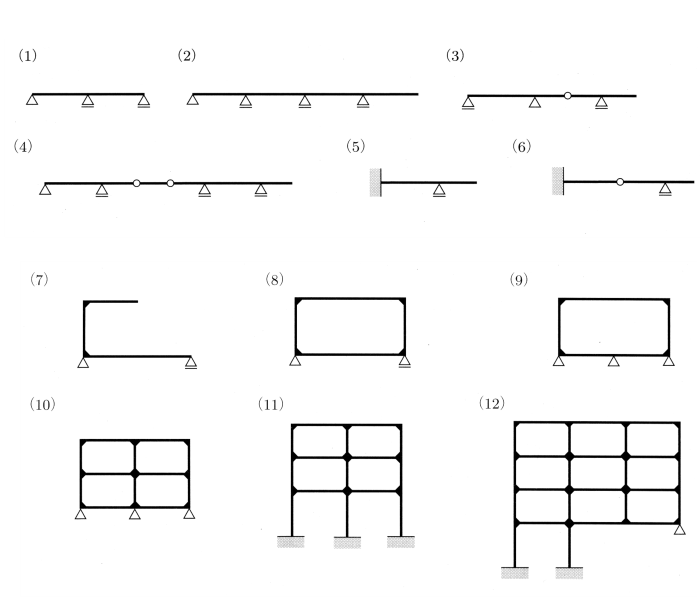
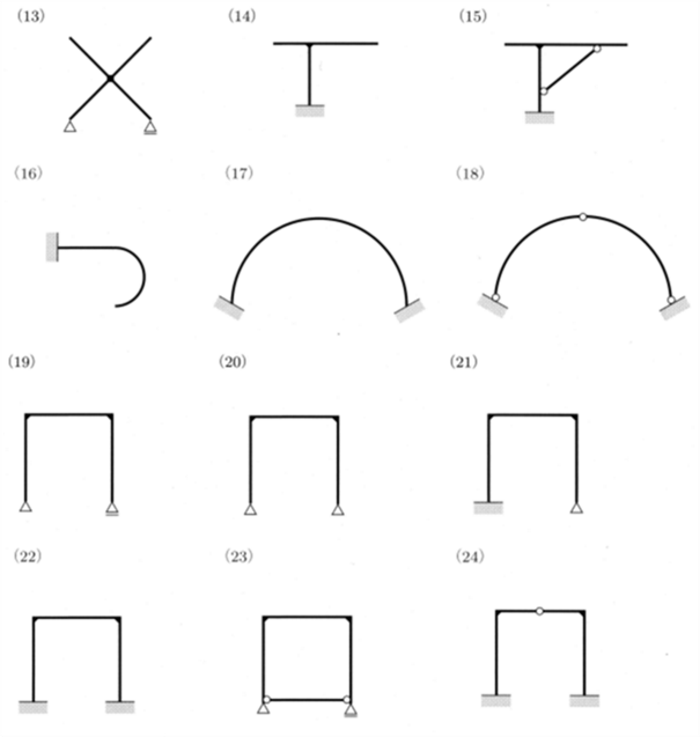
峔憿暔傪暘椶偡傞偲師偺傛偆偵昞偝傟傑偡丅
4.4.2 峔憿暔偺埨掕丄晄埨掕偲惷掕丄晄惷掕
嘆丂奜揑埨掕丄奜揑晄埨掕
丂奜揑偲偼丄峔憿暔慡懱偺埵抲偺忬嫷乮堏摦丄夞揮偺桳柍乯傪堄枴偟丄
丂撪揑偲偼丄峔憿晹嵽偺宍忬偺忬嫷乮峔憿宯偲偟偰偺掞峈偺桳柍乯傪堄枴偡傞傕偺偱偡丅
丂峔憿暔偑奜椡傪庴偗偰曄宍偼偡傞偑丄堏摦傕夞揮傕偟側偄忬懺傪奜揑埨掕偲偄偆丅
丂偮傑傝丄椡偺揱払偑峴傢傟丄斀椡丄晹嵽椡偑妋掕偱偒傑偡丅
丂峔憿暔偑堏摦傗丄夞揮偡傞傛偆側忬懺傪奜揑晄埨掕偲偄偄丄
丂椡偺偮傝崌偄忦審偑惉棫偟側偄丅
丂偙偺傛偆偵奜揑埨掕丄奜揑晄埨掕偼丄巟帩忦審偵傛傞埨掕丄晄埨掕傪堄枴偟傑偡丅
嘇丂奜揑惷掕丄奜揑晄惷掕
丂椡偺偮傝崌偄忦審偺傒偱峔憿暔偺斀椡傪媮傔傞偙偲偑偱偒傞偲偒丄
丂偦偺峔憿暔偼奜揑惷掕偲偄偆丅
丂椡偺偮傝崌偄忦審偺懠偵丄
丂峔憿暔偺曄宍忦審傪峫椂偟側偗傟偽丄
丂斀椡傪媮傔傞偙偲偑偱偒側偄峔憿暔偼丄奜揑晄惷掕偱偡丅
嘊丂撪揑惷掕丄撪揑晄惷掕
丂僩儔僗峔憿側偳丄晹嵽偺抐柺椡偑丄
丂偮傝崌偄忦審偺傒偱寛掕偱偒傞峔憿傪撪揑惷掕偲偄偆丅
丂偮傝崌偄忦審偺傒偱寛掕偱偒側偄峔憿傪撪揑晄惷掕偲偄偆丅
丂撪揑偲偼丄峔憿暔偺宍忬偺埨掕傪堄枴偟傑偡丅
嘋丂撪揑埨掕丄撪揑晄埨掕
丂僩儔僗峔憿側偳偱偼丄峔憿懱傪峔惉偡傞晹嵽悢偑廫暘偱丄
丂奜椡偵懳偟偰掞峈偱偒傞峔憿傪撪揑埨掕偲偄偆丅
丂奜揑偵埨掕偱偁偭偰傕峔憿懱傪峔惉偡傞晹嵽悢偑晄廫暘偱偁傞偲丄
丂峔憿宯偑晄埨掕偲側傞丅
丂偙傟傪撪揑晄埨掕偲偄偆丅
丂撪揑晄埨掕側峔憿偼奜椡偑嶌梡偡傞偲丄峔憿宯偲偟偰掞峈偱偒偢曵夡偟傑偡丅
嘍丂慡惷掕丄慡晄惷掕
丂儔乕儊儞傗傾乕僠偺傛偆側峔憿偱偼丄
丂撪揑惷掕丄晄惷掕偱偼側偔丄
丂撪揑惷掕偲奜揑惷掕傪崌傢偣偨慡惷掕忦審偑廳梫偱偡丅
4.4.3 惷掕峔憿暔
丂惷椡妛偺暯峵曽掱幃乮偮傝崌偄忦審幃儼俫=0丄儼倁亖侽丄儼俵亖侽乯偵傛偭偰
丂巟揰斀椡傗抐柺椡偺戝偒偝傪寛掕偱偒傞峔憿暔偱偡丅
丂俫丗壸廳媦傃斀椡偺悈暯惉暘
丂倁丗壸廳媦傃斀椡偺墧捈惉暘
丂俵丗壸廳媦傃斀椡偺擟堄揰傑傢傝偺儌乕儊儞僩
埨掕傪曐偮偨傔丄埵抲偑晄曄偐偮宍忬偑晄曄偺忦審傪枮偨偡偨傔偵嵟彫尷偺峉懇偐傜惉傝棫偮峔憿暔偱偡丅
4.4.4 晄惷掕峔憿暔
丂椡偺偮傝崌偄忦審幃偺傒偱偼丄
丂巟揰斀椡傗抐柺椡偺戝偒偝傪寛掕偱偒側偄峔憿暔偱偡丅
丂峔憿夝愅偵偼丄偝傜偵晄惷掕師悢偵憡摉偡傞悢偺曄宍偺揔崌忦審幃傕昁梫偲側傝傑偡丅
丂埨掕傪曐偮偨傔丄嵟彫尷昁梫側峉懇傛傝懡偔偺峉懇傪庴偗偰偄傞峔憿暔偱偁傞丅
丂偦偺偨傔丄惷掕峔憿暔偵斾傋偰椡妛揑偵埨慡惈偑崅偄丅
丂値師晄惷掕峔憿暔偼丄惷掕峔憿暔偵懳偟丄偝傜偵値屄偺峉懇傪梌偊偨峔憿暔偱偡丅
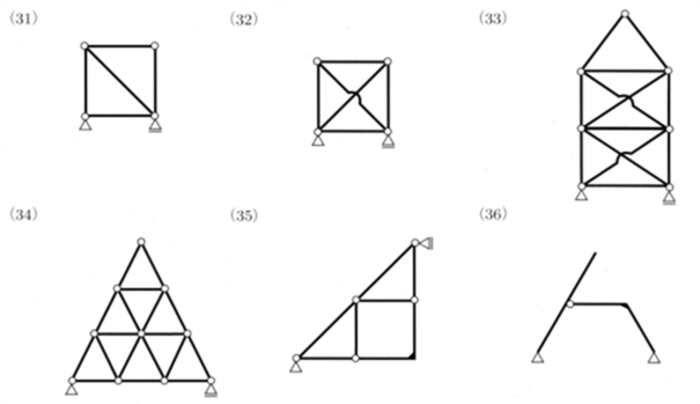
4.4.5丂峔憿暔偺晄惷掕惈
丂晄惷掕師悢偼丄峔憿暔偺埨掕傪曐偮偨傔丄
丂嵟彫尷昁梫側峉懇傛傝偳傟偩偗懡偔偺峉懇偑梌偊傜傟偰偄傞偐傪昞偡悢偱偡丅
丂偟偨偑偭偰丄惷掕峔憿暔偺晄惷掕師悢偼侽偱偁傝丄
丂惷掕峔憿暔偐傜1偮偱傕峉懇傪庢傝嫀傞偲晄埨掕側峔憿暔偵側傝傑偡丅
丂堦斒揑偵峔憿暔偺晄惷掕師悢偼丄
丂奜揑媦傃撪揑晄惷掕師悢偺憤榓偱偡丅
丂晄惷掕峔憿暔偺夝愅偱偼丄
丂晄惷掕師悢偵憡摉偡傞悢偺椡傪枹抦検偲偟偰寛掕偡傟偽丄
丂懠偺椡乮斀椡傗抐柺椡乯偼丄椡偺偮傝崌偄忦審幃偐傜媮傔傞偙偲偑偱偒傑偡丅
丂枹抦検偲偟偰慖掕偟偨椡傪晄惷掕椡偲偄偆丅
丂晄惷掕峔憿暔偐傜夁忚側斀椡偑庢傝彍偐傟偨屻偵巆傞峔憿暔偼丄
丂惷掕婎杮宯偲屇偽傟丄庢傝彍偐傟偨斀椡傪晄惷掕検偲偄偄傑偡丅
亙晄惷掕師悢偺敾暿幃亜
n亖m亄r亄p亅2k
丂n丗晄惷掕師悢
丂丂n亙0丂丂晄埨掕乮峔憿暔偲偟偰婡擻偟側偄乯
丂丂n亖0丂丂惷掕峔憿暔
丂丂n亜0丂丂晄惷掕峔憿暔乮値偺抣偑晄惷掕師悢偲側傞乯
丂丂丂m丗晹嵽悢
丂丂丂r丗斀椡悢乮壜摦巟揰亖侾丂夞揮巟揰亖俀丂屌掕巟揰亖俁乯
丂丂丂p丗崉愡愙崌嵽悢乮崉愡偵愙崌偟偰偄傞晹嵽偺悢乯
崉愡愙崌嵽悢p 偲偼丄偁傞晹嵽偵拝栚偟偨偲偒偵丄偦偺晹嵽偵崉偵愙崌偝傟偰偄傞晹嵽偺悢傪昞偟偰偄傑偡丅偦傟偧傟偺愡揰偵愙崌偟偰偄傞晹嵽偺悢帤偺嵟戝抣偑偦偺愡揰偺崉愡愙崌嵽悢
丂k丗愡揰悢乮巟揰丄帺桼抂傕侾偮偺愡揰偲悢偊傑偡乯
亂椺戣係亅侾亃
丂師偺峔憿暔偼丄惷掕峔憿暔偐晄惷掕峔憿暔偐摎偊傛丅晄惷掕峔憿暔偺応崌偼丄晄惷掕師悢傕摎偊傛丅(惷掕丒晄惷掕)
亂夝摎係亅侾亃
4.5 惷掕峔憿暔偺夝朄
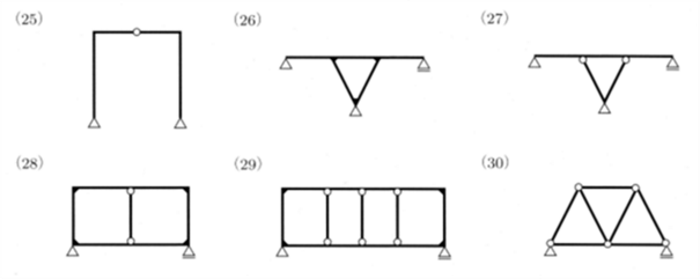
4.5.1丂偼傝偺庬椶
偼傝傪峔憿偵傛偭偰暘偗傞偲師偺傛偆側傕偺偑偁傝傑偡丅
乮侾乯扨弮偽傝
丂丂丂侾偮偺偼傝偑椉抂偱巟偊傜傟丄偦偺堦抂偑夞揮巟揰偱偁傝丄
丂丂丂懠抂偑壜摦巟揰偱巟偊傜傟偰偄傞傕偺丅
乮俀乯曅帩偽傝
丂丂丂堦抂偑屌掕巟揰偱丄懠抂偼帺桼側忬懺偵側偭偰偄傞傕偺丅
乮俁乯挘弌偽傝
丂丂丂巟揰偺峔憿偼丄扨弮偽傝偲摨偠偱偁傞偑丄
丂丂丂偼傝偺堦抂傑偨偼椉抂偑巟揰偐傜奜懁偵挘傝弌偟偰偄傞傕偺丅
乮係乯屌掕偽傝
丂丂丂偼傝偺椉抂偑杽傔崬傑傟偰屌掕偟偨傕偺丅
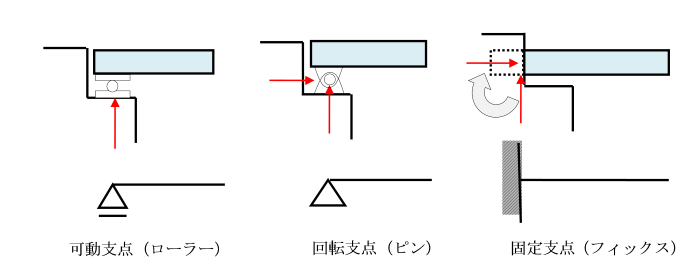
4.5.2丂巟揰偺庬椶偲斀椡悢
丂搚栘峔憿暔偼捠忢抧斦忋偵峔抸偝傟傑偡丅
丂偦偺抧斦偲峔憿暔偺愙揰傪巟揰偲偄偆丅
丂巟揰偵偼寢崌偺巇曽偵傛傝丄壜摦巟揰乮儘乕儔乕巟揰乯丄
丂夞揮巟揰乮僺儞巟揰乯丄
丂屌掕巟揰乮僼傿僢僋僗巟揰乯偺俁庬椶偑偁傝傑偡丅
丂巟揰偵偍偗傞峉懇偺搙崌偄傪峉懇搙偲偄偆丅
丂壜摦巟揰偼悈暯曽岦偵堏摦偑壜擻偱偁傝丄
丂偼傝偑偨傢傫偩応崌偵丄偦偺巟揰忋偱夞揮偡傞偙偲傕壜擻偱偡丅
丂夞揮巟揰偼丄巟揰偱夞揮偩偗偼壜擻偱偁傞偑丄
丂悈暯曽岦偵傕墧捈曽岦偵傕堏摦偑偱偒側偄丅
丂峔憿忋偼巟揰偵僺儞傪擖傟偨傕偺偲峫偊傑偡丅
丂屌掕巟揰偼丄偼傝偺抂傪懠偺峔憿暔偵杽傔崬傫偩傛偆側峔憿偵側偭偰偍傝丄
丂偼傝偺堏摦偼傕偪傠傫丄夞揮偺偱偒側偄傛偆偵屌掕偝傟偰偄傑偡丅
4.5.3丂椡偺偮傝崌偄忦審
丂椡偺嶌梡偺傕偲偱丄暔懱偑堏摦媦傃夞揮傪婲偝側偄忬懺偵偁傞偲偒丄
丂偦偺暔懱偼偮傝崌偄忬懺偵偁傞偲偄偆丅
丂傑偨丄偦偺偲偒偺椡偼偮傝崌偭偰偄傞偲偄偆丅
丂偮傑傝丄宯慡懱偵嶌梡偡傞擟堄曽岦偺椡媦傃擟堄偺揰偺傑傢傝偺儌乕儊儞僩偺榓偑丄
丂侽偱偁傞偙偲傪堄枴偟偰偄傑偡丅
丂悈暯曽岦偺椡偺偮傝崌偄傪儼俫亖侽偲昞偟丄
丂墧捈曽岦偺椡偺偮傝崌偄傪儼倁亖侽偲昞偡丅
丂偦偟偰丄夞揮偺偮傝崌偄傪儼俵亖侽偲昞偡丅俵偼儌乕儊儞僩傪昞偡丅
丂儌乕儊儞僩偲偼丄夞揮偺嫮偝傪昞偡検偱偁傝丄椡亊嫍棧偺師尦傪傕偮丅
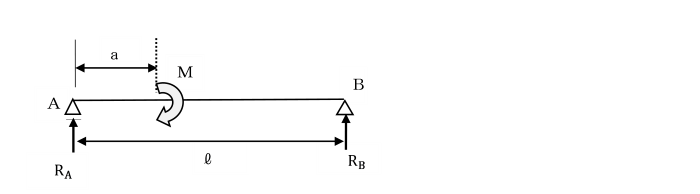
丂椺偊偽丄挿偝俁l偺斅傪仮宆偺巟揰偵恾偺傛偆偵嵹偣傑偡丅
丂偙偺偲偒斅偺嵍抂偵墧捈壓岦偒偺壸廳俹1傪偐偗丄
丂塃抂偵墧捈壓岦偒偺壸廳俹2傪偐偗傑偡丅
丂巟揰埵抲仮偵懳偟偰丄巟揰嵍懁偺俹1偼斀帪寁夞傝偺夞揮傪婲偦偆偲偟傑偡丅
丂偙偺偲偒嵍懁偐傜偺俹1偵傛傞夞揮岠壥偼俹1丒l偲側傝丄
丂塃抂偐傜偺俹2偵傛傞帪寁夞傝偺夞揮岠壥偼丄俹2丒俀l亖俀俹2丒l偲側傝傑偡丅
丂偙偺夞揮岠壥傪儌乕儊儞僩偲偄偆丅
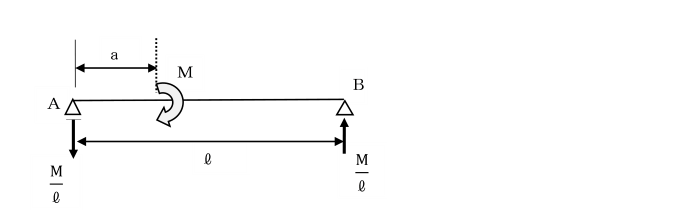
丂俹1丒l亖俀俹2丒l乮偮傑傝丄俹1=俀俹2乯偱偁傟偽丄巟揰埵抲仮偵偍偄偰丄
丂嵍懁偐傜偺斀帪寁夞傝偺夞揮偲丄塃懁偐傜偺帪寁夞傝偺夞揮偑偮傝崌偭偰嬒峵偟丄
丂斅偼偳偪傜偵傕夞揮偟側偄丅偙傟偑丄儌乕儊儞僩偑偮傝崌偭偰偄傞忬懺偱偡丅
4.5.4丂巟揰斀椡媦傃抐柺椡偺寁嶼
椡偺偮傝崌偄忦審偺揔梡庤弴
4.5.5 抐柺椡偺晞崋
嘥 嬋偘儌乕儊儞僩恾偺尒曽偲栺懇
嘥.丂嬋偘儌乕儊儞僩恾偺尒曽偲栺懇
丂偼傝偵奜椡偑嶌梡偡傞偲曄宍偑惗偠傑偡丅
丂偼傝撪晹偵偼曄宍偵掞峈偟丄偼傝偺宍忬傪曐帩偟傛偆偲偡傞撪椡偑敪惗偟傑偡丅
丂晹嵽偵壸廳偑嶌梡偡傞偙偲偵傛偭偰丄
丂嬋偘儌乕儊儞僩偑敪惗偟傑偡丅
丂嬋偘儌乕儊儞僩恾偼丄
丂晹嵽偺偳偺埵抲偵丄偳偺偔傜偄偺嬋偘儌乕儊儞僩偑敪惗偟偰偄傞偐傪恾帵偟偨傕偺偱偡丅
丂嬋偘儌乕儊儞僩恾傪昤偔偵偼栺懇偑偁傝傑偡丅
丂偦傟偼丄嬋偘儌乕儊儞僩恾偼堷挘偺敪惗偡傞懁偵昤偔偲偄偆尨懃偱偡丅
丂嬋偘儌乕儊儞僩恾傪尒傟偽丄偍偍傛偦偺曄宍偺忬嫷傪梕堈偵憐憸偡傞偙偲偑偱偒傑偡丅
丂偙偙偱丄嬋偘儌乕儊儞僩偺惓丒晧偵偮偄偰愢柧偟傑偟傚偆丅
丂嬋偘偺惓丒晧偵偼俀偮偺掕媊偑偁傝傑偡丅
丂1偮栚偼丄塃夞傝偺嬋偘乮帪寁夞傝偺嬋偘乯傪惓丄
丂嵍夞傝偺嬋偘乮斀帪寁夞傝乯傪晧偲偟傑偡丅
丂偙傟偼椡偺偮傝崌偄傪榑偠傞応崌偵梡偄傜傟傞傕偺偱偡丅
丂俀偮栚偼丄壓懁堷挘偺嬋偘傪惓偺嬋偘丄忋懁堷挘偺嬋偘傪晧偺嬋偘偲偟傑偡丅
丂偙偺掕媊偵偟偨偑偊偽丄惓偺嬋偘偼幉慄偺壓懁偵昤偐傟丄
丂晧偺嬋偘偼忋懁偵昤偐傟傑偡丅
丂偙傟偼丄峔憿暔偺曄宍乮嬋偘乯偺忬懺傪棟夝偡傞偨傔偺傕偺偱偡丅
丂偟偨偑偭偰丄嬋偘儌乕儊儞僩傪媮傔傞応崌偼丄曄宍乮嬋偘乯偺忬懺傪棟夝偡傞偨傔偺傕偺偱偁傞偐傜丄
丂俀偮栚偺掕媊傪揔梡偟傑偡丅
丂偦偺媮傔曽偼丄偦偺抐柺偺嵍傑偨偼塃懁偵嶌梡偡傞奜椡偺丄
丂偦偺抐柺偵懳偡傞儌乕儊儞僩偺戙悢榓偱媮傔傜傟傑偡丅
丂壓懁堷挘偺嬋偘偑惓偱偡偐傜丄抐柺偺嵍懁傪峫偊偨帪偼丄帪寁夞傝傪惓乮亄乯丄
丂斀帪寁夞傝傪晧乮亅乯偲偟傑偡丅抐柺偺塃懁傪峫偊偨帪偼丄
丂斀帪寁夞傝偑惓乮亄乯丄帪寁夞傝偑晧乮亅乯偲側傝傑偡丅
丂壓恾偺傛偆偵嵍偐傜侾/俁偺埵抲偵偁傞巟帩揰仮偵偍偄偰偼丄
丂斀帪寁夞傝偺嬋偘儌乕儊儞僩俹1丒l偲帪寁夞傝偺2俹2丒l偑偮傝崌偭偰偄傞傕偺偲偟傑偡丅
丂偙偺応崌偺嬋偘儌乕儊儞僩恾乮俵恾乯傪帵偣偽丄
丂堷挘懁傪幉慄偺忋懁偵昤偔偨傔丄恾偺傛偆偵側傝傑偡丅
丂偙偺応崌偼丄壸廳偐傜棧傟傞傎偳嬋偘儌乕儊儞僩偑戝偒偔側偭偰偄傞條巕傪昞偟偰偄傑偡丅
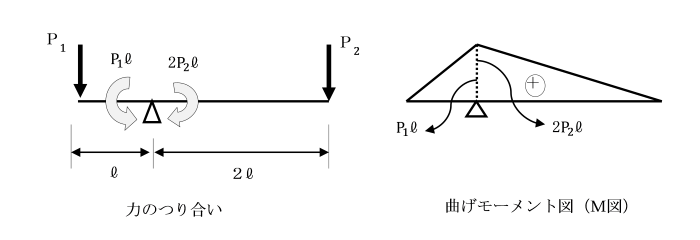
嬋偘儌乕儊儞僩
(a)晞崋婯栺丗
丂嬋偘儌乕儊儞僩偼抐柺傪夞揮偝偣傞摥偒傪帩偪丄
丂夞揮偵傛傝丄壓懁堷挘偺嬋偘傪惓偺嬋偘偲偟傑偡丅
丂晹嵽撪晹偺俙揰偵偍偗傞撪椡宯偺偮傝崌偄偑丄
丂壓恾偺傛偆側忬懺偵側傞偲偒偺嬋偘墳椡乮俵乯偼丄晹嵽偑壓岦偒偵撌偵側傞傛偆偵嶌梡偟傑偡丅
丂偙偺傛偆側嬋偘墳椡傪惓偺晞崋偱昞偡丅
(b)寁嶼婯懃
丂1丏偁傞抐柺偺嬋偘儌乕儊儞僩俵偼丄
丂丂偦偺抐柺傛傝傕嵍懁偵偍偄偰丄
丂丂偼傝偵嶌梡偡傞帪寁夞傝傪惓偲偡傞奜椡儌乕儊儞僩偺戙悢榓偱偡丅
丂2丏偁傞抐柺偺嬋偘儌乕儊儞僩俵偼丄
丂丂偦偺抐柺傛傝傕塃懁偵偍偄偰丄
丂丂偼傝偵嶌梡偡傞斀帪寁夞傝傪惓偲偡傞奜椡儌乕儊儞僩偺戙悢榓偱偡丅
嘦 偣傫抐椡恾偺尒曽偲栺懇
丂偣傫抐椡偲偼挿曽宍傪暯峴巐曈宍偵丄
丂惓曽宍傪傂偟宍偵備偑傑偣傞傛偆側椡偱偡丅
丂椺偊偽丄恾偺傛偆偵偼傝偺搑拞偵墧捈廤拞壸廳俹偺嶌梡偡傞扨弮偽傝偼丄
丂墧捈曽岦斀椡偼俼A丄俼B偲側傝傑偡丅
丂偣傫抐椡恾偼丄墧捈曽岦斀椡偲墧捈曽岦壸廳偐傜媮傔傞偙偲偑偱偒傑偡丅
丂偣傫抐椡恾傪帵偣偽丄恾偺傛偆偵側傝傑偡丅
丂偣傫抐椡恾傪昤偔応崌丄傑偢嵍抂俙揰偵偍偄偰丄
丂斀椡偺戝偒偝偲岦偒傪偦偺傑傑俼A傪昤偔丅
丂斀椡偼墧捈忋岦偒側偺偱丄偼傝幉慄偺忋懁偵昤偐傟傑偡丅
丂偦偟偰丄壸廳偑壛傢傞埵抲傑偱悈暯偵怢偽偡丅
丂偮傑傝丄搑拞偵壸廳偑壛傢傜側偄尷傝丄偣傫抐椡偼曄壔偟側偄丅
丂壸廳嶌梡揰偵摓払偡傟偽丄墧捈壓岦偒偵丄壸廳偺戝偒偝暘俹偩偗丄偣傫抐椡傪壓偡丅
丂塃抂俛揰傑偱丄壸廳傕斀椡傕懚嵼偟偰偄側偄偺偱丄偦偺傑傑悈暯偵怢偽偡丅
丂寢壥偲偟偰丄塃抂偺偣傫抐椡恾偼丄俛揰偺斀椡傪昞偟偰偄傑偡丅
丂偮傑傝丄偣傫抐椡恾偺椉抂偼丄墧捈曽岦斀椡傪昞偟偰偄傑偡丅
丂偣傫抐椡偺媮傔曽偼丄偁傞抐柺偺嵍傑偨偼塃懁偵嶌梡偡傞奜椡偺丄
丂偦偺抐柺偺墧捈曽岦偺暘椡偺戙悢榓偱偡丅
丂惓偺偣傫抐椡傪庴偗傞偲丄嵍偺柺偼帩偪忋偘傜傟偰塃偺柺偼壓偘傜傟偰丄
丂偣傫抐曄宍偟傑偡丅
丂偟偨偑偭偰丄抐柺偺嵍懁傪峫偊偨帪偼丄
丂奜椡偑忋岦偒偺帪偑惓乮亄乯丄壓岦偒偺帪偑晧乮亅乯偲側傝傑偡丅
丂傑偨丄塃懁傪峫偊偨帪偼丄奜椡偑壓岦偒偺帪偑惓乮亄乯丄忋岦偒偺帪偑晧乮亅乯偲側傝傑偡丅
偣傫抐椡
(a)晞崋婯栺丗
丂偣傫抐椡偼抐柺偺嵍懁偐傜媮傔傞応崌丄
丂奜椡偑忋岦偒偺帪偑惓乮亄乯丄壓岦偒偺帪偑晧乮亅乯偲側傝傑偡丅
丂傑偨丄塃懁傪峫偊偨帪偼丄奜椡偑壓岦偒偺帪偑惓乮亄乯丄
丂忋岦偒偺帪偑晧乮亅乯偲側傝傑偡丅
丂晹嵽撪晹偺俙揰偵偍偗傞撪椡宯偺偮傝崌偄偑丄
丂壓恾偺傛偆側忬懺偵側傞偲偒偺偣傫抐椡乮俽乯偼丄
丂晹嵽傪帪寁夞傝偵夞揮偡傞丅
丂偙偺傛偆側偣傫抐椡傪惓 偺晞崋偱昞偡丅
(b)寁嶼婯懃
丂侾丏偁傞抐柺偺偣傫抐椡俽偼丄偦偺抐柺傛傝傕嵍懁偵偍偄偰丄
丂丂忋岦偒傪惓偲偡傞奜椡偺戙悢榓偱偡丅
丂俀丏偁傞抐柺偺偣傫抐椡俽偼丄偦偺抐柺傛傝傕塃懁偵偍偄偰丄
丂丂壓岦偒傪惓偲偡傞奜椡偺戙悢榓偱偡丅
嘨 幉曽岦椡恾偺尒曽偲栺懇
丂偼傝偵孹幬壸廳側偳偑摥偔応崌丄
丂幉曽岦椡偑惗偠傑偡丅
丂幉曽岦椡偵偼埑弅椡偲堷挘椡偑偁傝傑偡丅
丂幉曽岦椡偼丄擟堄偺抐柺偺嵍懁傑偨偼塃懁偵偁傞幉曽岦偺奜椡偺榓偱丄
丂偦偺晞崋偼丄堷挘椡傪亄丄埑弅椡傪亅偲偟傑偡丅
丂偮傑傝丄抐柺偺嵍懁丄塃懁偺椉曽偵偍偄偰丄
丂奜椡偑墦偞偐傞椡乮堷挘椡乯傪亄丄
丂岦偐偭偰偔傞椡乮埑弅椡乯傪亅偲偟傑偡丅
丂偼傝偺奺揰偺幉曽岦椡傪丄偼傝慡懱偵恾帵偟偨傕偺傪幉曽岦椡恾偲偄偆丅
丂亄偺幉曽岦椡偼婎弨慄偺壓懁偵丄亅偺幉曽岦椡偼忋懁偵昤偔丅
幉曽岦椡
(a)晞崋婯栺丗
丂偁傞抐柺偺幉曽岦椡俶偼丄奜椡偑偦偺抐柺偵墦偞偐傞椡乮堷挘椡乯傪亄丄
丂岦偐偭偰偔傞椡乮埑弅椡乯傪亅偲偟傑偡丅
丂晹嵽撪晹偺俙揰偵偍偗傞撪椡宯偺偮傝崌偄偑丄
丂壓恾偺傛偆側忬懺偵側傞偲偒偺幉曽岦椡乮俶乯偼丄
丂俙揰傪堷挘傞傛偆偵嶌梡偟傑偡丅
丂偙偺傛偆側幉椡傪乽堷挘墳椡乿偲屇傃丄惓 偺晞崋偱昞偡丅
(b)寁嶼婯懃
丂侾丏偁傞抐柺偺幉曽岦椡俶偼丄偦偺抐柺偺嵍懁偵偍偄偰丄
丂丂奜椡偑墦偞偐傞椡乮堷挘椡乯傪惓偲偡傞幉曽岦椡偺戙悢榓偱偡丅
丂俀丏偁傞抐柺偺幉曽岦椡俶偼丄偦偺抐柺偺塃懁偵偍偄偰丄
丂丂奜椡偑墦偞偐傞椡乮堷挘椡乯傪惓偲偡傞幉曽岦椡偺戙悢榓偱偡丅
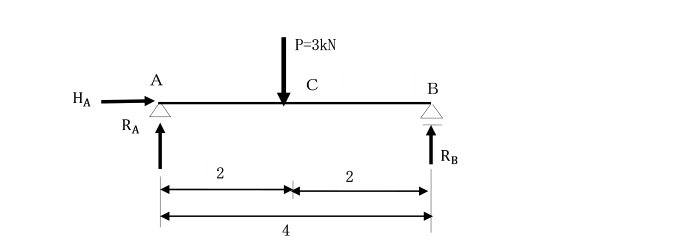
亂椺戣係亅俀亃
丂恾偺傛偆側扨弮偽傝偺巟揰斀椡乮俼A丄俼B丄俫A乯傪寁嶼偟傑偟傚偆丅
亂夝摎係亅俀亃
亂庤弴侾乣係亃
丂壜摦巟揰偲夞揮巟揰偱椉抂傪巟偊偰偄傞偼傝傪扨弮偽傝偲尵偄偄傑偡丅
丂恾偱偼丄偮傝崌偄幃傪棫偰傞偨傔偵丄
丂夞揮巟揰偵偼俼A偲俫A傪壖掕丄
丂壜摦巟揰偵偼俼B傪壖掕偟傑偡丅
丂壖掕偱偁傞偨傔丄巟揰斀椡偺曽岦偼媡偱傕峔傢側偄丅
丂側偍丄壜摦巟揰偼悈暯壸廳傪庴偗帩偮偙偲偼偱偒側偄偨傔丄壖掕偡傞昁梫偼偁傝傑偣傫丅
亂庤弴俆亃
丂儼倁丗俼A亄俼B亅3kN亖侽
丂儼俫丗HA亖侽丂丂偲側傝傑偡丅
丂悈暯壸廳偼嶌梡偟偰側偄偨傔丄俫A偼侽偲側傞丅
亂庤弴俇亃
丂師偵儌乕儊儞僩偵傛傞偮傝崌偄傪峫偊傑偡丅
丂俛揰傪夞揮巟揰偺拞怱偵偟偰丄
丂嵍懁偺壸廳偐傜弴斣偵寁嶼偟傑偡丅
丂俼A偼丄俛揰偐傜傒偰丄帪寁夞傝偵夞揮偡傞傛偆側椡偑摥偒傑偡丅
丂偙傟偼俛揰傪儌乕儊儞僩偺拞怱偵偟偨帪丄
丂僾儔僗乮亄乯偺儌乕儊儞僩偺椡偲側傞偺偱丄
丂亂俼A亊4m亃偲偄偆幃偵側傝傑偡丅
丂偙傟偲摨偠傛偆偵俼A傛傝2m偺埵抲偵偁傞俹偺壸廳傪峫偊傞偲丄
丂斀帪寁夞傝偺儌乕儊儞僩偑嶌梡偡傞椡偵側傞偺偱丄
丂儅僀僫僗乮亅乯婰崋偑偮偄偰亂亅3kN亊2m亃偲側傝傑偡丅
丂夞揮巟揰俛傪儌乕儊儞僩偺拞怱偵峫偊偰偄傞偐傜丄
丂椡偺儌乕儊儞僩偑偮傝崌偭偰偄傞偨傔侽偵側傝傑偡丅
丂偟偨偑偭偰丄
丂儼俵亖俼A亊4m亅3kN亊2m亖侽
丂
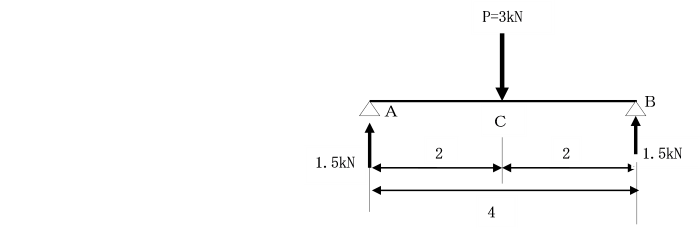
亂庤弴俈乣俋亃
丂傑偢丄椡偺儌乕儊儞僩偺幃傛傝
丂係俼A亖6
丂俼A亖1.5kN
丂偦偟偰丄墧捈曽岦偺椡偺偮傝崌偄幃
丂儼倁丗俼A+俼B亅3亖侽 傛傝丄
丂1.5亄俼B亖3kN
丂俼B亖1.5kN
亂庤弴侾侽亃 嬋偘儌乕儊儞僩偺寁嶼
丂擟堄抐柺偺嬋偘儌乕儊儞僩偼丄
丂偦偺抐柺偺嵍懁傑偨偼塃懁偵嶌梡偡傞奜椡乮巟揰斀椡娷傓乯偺
丂偦偺抐柺偵懳偡傞儌乕儊儞僩偺戙悢榓偱偡丅
丂傑偢丄俙俠娫偺抐柺偵偮偄偰峫偊傞偲丄
丂偙偺抐柺偺嵍懁偵偍偗傞奜椡偼丄巟揰斀椡俼A=1.5kN偺傒偱偡丅
丂峫偊偰偄傞抐柺偐傜俼A傑偱偺嫍棧偼倶偱偡偐傜丄
丂偙偺抐柺偺儌乕儊儞僩俵x亖俼A丒x亖1.5x偱偡丅
丂俵c亖1.5亊2=3kN丒m偲側傝傑偡丅
丂偝傜偵丄俠俛娫偺抐柺偵偮偄偰峫偊傞偲丄
丂抐柺偺嵍懁偼丄奜椡偲偟偰俼A乮忋岦偒乯偲
丂俹乮壓岦偒乯偑奺乆倶媦傃乮倶亅俀乯偺嫍棧偵嶌梡偟偰偄傑偡偐傜丄
丂偙偺抐柺偺儌乕儊儞僩俵x偼丄
丂俵x亖俼A丒倶亅俹乮倶亅俀乯
丂丂亖1.5倶亅3乮倶亅俀乯
丂丂亖亅1.5倶亄6偲側傝傑偡丅
丂俠揰偺嬋偘儌乕儊儞僩偼丄
丂俵c亖亅1.5亊2亄6亖3kN丒倣偲側傝傑偡丅
丂偙傟傜嬋偘儌乕儊儞僩傪嬫娫偛偲偵傑偲傔偰帵偡偲丄
丂俙丂揰丂俵倎亖1.5亊0亖0
丂俙俠娫丂俵(a乣c)亖1.5倶
丂俠丂揰丂俵們亖1.5亊2亖3
丂俠俛娫丂俵(c乣b)亖亅1.5倶亄俇
丂俛丂揰丂俵b亖亅1.5亊4亄6亖0
丂傑偨丄俛俠娫偺抐柺偵偮偄偰丄
丂偦偺抐柺偺塃懁偵偮偄偰峫偊傞偲丄
丂奜椡偼丄巟揰斀椡俼_B亖1.5kN偺傒偱偁傝丄
丂峫偊偰偄傞抐柺偐傜俼B傑偱偺嫍棧偼倶偱偁傞偐傜丄
丂偙偺抐柺偺儌乕儊儞僩俵x偼丄
丂俵x亖俼B丒倶亖1.5倶偱偡丅
丂偙偺傛偆偵丄奜椡偺嶌梡忬懺偵傛傝丄
丂抐柺偺嵍懁丄塃懁偳偪傜偺曽岦傪峫偊傞偐偼丄
丂偦偺抐柺偵懳偡傞儌乕儊儞僩寁嶼偺
丂娙扨側曽偺戙悢榓傪慖傋偽傛偄丅
丂師偵媮傔偨嬋偘儌乕儊儞僩傪恾偵昞偟偰傒傞偲丄
丂壓恾偺傛偆偵側傝傑偡丅
丂偙偺傛偆側恾傪嬋偘儌乕儊儞僩恾丄傑偨偼俵恾偲屇傃傑偡丅
丂嬋偘儌乕儊儞僩恾偱偼丄壓抂堷挘偺嬋偘傪惓偺嬋偘丄
丂忋抂堷挘偺嬋偘傪晧偺嬋偘偲偟傑偡丅
丂偙偺掕媊偵廬偊偽丄惓偺嬋偘偼幉慄偺壓懁偵昤偒丄晧偺嬋偘偼忋懁偵昤偒傑偡丅
丂偙偙偱丄壓恾偺扨弮偽傝傪椺偵丄乽嬋偘偑偮傝崌偆乿偲偄偆偙偲偵偮偄偰峫偊傑偟傚偆丅
丂嵍抂偐傜1倣偺埵抲a-a偱偙偺偼傝傪壖憐揑偵愗傝棧偟偰傒傑偡丅
丂偙偺帪丄愗抐埵抲偺嵍懁偺嬋偘儌乕儊儞僩偼丄
丂巟揰斀椡俼A亖1.5kN偵傛偭偰惗偠傞帪寁夞傝偺嬋偘儌乕儊儞僩偩偗偱偁傝丄
丂1.5kN亊1倣亖1.5kN丒倣偲側傝傑偡丅
丂堦曽丄愗抐埵抲偺塃懁偺嬋偘儌乕儊儞僩偼丄
丂塃抂偺巟揰斀椡俼B亖1.5kN媦傃廤拞壸廳俹亖3kN偵傛偭偰惗偠傞嬋偘儌乕儊儞僩偱偁傝丄
丂巟揰斀椡俼B偼斀帪寁夞傝偵丄
丂俼B亊3倣亖1.5 kN亊3倣亖4.5kN丒倣
丂廤拞壸廳俹偼帪寁夞傝偵丄
丂俹亊1倣亖3 kN亊1倣亖3kN丒倣丂偲側傝傑偡丅
丂偙傟傜傪懌偟崌傢偣傞偲丄
丂斀帪寁夞傝偵1.5 kN丒倣丂偺嬋偘偲側傝傑偡丅
丂偙偺寢壥丄嵍抂偐傜1倣偺埵抲偱偺嬋偘偼丄
丂嵍偐傜帪寁夞傝偵丄1.5kN丒倣
丂塃偐傜斀帪寁夞傝偵丄1.5kN丒倣偲側傝丄
丂嬋偘偑偮傝崌偆偙偲偑妋擣偱偒傑偡丅
丂偙傟偑儼俵亖侽偺堄枴偱偁傝丄嬋偘偑偮傝崌偆偲偄偆偙偲偱偡丅
亂椺戣係亅俁亃
丂恾偺傛偆側扨弮偽傝偺巟揰斀椡乮俼A丄俼B)傪寁嶼偟傑偟傚偆丅
丂乵拞娫揰偵儌乕儊儞僩壸廳俵偑嶌梡偡傞応崌乶
亂夝摎係亅俁亃
亂庤弴侾乣係亃
丂恾偺傛偆偵嵍抂偐傜a偺埵抲偵丄
丂帪寁夞傝偺儌乕儊儞僩壸廳俵偑嶌梡偟偰偄傑偡丅
丂嵍抂偺俙揰偺巟揰斀椡傪墧捈忋岦偒偵俼A偲壖掕偟丄
丂塃抂俛偺巟揰斀椡傕摨條偵忋岦偒偵俼B偲壖掕偟傑偡丅
亂庤弴俆亃俼A亄俼B亖0
亂庤弴俇亃
丂揰俙夞傝偺儌乕儊儞僩偺偮傝崌偄幃傪棫偰傑偡丅
丂乮偮傝崌偄幃偺応崌偼丄帪寁夞傝傪惓丄斀帪寁夞傝傪晧偲偡傞丅乯
丂俛揰偺巟揰斀椡偵傛傞嬋偘丗亅俼Bl
丂 a偺埵抲偵偁傞儌乕儊儞僩壸廳偵傛傞嬋偘丗亄俵
丂儼俵A亖0偱偁傞偺偱丄
丂亅俼Bl亄俵亖0
丂亪丂俼B亖俵/l丂乮壖掕偟偨偲偍傝墧捈忋岦偒乯
亂庤弴俈乣俋亃
丂俼A亄俼B亖0丂傛傝丄
丂俼A亄俵/l亖0丂亪丂丂俼A亖亅俵/l丂乮壖掕偟偨曽岦偲媡偺墧捈壓岦偒乯
丂仸巟揰斀椡偼儌乕儊儞僩壸廳俵偺嶌梡埵抲偵偼塭嬁傪庴偗側偄丅
亂庤弴侾侽亃
丂巟揰斀椡媦傃奜椡傪梡偄偰嬋偘儌乕儊儞僩傪媮傔傑偡丅
丂嬋偘儌乕儊儞僩偺暘晍偼丄
丂0亙x亙a偵偍偄偰丂俵亖亅俵/l倶
丂 a亙x亙l偵偍偄偰丂俵亖亅(俵/l)倶亄俵
丂偟偨偑偭偰丄x亖0偱偼俵亖0丄x亖l偱偼俵亖0丂偱偡丅
丂師偵丄a揰偺嬌嬤朤偺嵍懁乮a-兠乯媦傃塃懁乮a+兠乯偺埵抲偱偺俵傪峫偊傑偡丅
丂兠乮兠亜0乯傪尷傝側偔0偵嬤偯偗偰偄偔偲丄
丂a揰偺嬋偘儌乕儊儞僩偑媮傑傝傑偡丅
丂倶亖a亅兠偺嬋偘儌乕儊儞僩偼丄
丂0亙x亙a偺応崌偺俵亖亅(俵/l)倶丂幃傪梡偄丄
丂兠傪嬌尷傑偱0偵嬤偯偗傞偲丄
丂嵍懁偺嬋偘儌乕儊儞僩偼丄
丂俵(x)亖亅俵/l乮a亅兠乯
丂乻兠仺0乼丂佀丂俵(x)亖亅(俵/l)a
丂傑偨丄倶亖a偺塃懁偱偼丄a亙x亙l偺応崌偺俵亖亅(俵/l)倶亄俵丂幃傪揔梡偟丄
丂俵(x)亖亅(俵/l)乮a+兠乯亄俵
丂乻兠仺0乼 佀丂俵(x)亖亅(俵/l)a亄俵亖俵乮1亅a/l乯偲側傝傑偡丅
丂傛偭偰丄嬋偘儌乕儊儞僩恾乮俵恾乯偼丄壓恾偺傛偆偵側傝傑偡丅
亂庤弴侾侾亃
丂巟揰斀椡乮墧捈曽岦乯媦傃奜椡傪梡偄偰偣傫抐椡傪媮傔傑偡丅
丂巟揰俙偐傜擟堄偺嫍棧倶偵偁傞抐柺傪峫偊丄
丂偦偺抐柺偵偍偗傞偣傫抐椡傪俽x偲偟傑偡丅
丂抐柺偺嵍懁偵偁傞墧捈曽岦偺奜椡偼斀椡俵/l偺傒偱偡丅
丂偟偨偑偭偰丄
俽(A乣B)亖亅俵/l 偲側傝傑偡丅
亂庤弴侾俀亃
丂巟揰斀椡乮悈暯曽岦乯媦傃奜椡傪梡偄偰幉曽岦椡傪媮傔傑偡丅
丂幉曽岦乮悈暯曽岦乯偵摥偔椡偼側偄偨傔丄幉曽岦椡偼惗偠傑偣傫丅
丂俶亖0
亂椺戣係亅係亃
丂恾偺傛偆側扨弮偽傝偺巟揰斀椡乮俼A丄俼B)傪寁嶼偟傑偟傚偆丅
丂乵椉抂偵儌乕儊儞僩壸廳俵偑嶌梡偡傞応崌乶
亂夝摎係亅係亃
丂椉抂偵儌乕儊儞僩壸廳偑嶌梡偡傞偼傝偼丄
丂嵍抂偁傞偄偼丄塃抂偺傒偵夞揮偺岦偒偑堎側傞儌乕儊儞僩壸廳偑
丂嶌梡偡傞偲偒偺忬懺傪廳偹崌傢偣偨傕偺偲峫偊傜傟傑偡丅
丂偙偺偲偒丄巟揰斀椡偼偦傟偧傟憡嶦偝傟丄
丂椉抂偲傕偵侽偵側傞丅
丂偟偨偑偭偰丄偙偺応崌偺偣傫抐椡偼侽偲側傝傑偡丅
丂傑偨丄嬋偘儌乕儊儞僩恾偼俙揰偐傜俛揰傑偱堦掕偱俵偲側傝傑偡丅
丂2偮偺奜椡偲偟偰偺儌乕儊儞僩壸廳俵偼丄
丂戝偒偝偑摍偟偔岦偒偑斀懳偱偁傞偨傔丄
丂奜椡摨巑偱偮傝崌偭偰偄傞忬懺偱偡丅
丂偟偨偑偭偰丄巟揰斀椡偑惗偠傑偣傫丅
亂椺戣係亅俆亃
丂恾偺傛偆側曅帩偪偽傝偺帺桼抂俛偵儌乕儊儞僩壸廳俵偑嶌梡偟偰偄傞応崌偺巟揰斀椡俼A傪媮傔傛丅
丂傑偨丄嬋偘儌乕儊儞僩恾傪昤偗
亂夝摎係亅俆亃
亂庤弴侾乣係亃
丂恾偺傛偆偵俙揰偺巟揰斀椡傪墧捈忋岦偒偵俼A丄
丂悈暯斀椡傪塃岦偒偵俫A丄
丂嬋偘儌乕儊儞僩傪斀帪寁夞傝偵俵A偲壖掕偟傑偡丅
亂庤弴俆亃
丂儼俫亖0丂丂俫A亖0
丂儼倁亖0丂丂俼A亖0
亂庤弴俇亃
丂俙揰偺夞傝偺儌乕儊儞僩傪峫偊傑偡丅
丂儼俵亖0
丂亅俵A亄俵亖0丂丂亪俵亖俵A
亂庤弴俈亃
丂巟揰斀椡丂俼A亖0丂, 俫A亖0丂,嬋偘儌乕儊儞僩俵A亖俵丂丂偲側傝傑偡丅
丂偙偙偱丄曅帩偪偽傝傪擟堄偺揰俠偱壖憐揑偵愗抐偟丄
丂偦偺塃懁偵偍偄偰丄椡偺偮傝崌偄傪峫偊傑偡丅
丂俠揰偺夞傝偺儌乕儊儞僩偼丄
丂亅俵C亄俵亖0丂丂亪丂俵C亖俵
丂擟堄偺俠揰傪偳偙偵偲偭偰傕
丂俵C亖俵丂偱堦掕偲側傝傑偡丅
丂傑偨丄壖憐愗抐偟偨俠俛晹嵽偺曄宍忬懺偼丄
丂忋懁偑堷挘偲側傞偺偱丄嬋偘儌乕儊儞僩偼晧偲側傝傑偡丅
僩僢僾儁乕僕