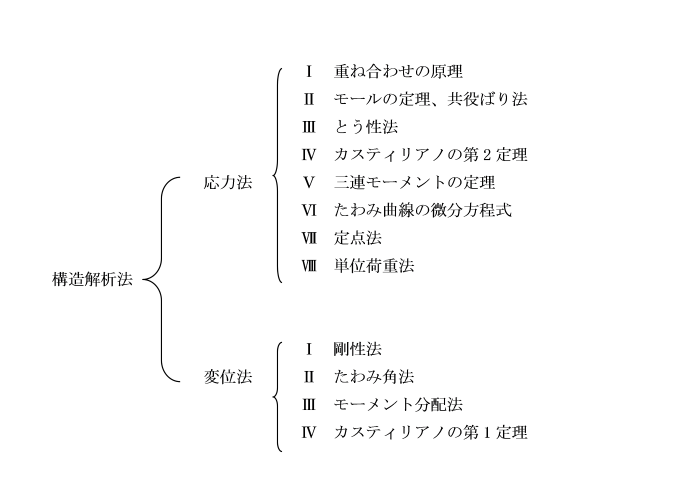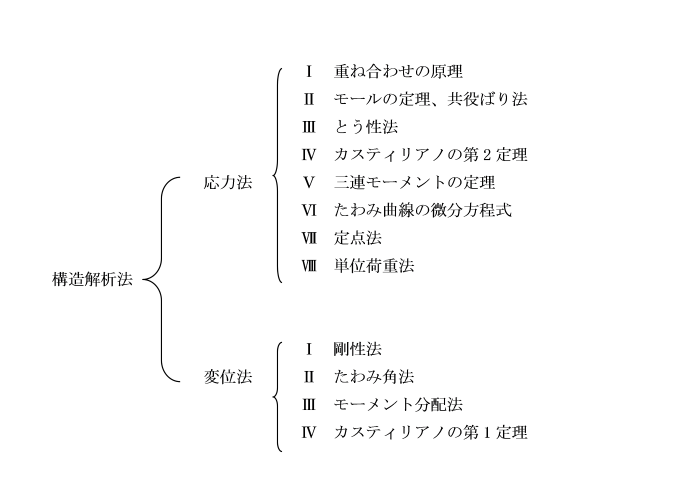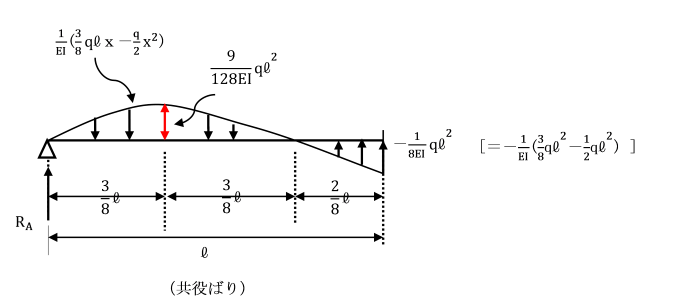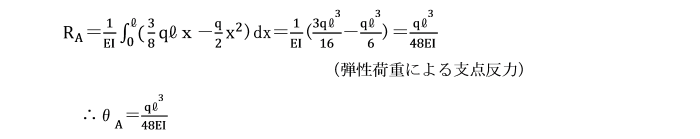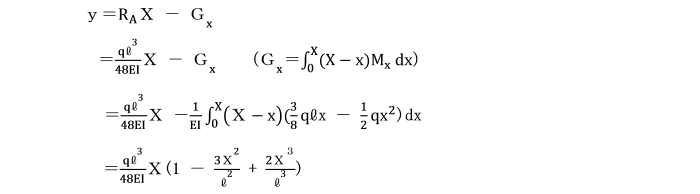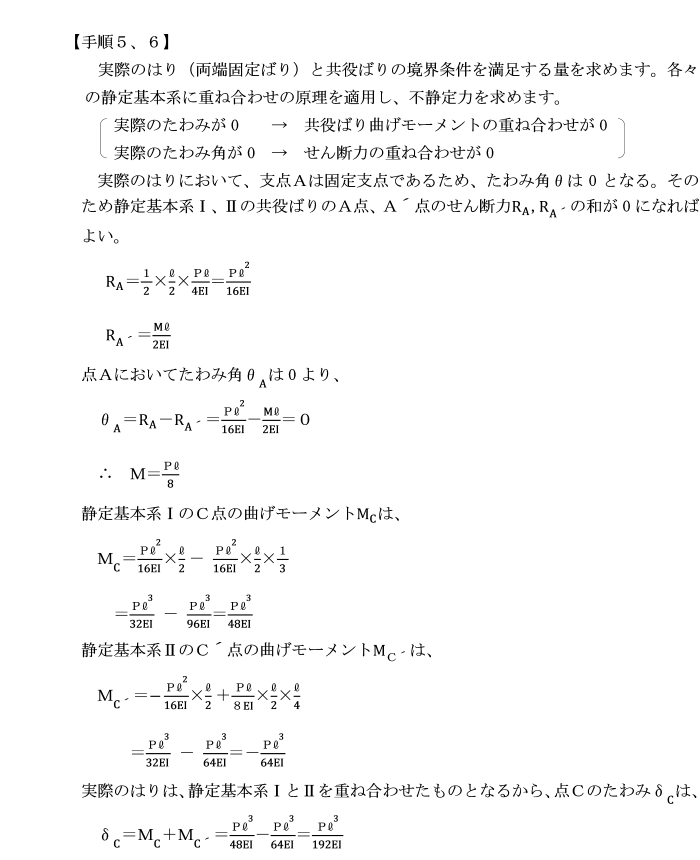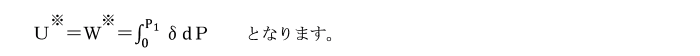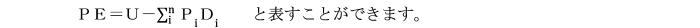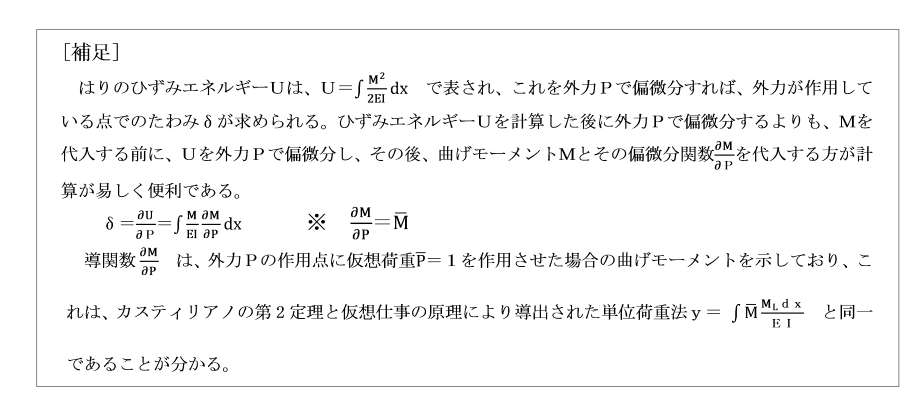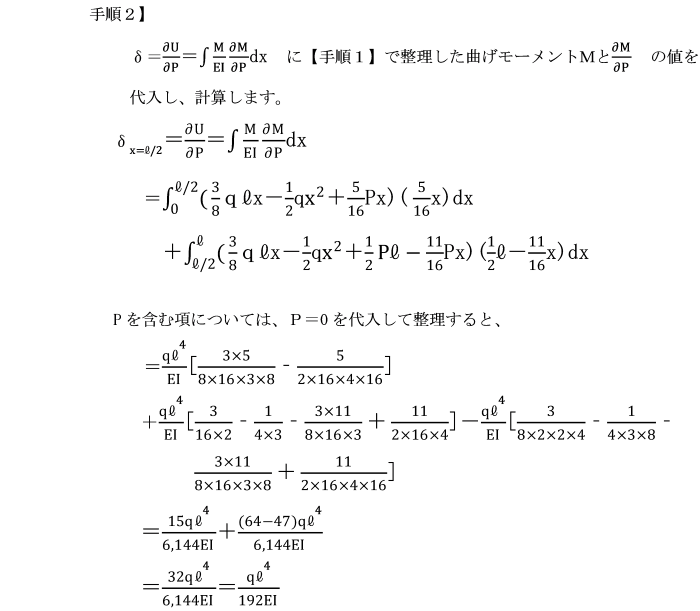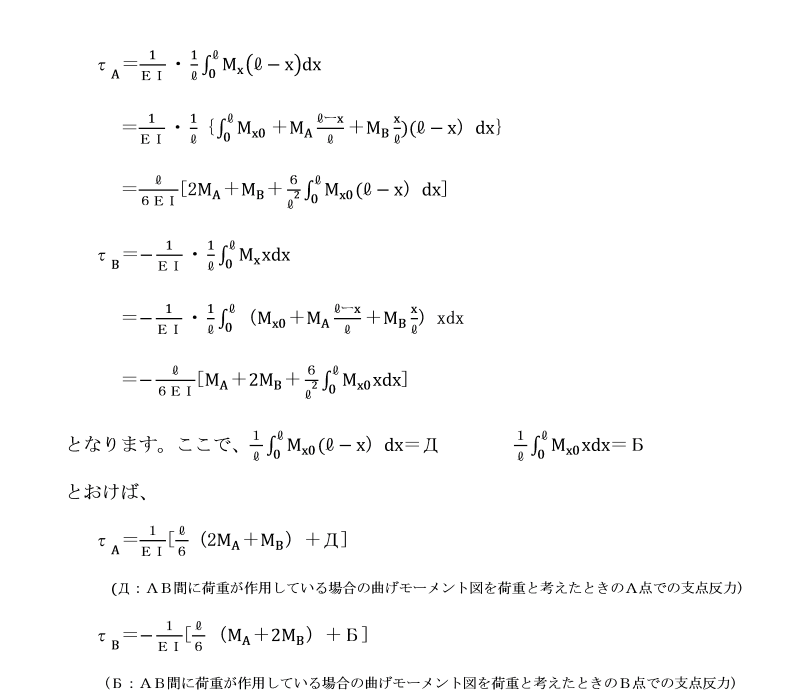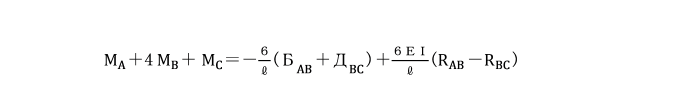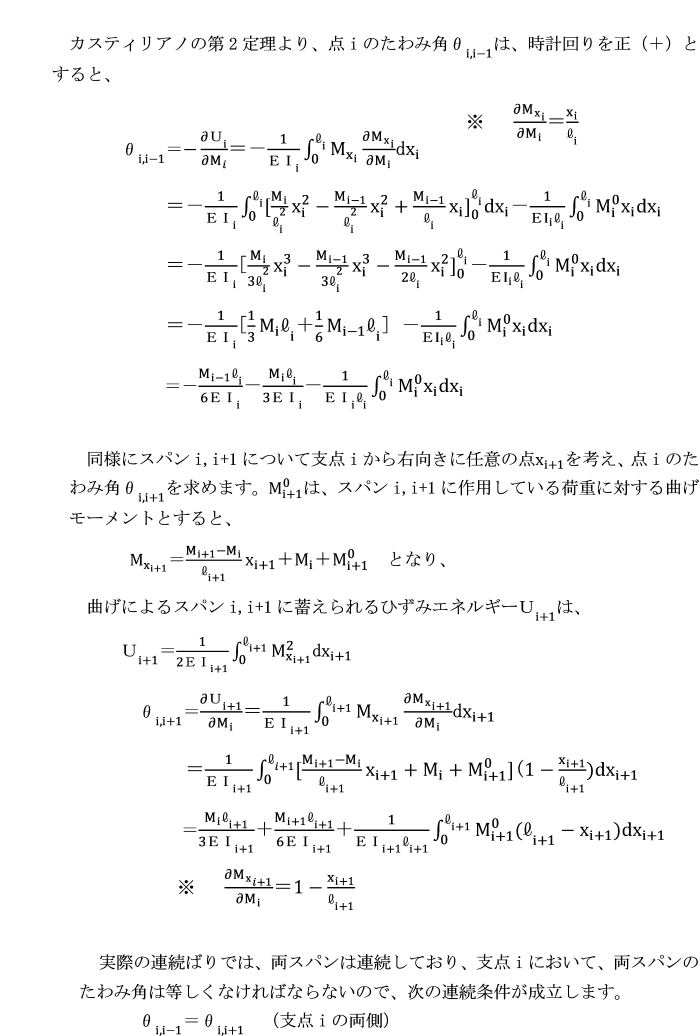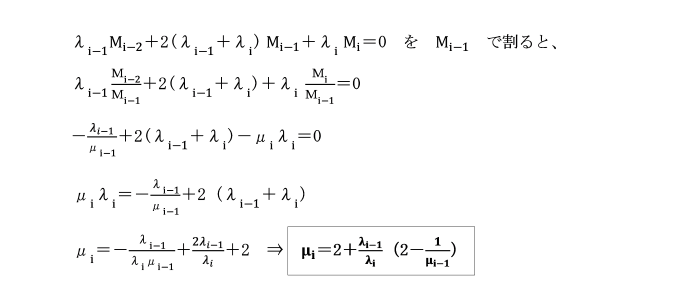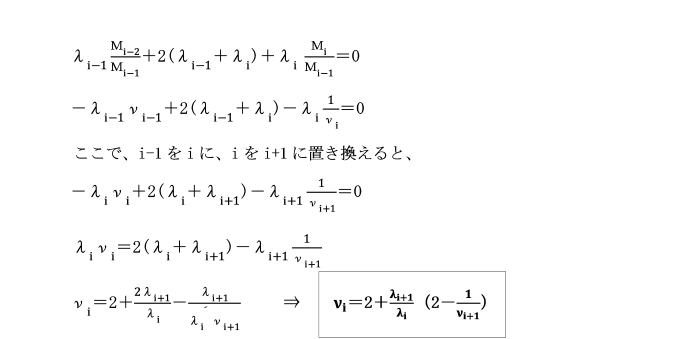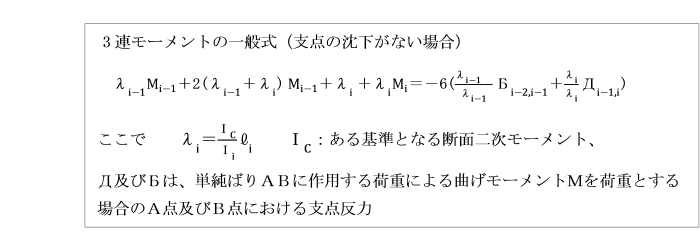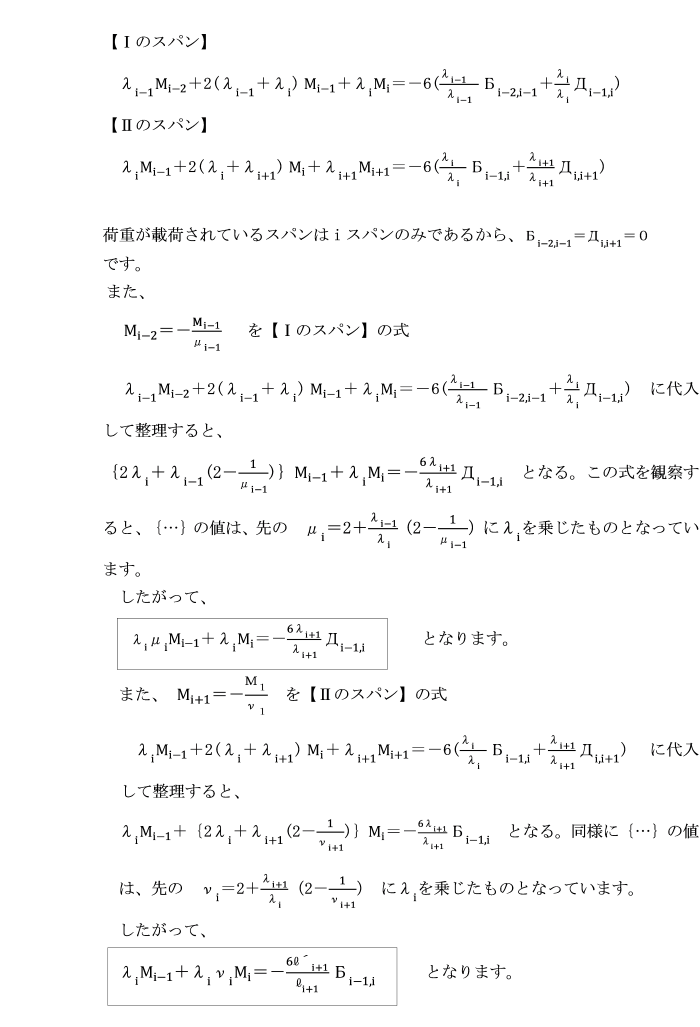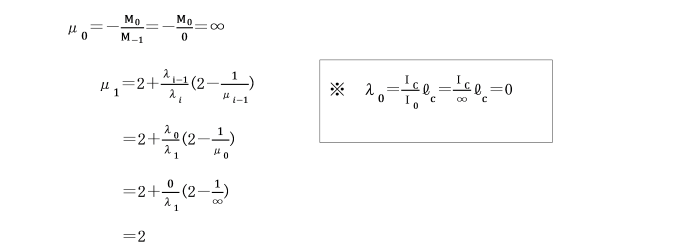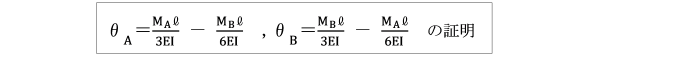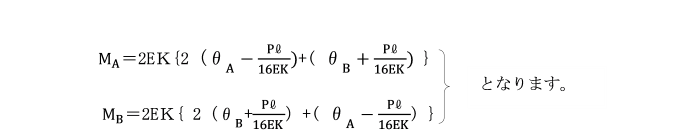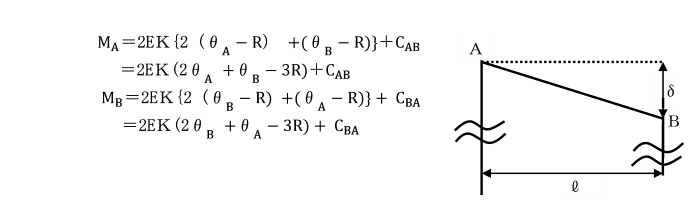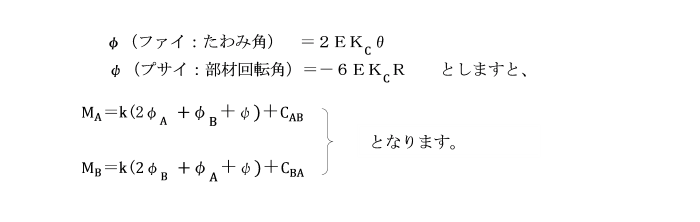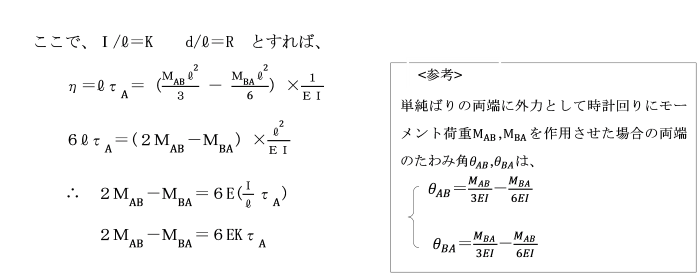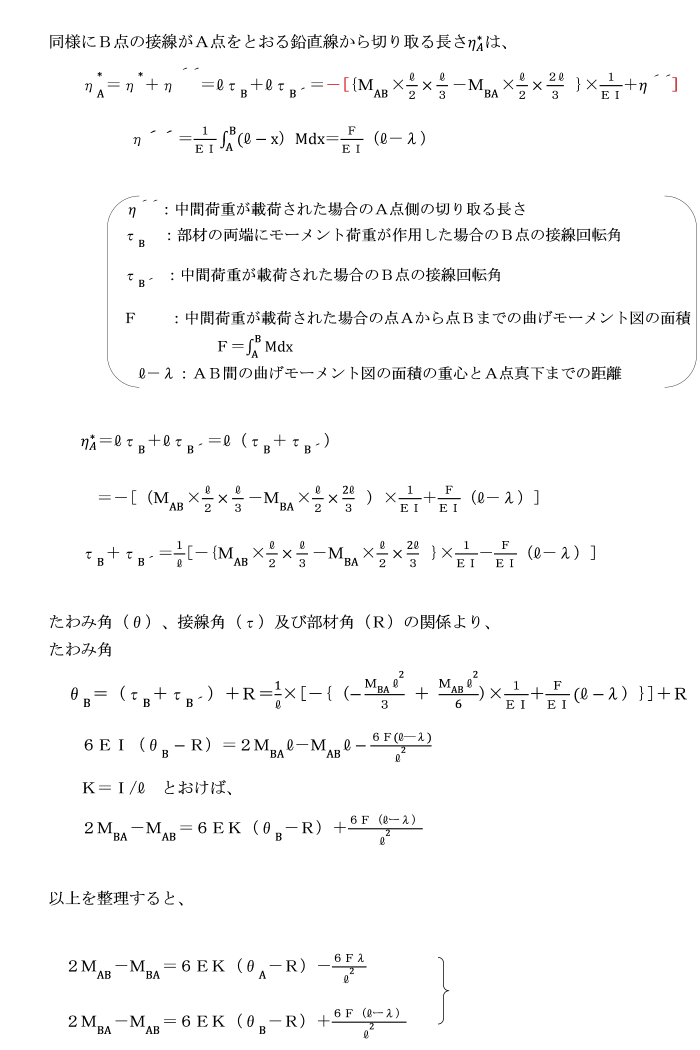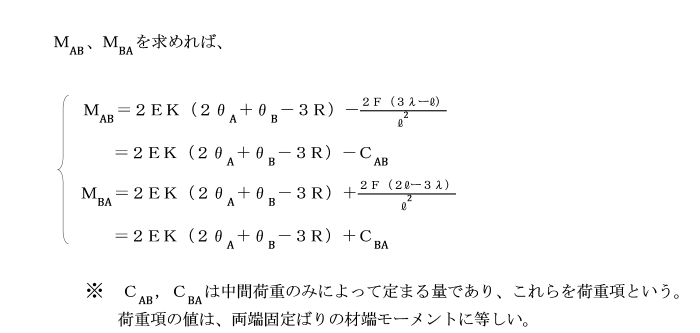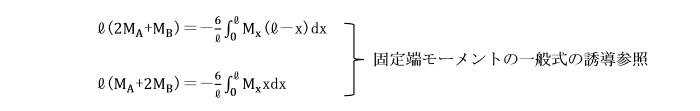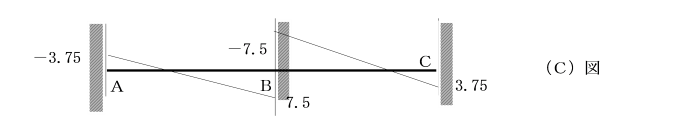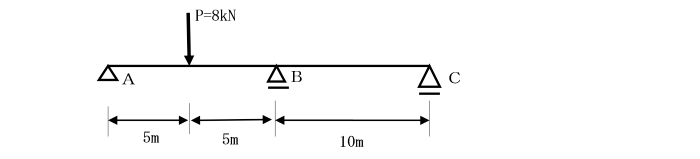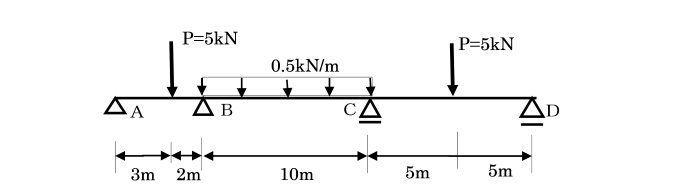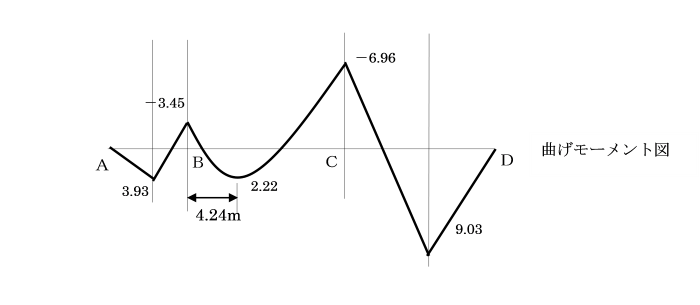トップページ
第8章 構造解析法への適用
8.1 構造解析の目的
構造物が荷重、温度変化、支点の沈下などの作用を受けると、
部材内部には断面力が生じます。
また、部材各部には変形、変位が生じます。
構造解析は、これらを求め、
構造物が力学的に安全かどうか検討することです。
※ 変形:着目している物体の形が変わることを意味します。
※ 変位:着目している点がどこに移動したかを意味します。
8.2 応力法と変位法
構造物の反力、断面力及び変位を求める手法として、
未知量を支点反力や断面力をとる応力法と
支点や節点のたわみやたわみ角を介して支点反力や断面力を求める変位法の二つの解法があります。
8.2.1 応力法の特徴
未知量を支点反力や断面力とし、
境界条件や連続条件を用い、直接支点反力や断面力を決定する方法です。
静定構造物では、力のつり合い条件式のみで支点反力や断面力が決定できます。
不静定構造物では、不静定力の選び方など工夫が必要で、コンピュータ解析には適していません。
8.2.2 変位法の特徴
未知量を支点や節点のたわみやたわみ角とし、
境界条件や連続条件を用い、
支点反力や断面力を間接的に求める方法です。
未知量が多くなりますが、
機械的に求められ、コンピュータの解析に適しています。
骨組構造(細長い棒状の部材を組み立てた構造物)に対して用いられています。
8.3 構造解析法の分類
8.4 応力法による解法
不静定ばりの各種解析法の特徴を理解するため、
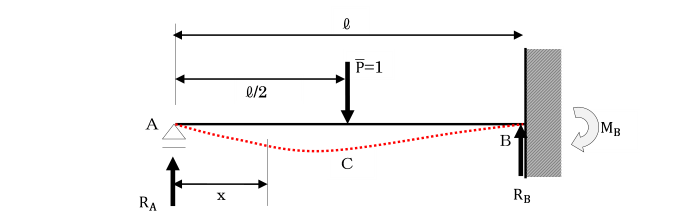
1次の不静定ばりである「枕片持ちばり」を例に、支点反力及び断面力を求めてみましょう。
[各種解析法に適用する構造物(枕片持ちばり)]

8.4.1 重ね合わせの原理
荷重によって生ずる変位、変形量(ひずみ)が微小で、
変形量が荷重の大きさに比例するような構造物を線形構造物といいます。
これに対して、荷重とそれによって構造物に生ずる変形量の間に非線形関係が存在する場合、
その構造物を非線形構造物といいます。
重ね合わせの原理は、外力と変形の間に線形関係が成立する構造物に適用できます。
複数の外力が、構造物に作用したとき、たわみや断面力などは、
一つずつの外力が作用したときのたわみや断面力などを足し合わせたものと等しくなります。
つまり、線形構造物にn個の荷重からなる1組の荷重群が作用したとします。
そのときに生ずる変形量Yは、
個々の荷重Pi(i=1,2,…,n)が
独立して作用したときの変形量Yiをi=1,2,…,nを総和することによって求められます。
不静定ばりを重ね合わせの原理を用いて解く場合、
不静定次数の数だけ支点の拘束を取り除いた静定ばりを考えます。
次にその静定ばりに、拘束を取り除いた部分に、
元の不静定構造物の不静定力を外力として静定ばりに載荷します。
これらの静定ばりが、
実際の不静定ばりの変位の境界条件を満足するように不静定力を求めます。
つまり、静定ばりのたわみ、たわみ角の値を用いて解析する解法です。
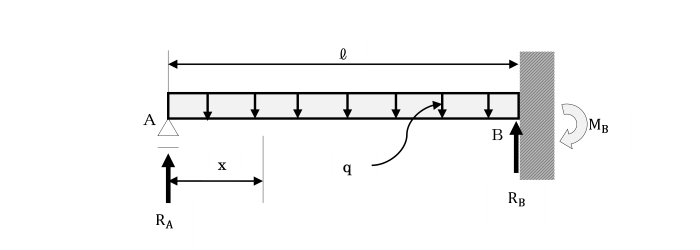
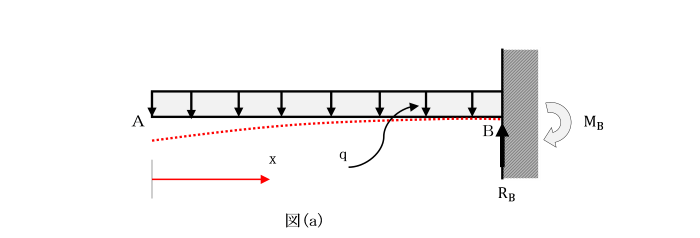
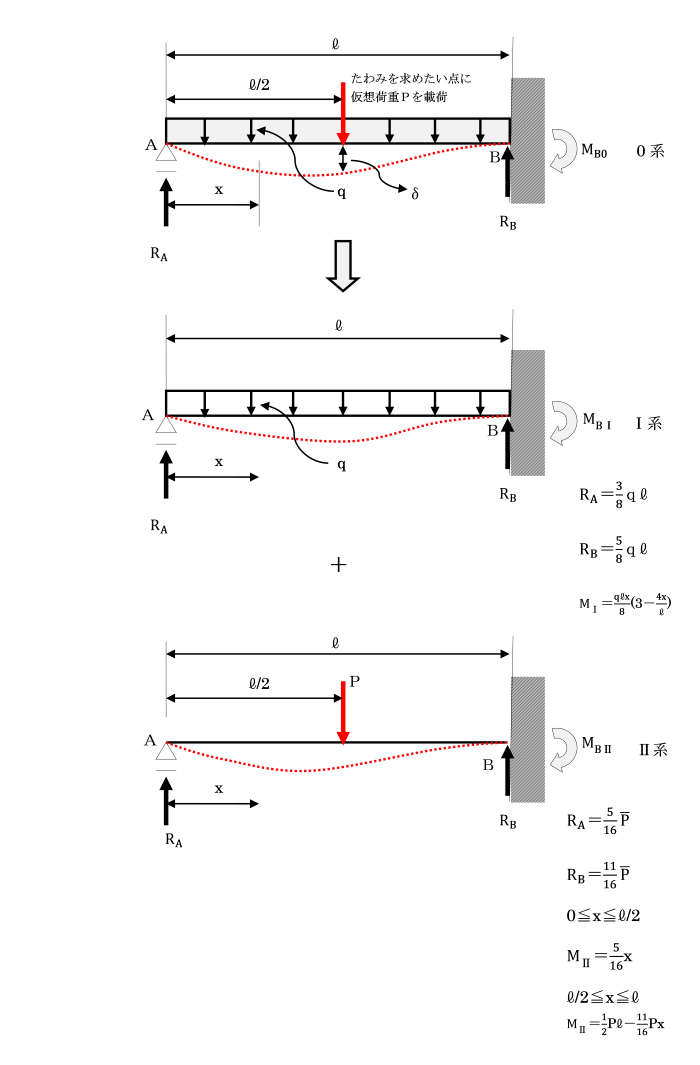
下図の1次の不静定ばりで、
左端の可動支点Aの鉛直方向の拘束を取り除いた静定ばりⅠと、
その左端に元のはりで生じている不静定力RAが作用している静定ばりⅡとを重ね合わせると、
元のはりと等価になります。
【Ⅰ】 重ね合わせの原理により、枕片持ちばりの支点反力及び断面力を求めよ。
[枕片持ちばり:再掲]

[解法の手順]
はりの支点反力や固定支点での曲げモーメントは、
変位の拘束によって生じます。
つまり固定支点Bの反力RBと曲げモーメントMBは、
支点Bのたわみとたわみ角の拘束δBとθBによって生じます。
支点Aの反力RAは、
支点Aのたわみの拘束δA=0によって生じます。
【手順1】
不静定次数の数だけ変位の拘束を解放し、
静定基本系に置き換えます。
支点反力RAを不静定量として選定します。
すると静定基本系は、分布荷重が載荷された片持ちばりとなります。
【手順2】
解放した変位に対応する反力を不静定力RAとして静定基本系に作用させます。
【手順3】
元の不静定ばりの変位の条件を満足させることにより、不静定力を求めます。
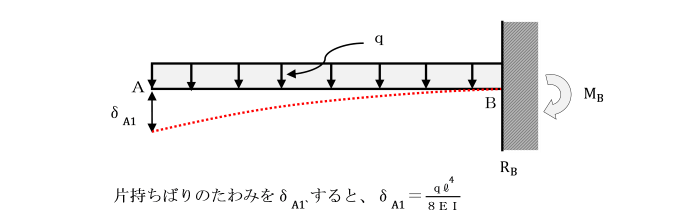
不静定力RAに対するたわみをδA2とします。
δA2=-RAl3/3EI
実際、支点Aは拘束されていますから、
たわみδA1及びδA2の重ね合わせから構造物の全たわみδAは、
δA=δA1+δA2=0
δA=ql4/8EI -RA l3/3EI=0 ⇒ RA l3/3=ql4/8 ∴ RA=3ql/8
【手順4】
不静定力が求まれば、つり合い条件式により、
残りの支点反力、断面力を境界条件、連続条件を用いて決定します。
RA+RB=ql より、 RB=ql-3ql/8=5ql/8
また、点Bの曲げモーメントMBは、
MB=3ql2/8- ql×1/2=-ql2/8
曲げモーメントの一般式Mxは、
Mx=RA・x-q・x2/2=3qlx/8-qx2/2 となります。
8.4.2 たわみ曲線の微分方程式による解法
荷重によって変形したはりの軸が示す曲線を弾性曲線と呼びます。
変形前の軸上の点は、変形後その位置が移動します。
その移動した距離の鉛直方向の射影をたわみといいます。
はりが変形したために、
実際は水平方向にx、鉛直方向にyの変位を生じます。
B点はB´点に、C点はC´点に移動しますが、
その移動したC´点の鉛直方向の射影距離yをC点の鉛直方向にプロットします。
このように任意点から鉛直方向に射影距離をプロットして描かれた曲線をたわみ曲線といいます。
しかし、実際には、曲げ変形に伴う水平変位xは、
微小ですので変形曲線は、鉛直変位yだけで表してかまいません。
そのため弾性曲線をたわみ曲線といっても実用上差し支えありません。
たわみ曲線の微分方程式は、次のように表されます。
d2y/dx2=-M/EI (y:たわみ、x:断面の位置、M:曲げモーメント、EI:曲げ剛性)
(解法の手順)
たわみ角は1回積分して、dy/dx=θ=-∫M/EIdx+C1
たわみはさらに積分して、y=-∬M/EIdxdx+C1x+C2
積分定数C1,C2は境界条件、連続条件より決定します。
[境界条件]
はりの左端 x=0 右端 x=l において、
・単純支持 y(たわみ)=0 M(曲げモーメント)=0
・固定端支持 y(たわみ)=0 θ(たわみ角)=0
・自由端 S(せん断力)=0 M(曲げモーメント)=0
[連続条件]
例えば、単純ばりに集中荷重が x=a の位置に作用している場合、x=aでは、
y1=y2 (たわみ)
θ1=θ2 (たわみ角)
S1=S2 (せん断力)
M1=M2 (曲げモーメント)
【Ⅱ】 たわみ曲線の微分方程式により、枕片持ちばりの支点反力、断面力を求めよ
[枕片持ちばり:再掲]

[解法の手順]
(静定基本系)
図の不静定構造物から不静定次数に等しい個数の不静定反力を取り除くと、
静定構造物が得られます。
これを元の不静定構造物の静定基本系といいます。
<不静定次数>
n=m+r+p-2k=1+4+0-2×2=1
∴ 1次不静定構造物
n:不静定次数 m:部材数 r:反力数
p:剛節接合材数 k:節点数
ここではRAを不静定力とします。
EI・d2y/dx2=-Mx=-(RA・x-1/2・qx2)
EI・dy/dx=-RA・x2/2+qx3/6 + C1
EIy=-RA・x3/6+qx4/24 + C1・x + C2
境界条件
x=0 のとき y=0 ⇒ C2=0
x=l のときθ=0
0=-RAl2/2+ql3/6 + C1 ⇒ C1=RAl2/2 - ql3/6
x=l のときy=0
0=-RAl3/6 + ql4/24 + C1l
0=-RAl3/6 + ql4/24 + RAl3/2 - ql4/6
-4RA+ql+12RA-4ql=0 ⇒ RA=3ql/8
ql=RA+RB より、
RB=ql-RA=ql-3ql/8 =5ql/8
曲げモーメントの一般式Mx
Mx=3qlx/8 -qx2/2
8.4.3 モールの定理(モーメント面積法)、共役ばり法
モールの定理は、共役(きょうやく)ばりと呼ばれる仮想的なはりに、
曲げモーメントMを曲げ剛性(EI)で割ったM/EIを分布荷重と考え載荷します。
M/EIを弾性荷重といい、弾性荷重法ともいわれます。
この弾性荷重による任意の点のせん断力、曲げモーメントが、
それぞれその点でのたわみ角、たわみに一致するという定理です。
この方法は、はり全体のたわみ曲線を求めるのではなく、
はりの任意の点のたわみ、たわみ角を求める場合に適しています。
[モールの定理]
第1定理:
2点A及びBにおけるたわみ曲線への接線の間の角θは、
これらの2点間の曲げモーメント図の面積を曲げ剛性(EI)で割ったものに等しい。
第2定理:
たわみ曲線上の任意の2点からの接線が、
そのうちの1点をとおる鉛直線から切り取る長さは、
2点間の曲げモーメント図の面積のその鉛直線をとおる1点に対する断面1次モーメントを
曲げ剛性(EI)で割ったものに等しい。
第3定理:
単純ばりの任意点におけるたわみ角は、
曲げモーメント図を荷重と考えたときの、
その点に生ずるせん断力を曲げ剛性(EI)で割ったものに等しい。
第4定理:
単純ばりの任意点におけるたわみは、
曲げモーメント図を荷重と考えたときの、
その点に生ずる曲げモーメントを曲げ剛性(EI)で割ったものに等しい。
ここで注意すべき点は、第1、第2定理は、
単純ばりにも片持ちばりにも適用できますが、
第3、第4定理は、単純ばりに限定して用いられます。
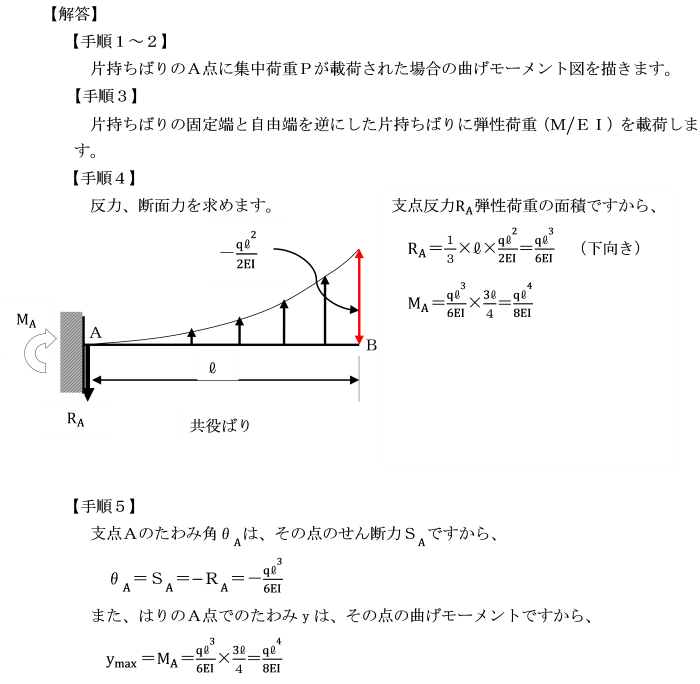
第3、第4定理を片持ちばりに適用する場合は、
その固定端、自由端を逆にした片持ちばりに、
弾性荷重(M/EI)を載荷させなければなりません。
その他のはりに適用するには、
後に説明します「共役ばり法」(片持ちばりも含まれる)を用いる必要があります。
まず、モールの定理の考え方を理解するため、
曲げ部材のつり合い条件式及びたわみ曲線の微分方程式を対比してみましょう。
つり合い条件式:dS/dx=-q 、dM/dx=S または d2 M/dx2 =-q
(q:分布荷重、 S:せん断力、 M:曲げモーメント)
たわみ曲線の微分方程式:d2 y/dx2=-Mx/EI
(y:たわみ、x:断面の位置、M:曲げモーメント、EI:曲げ剛性)
つり合い条件式 d2 M/dx2 =-qより
M=-∬qdxdx + C1x + C2 S=-∫qdx + C1
たわみ曲線の微分方程式 d2 y/dx2=-Mx/EIより
y=-∬Mx/EI dxdx + D1x + D2
θ=-∫M/EI・dx + D1 ※tanθ=dy/dx=θ
これらの積分定数(C1、C2、D1、D2)は、
それぞれ境界条件、連続条件によって決定することができます。
たわみy、たわみ角θ求める方法として、
d2 M/dx2=-q をみると、荷重qが載荷されているはりにおいて、
2回積分をすると曲げモーメントMを求めることができます。
同様にd2 y/dx2=-Mx/EIをみると、
Mx/EIを2回積分すると、たわみyを求めることができます。
これらの関係から、d2 M/dx2=-q の分布荷重qの代わりにM/EIに置き換え、
はりに載荷して、曲げモーメント、せん断力を求めると、
これが、たわみy、たわみ角θに対応していることが分かります。
また、これらの積分定数は、
それぞれ境界条件、連続条件によって、決定することができます。
例えば、はりの長さlの単純ばりの境界条件は、両支点において曲げモーメントが0ですから、積分定数C1、C2は、
M(0)=0、M(l)=0です。
また、両支点においてたわみyは0ですから、積分定数D1、D2は、
y(0)=0、y(l)=0です。
次に、片持ちばりについて、
積分定数を定めるための境界条件を比較してみましょう。
はりの長さlの片持ちばりの境界条件は、自由端においてせん断力S、曲げモーメントMが0ですから、
積分定数C1、C2に対しては、
S(0)=0、M(0)=0 となります。
また、固定端において、たわみ角θ、たわみyは0 ですから、積分定数D1、D2は、
θ(l)=0、y(l)=0 となります。

片持ちばりの境界条件を求める場合、
せん断力と曲げモーメントの積分定数C1、C2は、
自由端の境界条件を用います。
これに対し、たわみ角とたわみの積分定数D1、D2は、
固定端の境界条件を用います。
このことより、片持ちばりのたわみ角とたわみは、
せん断力と曲げモーメントを求めるという考え方に立てば、
元の片持ちばりの自由端と固定端を入れ替えた片持ちばりに、
弾性荷重(M/EI)を載荷して、せん断力と曲げモーメントを求めることになります。
このように境界条件を満たすために仮想的に考えられたはりを、
共役ばりといいます。
実際のはりの変位(たわみ角、たわみ)と、
共役ばりの断面力(せん断力、曲げモーメント)を対応させて変換することで作ることができます。
つまり、実際のはりの変位y、たわみ角θに対して、
共役ばりでは曲げモーメントM、せん断力Sが対応しています。
したがって、実際のはりは、
固定端ではy=0、θ=0、
共役ばりでは、Mが0、Sが0になるのは、自由端となります。
また、実際のはりにおいては、自由端ではy≠0、θ≠0、
共役ばりでは固定端がM≠0、S≠0となります。
単純ばりの支点である可動支点、回転支点では、
y=0、θ≠0である。
共役ばりでM=0、S≠0となるのは、
実際のはりと同様に可動支点、回転支点となります。
片持ちばりでは、その固定端、自由端を入れ替えた片持ちばりに、
弾性荷重(M/EI)を載荷させなければならないことが理解できるでしょう。
このように弾性荷重(M/EI)を用いて、
はりのたわみ角、たわみを求める場合は、
共役ばりを用いなければなりません。
このモールの定理-共役ばり法は、
単純ばりの場合だけでなく、片持ちばりや張り出しばり、
不静定ばりにも応用できます。
ここで注意すべきことは、
共役ばりは、境界条件を満たすために仮想的に考えられたはりですから、
みかけ上、不安定なように見える場合もあります。
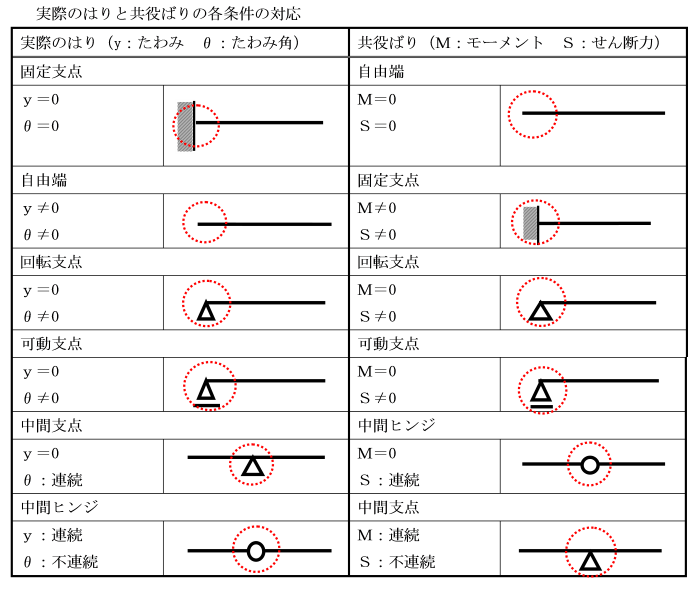
図の単純ばりのたわみ、たわみ角をモールの定理より求めなさい。
ただし、はり全体にわたり、曲げ剛性(EI)は一様とします。
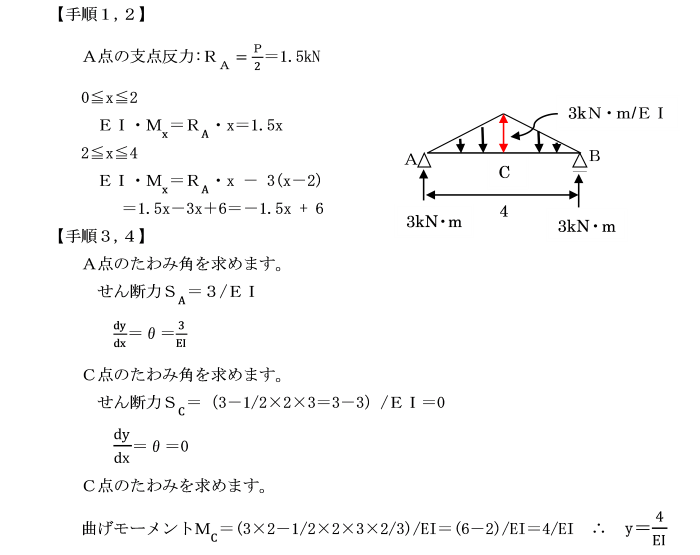
【手順1】 つり合い条件式より、反力、曲げモーメントMを求めます。
【手順2】 はりに弾性荷重(M/EI)を載荷します。
【手順3】 弾性荷重を載荷したはりの支点反力、断面力を求めます。
【手順4】 たわみ角:任意の点のせん断力。
たわみ :任意の点の曲げモーメント。
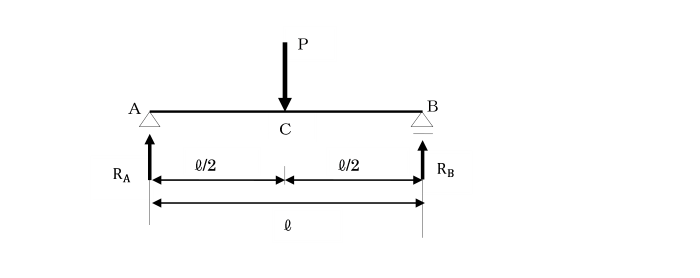
【例題1】
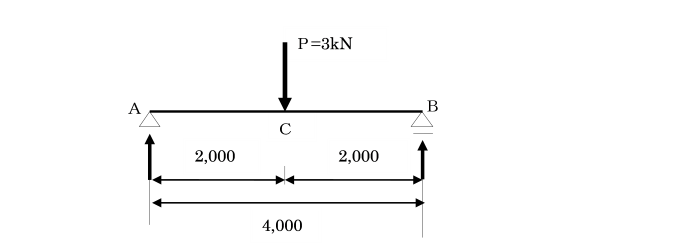
図のような単純ばりのたわみ角(支点A,B)、たわみ(C点)を計算せよ。
ただし、はり全体にわたり曲げ剛性(EI)は一様です。

【例題2】
図のような単純ばりのたわみ角(支点A,B)、たわみ(C点)を計算せよ。
ただし、はり全体にわたり曲げ剛性(EI)は一様です。


【例題3】
図のような単純ばりのたわみ角(支点A,B)、たわみ(C点)を計算せよ。
ただし、はり全体にわたり曲げ剛性(EI)は一様です。
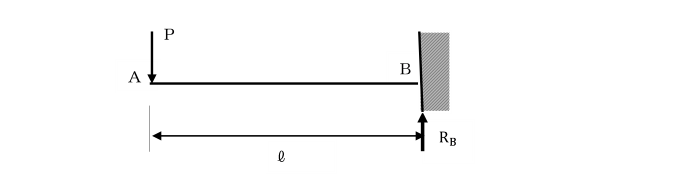

【例題4】
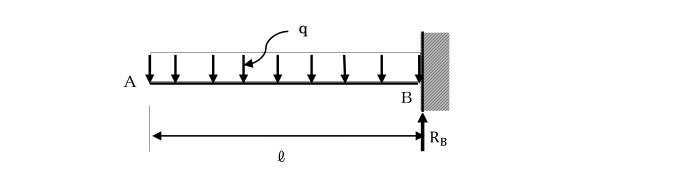
図のような片持ちばりのA点のたわみ角、たわみを計算せよ。
ただし、はり全体にわたり曲げ剛性(EI)は一様です。
【例題5】
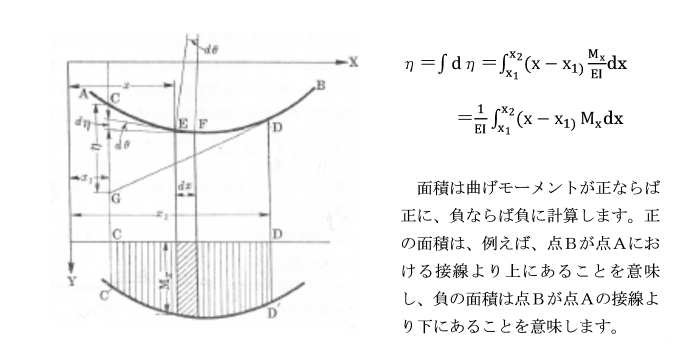
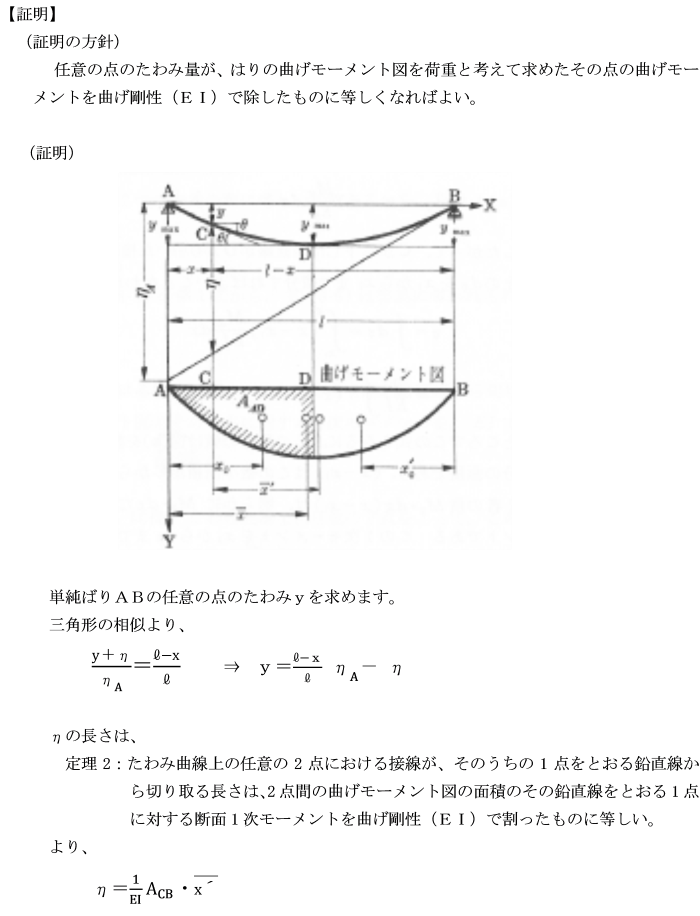
[第1定理] たわみ曲線上の任意の2点C´D´における接線の間の角θは、
これらの2点間の曲げモーメント図の面積を
曲げ剛性(EI)で割ったものに等しいことを証明せよ。


【例題6】
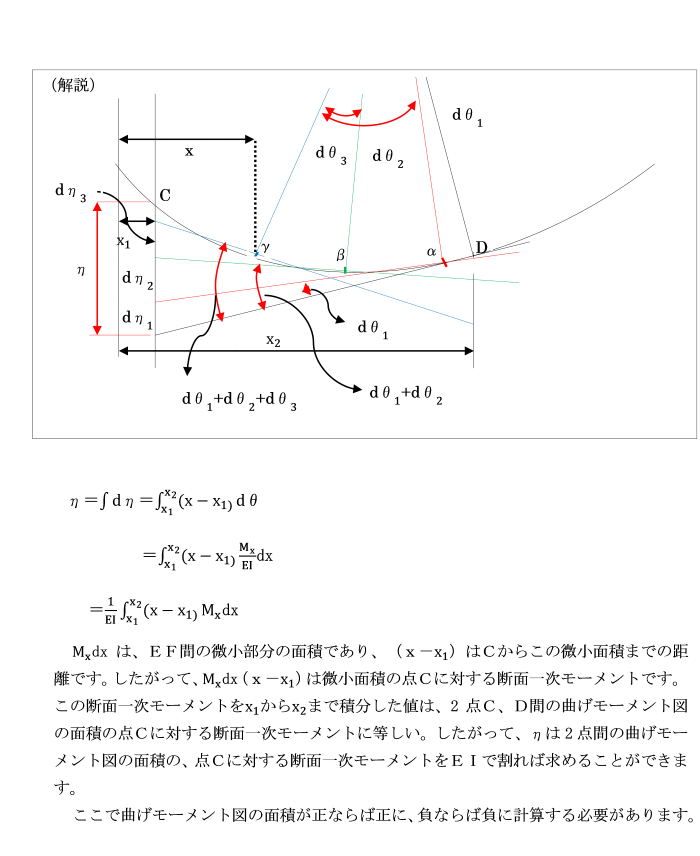
[第2定理] たわみ曲線上の任意の2点における接線が、
そのうちの1点をとおる鉛直線から切り取る長さηは、
2点間の曲げモーメント図の面積のその鉛直線をとおる1点に対する断面1次モーメントを
曲げ剛性(EI)で割ったものに等しいことを証明せよ。

【例題7】
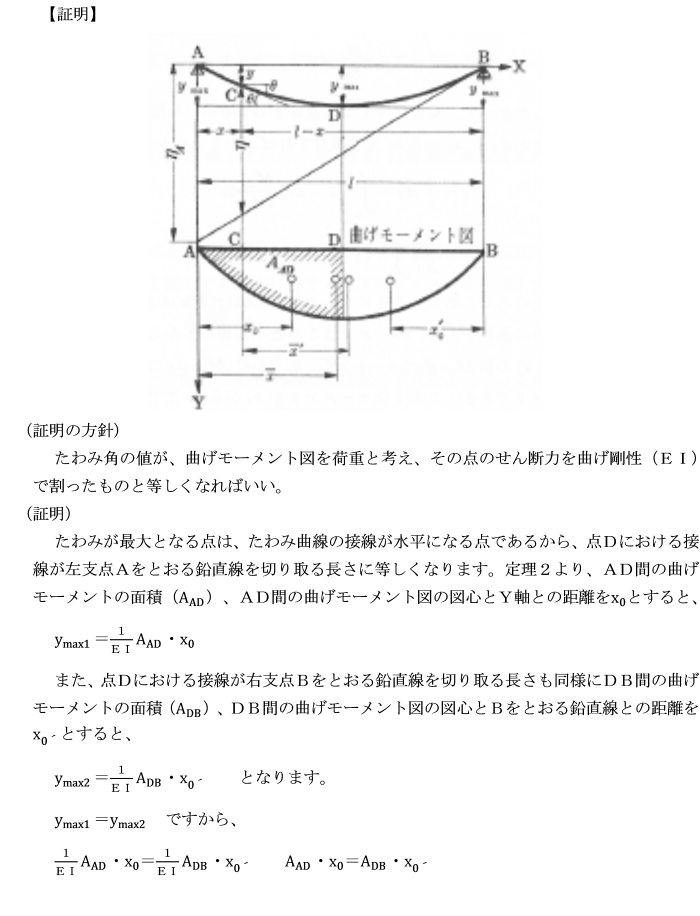
[第3定理] 単純ばりの任意点におけるたわみ角は、
曲げモーメント図を荷重と考えたときの、
その点に生ずるせん断力を曲げ剛性(EI)で割ったものに等しいことを証明せよ。

【例題8】
[第4定理] 単純ばりの任意点におけるたわみは、
曲げモーメント図を荷重と考えたときの、
その点に生ずる曲げモーメントを曲げ剛性(EI)で割ったものに等しいことを証明せよ。

続いてモールの定理を不静定ばりにも適用してみましょう。
次の手順により支点反力、断面力を求めます。
【手順1】 不静定力を設定し、静定基本系に分解します。
【手順2】 各々の静定基本系の曲げモーメント図Mを描きます。(弾性荷重M/EI)
【手順3】 不静定ばりを分解した静定基本系の共役ばりを設定します。
【手順4】 共役ばりに弾性荷重を載荷します。
【手順5】 実際の不静定ばりの境界条件を満足する量を求めます。
・実際のはりのたわみ:共役ばりの曲げモーメント
・実際のはりのたわみ角:共役ばりのせん断力
【手順6】 境界条件を満足するように
静定基本系に重ね合わせの原理を適用し、
変形の適合条件より方程式をつくり、不静定力を求めます。
・たわみが0 :曲げモーメントの重ね合わせが0
・たわみ角が0:せん断力の重ね合わせが0 等
【手順7】 不静定力が求まれば、
再度、実際のはりの曲げモーメント図M(弾性荷重M/EI)を描き、
共役ばりに載荷します。
【手順8】 任意の点のたわみ(曲げモーメント)、たわみ角(せん断力)を求めます。
【Ⅲ】 モールの定理により、枕片持ちばりの支点反力及び断面力を求めよ。
[枕片持ちばり:再掲]

[解法の手順]
【手順1】
不静定力を設定し、静定基本系に分解します。
RAを不静定力に選びます。
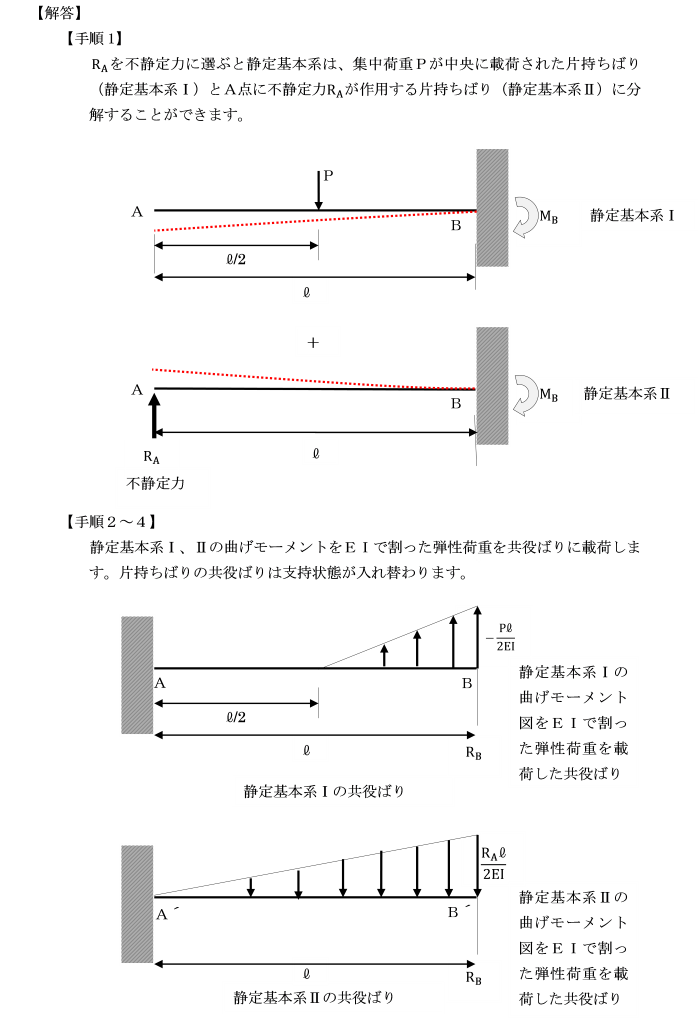
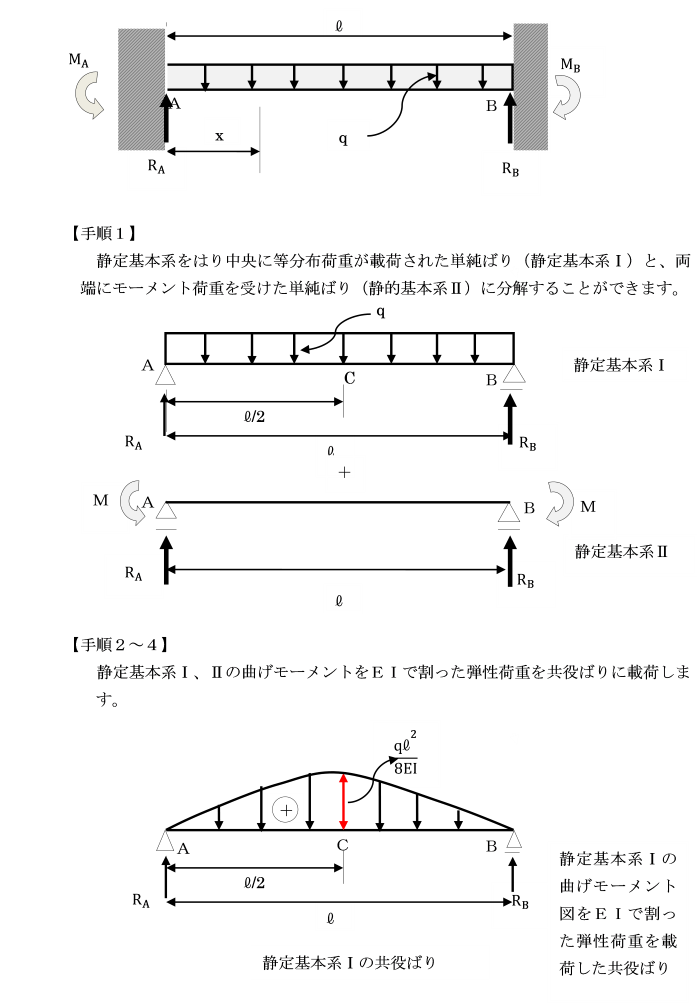
すると静定基本系は、等分布荷重が載荷された片持ちばり(静定基本系Ⅰ)と
A点に不静定力RAが作用する片持ちばり(静定基本系Ⅱ)に分解することができます。
【手順2】
各々の静定基本系の曲げモーメント図Mを描き、
分解した静定基本系の共役ばりを設定します。
静定基本系Ⅰ,Ⅱの曲げモーメントをEIで割った弾性荷重を共役ばりに載荷します。
【手順3】
実際の不静定ばりの境界条件を満足するように、
静定基本系に重ね合わせの原理を適用します。
変形の適合条件が満足する方程式をつくり、不静定力を求めます。
実際のたわみが0 → 共役ばりの曲げモーメントの重ね合わせが0
実際のたわみ角が0 → 共役ばりのせん断力の重ね合わせが0
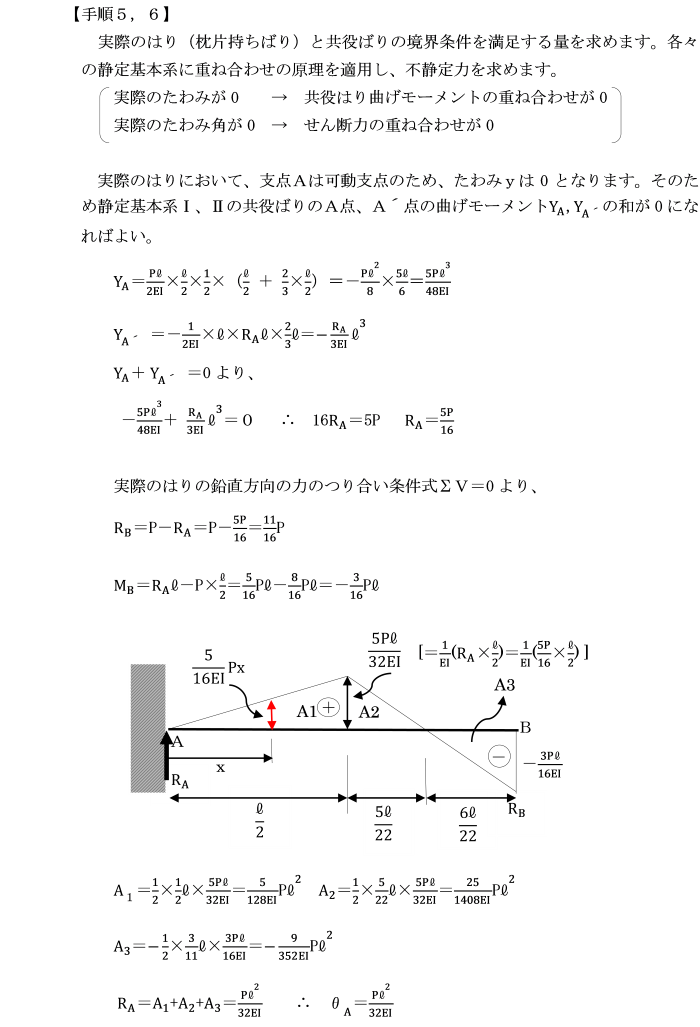
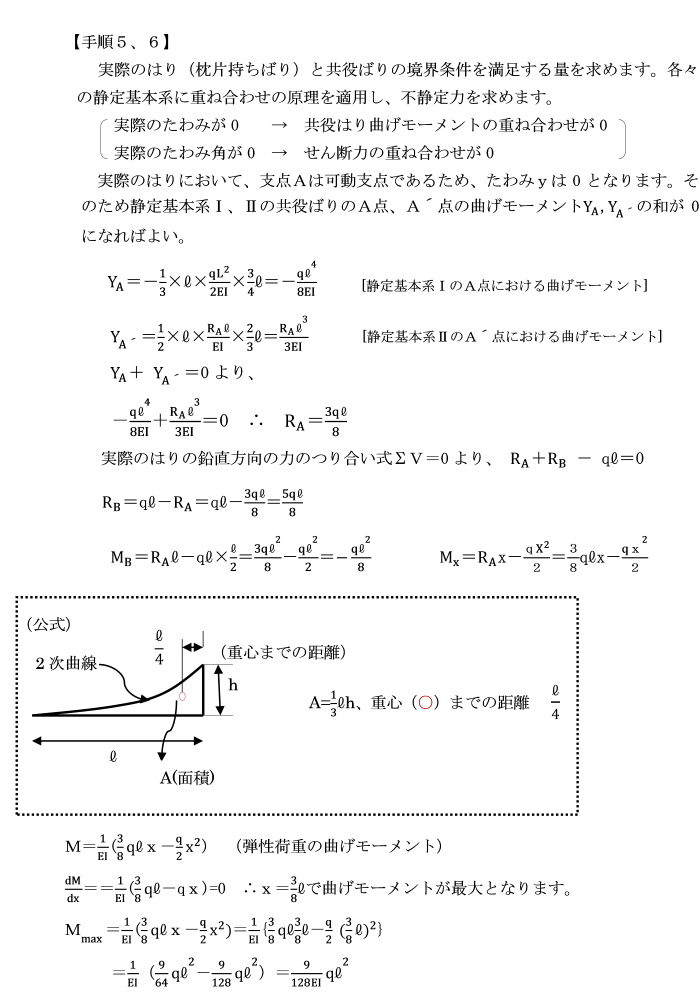
実際のはりは、支点Aが可動支点であるため、たわみyは0となります。
そのため静定基本系Ⅰ、Ⅱの共役ばりのA点、A´点の曲げモーメントYA,YA´ の和が0になればいい。
[静定基本系ⅠのA点における曲げモーメント]
YA=-1/3×l×ql2/2EI×3l/4=-ql4/8EI
[静定基本系ⅡのA´点における曲げモーメント]
YA´=1/2×RA l/EI×2l/3=RA l3/3EI
YA+ YA´=0より、
-ql4/8EI+RA l3/3EI=0 ∴ RA=3ql/8
実際のはりの鉛直方向の力のつり合い式ΣV=0より、
RA+RB -ql=0
RB=ql-RA=ql-3ql/8=5ql/8
MB=RAl-ql×1/2=3ql2/8-ql2/2=-ql2/8
Mx=RA・x-qx2/2=3qlx/8-qx2/2
M=1/EI(3qlx/8-q/2・x2) (弾性荷重の曲げモーメント)
dM/dx==1/EI(3ql/8-qx)=0 ∴x=3l/8で曲げモーメントが最大となります。
Mmax=1/EI(3qlx/8-qx2)/2 =1/EI{3ql/8・3l/8-q/2・(3l/8)2}
=1/EI(9ql2/64 -9ql2/128) =9ql2/128EI
【手順4】
不静定力が求まれば、
再度、実際のはりの曲げモーメント図M[弾性荷重(M/EI)]を描き、共役ばりに載荷する。
任意の点のたわみ(曲げモーメント)、たわみ角(せん断力)を求めます。
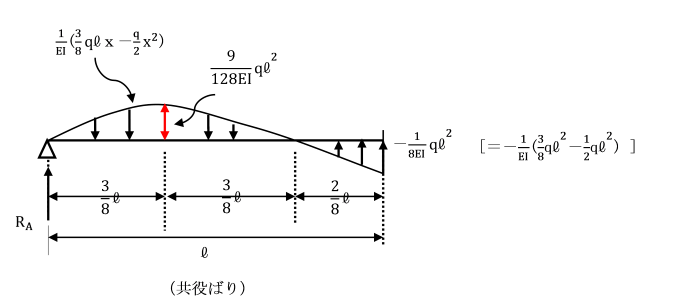
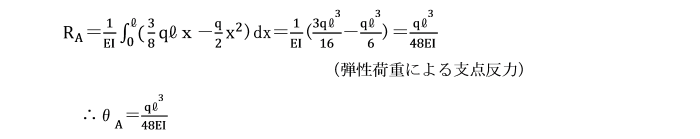
モールの定理において、任意の位置でのたわみ角の一般式θは、
任意断面xのせん断力を求めることにより得られることから、
次に、たわみyの一般式を求めます。

モールの定理より、任意点のたわみは、
曲げモーメント図を荷重と考えたときの、
その点に生ずる曲げモーメントを曲げ剛性(EI)で割ったものに等しい。
今、任意の位置としてa-a断面を考えます。
曲げモーメントMxは、支点Aからの距離であるため、
a-a断面での曲げモーメントを算定するためには、
微小部分の曲げモーメントの面積Mxdxにa-a断面からの距離X-xを乗じる必要があります。
これは、a-a断面を軸とする断面一次モーメントGxに相当します。
したがって、a-a断面での曲げモーメントは次のように表せます。
となります。
したがって、はり中央点のたわみycは、
8.4.4 とう性法
構造物の不静定次数を求め、
それと同数の過剰な反力を取り除いた後に残る構造物は、
静定基本系と呼ばれ、静定構造物に置き換えられます。
取り除いた部分に単位(=1)の不静定力を加え、
静定基本系の変位(たわみ)を求めます。
このときの変位をとう性という。
とう性と実際の荷重による静定基本系の変位を求めれば、
構造上の適合条件により、
「重ね合わせの原理」を用いて不静定力を求められます。
とう性法は、重ね合わせの原理を適用することから、
線形弾性的に挙動する構造物に用いられます。
【Ⅳ】とう性法により、枕片持ちばりの支点反力、断面力を求めよ。
[枕片持ちばり:再掲]

[解法の手順]
【手順1】
構造物の不静定次数を求めます。
n=m+r+p-2k
n:不静定次数
m:部材数
r:反力数(可動支点=1 回転支点=2 固定支点=3)
p:剛節接合材数(部材が持つ剛接に接合している材の数)
剛節接合材数p とは、ある部材に着目したときに、
その部材に剛に接合されている部材の数を表しています。
それぞれの節点に接合している部材の数字の最大値がその節点の剛節接合材数p
k:節点数(支点、自由端も1つの節点と数えます)
n=m+r+p-2k=1+4+0-2×2=1
∴ 1次の不静定構造物
【手順2】
不静定次数と同数の不静定力(支点反力あるいは断面力)を選択します。
ここでは支点反力RAを不静定力Xとして選択します。
【手順3】
不静定力を除いた後に残る静定基本系を設定します。
不静定力RAを除いた構造物を設定します。
その結果、基本構造は片持ちばりとなります。
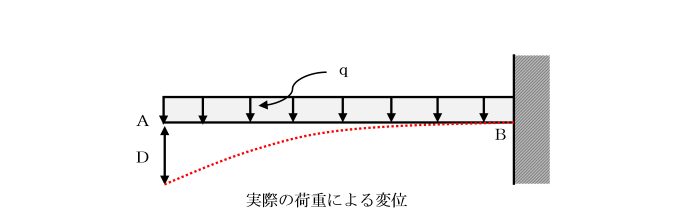
Dは、実際の等分布荷重qによって引き起こされる変位を示しています。
一般に変位の正の方向は、不静定力の正の方向とします。
【手順4】
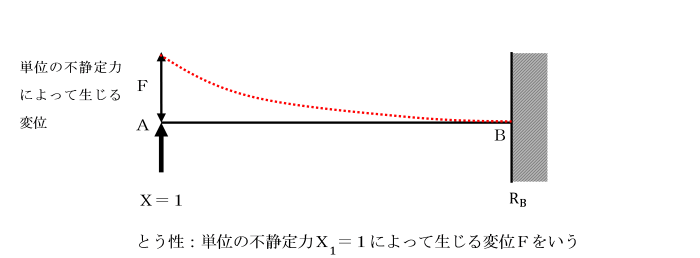
不静定力として単位(=1)の荷重を加えます。
[この単位の荷重に対応する基本構造の変位(たわみ)をとう(撓)性という。]
点Aに単位の不静定力X1=1を与えることにより生じる変位をFとします。
不静定力X1は、下から上に作用させているため、手順3の変位Dは、負の方向となります。
【手順5】
とう性と実際の荷重による変位が求まれば、
適合条件と重ね合わせの原理を用いて不静定力を求めます。
とう性Fは、単位の不静定力X1=1による変位であり、
また、Dは実際の荷重による変位です。
とう性F及び変位Dは、
一般的なたわみ公式から容易に求めることができます。
これら2つの変位を重ね合わせたものが、
全変位(たわみ)であり、点Aの境界条件(回転支点)より0となります。
つまり、実際の変位を生じさせるためには、
単位の不静定力によって生じる変位の何倍かが分かれば、
A点の支点反力を求めることができます。
したがって、次の適合方程式が得られます。
-D+FX=0
X以外の項は、すべて既知量であるから、
Xに関する一次方程式として解くことができます。
実際の荷重による変位Dを右辺に移行すれば、
FX=D
となり、とう性は不静定力Xの係数となります。
右辺は、はりに作用する荷重状態により変化します。
片持ちばりのたわみ公式より、
D=ql4/8EI (片持ちばりに等分布荷重qが載荷された場合の点Aのたわみ)
F=l3/3EI (はりの点Aに単位荷重P=1が載荷された場合の点Aのたわみ)となり、
l3x/3EI=ql4/8EI X=3ql/8
したがって、枕片持ちばりのA点での反力RAは、正の方向に3ql/8となります。
余剰の反力RAが求められれば、
残りの反力と全ての断面力は、静力学の平衡方程式から求めることができます。
つり合い条件式より、
ΣV=0より、 RA+RB=ql ⇒ 3ql/8+RB=ql ∴RB= 5ql/8
曲げモーメントの一般式Mは、x
Mx=RAx-qx2/2=3qlx/8-qx2/2 となります。
8.4.5 カスティリアノの第2定理(最小仕事の原理)
カスティリアノの第1定理を理解するために、
外力による仕事と内力による仕事について考えました。
構造物に外力が作用すれば、
外力の作用点は変位しますから、外力は仕事をします。
これを、外力による仕事といいます。
一方、外力が作用すると、
変位に起因して部材内部には変形が生じ、
同時に構造物内部には応力が生じます。
構造物内部で応力が変形に対して行う仕事を、
内力による仕事という。
内力による仕事は、
ひずみエネルギーとして構造物内に蓄積されます。
ひずみエネルギーは、仕事をする潜在的な能力を持っているため、
ポテンシャルエネルギーとも呼ばれます。
次に別種の仕事、いわゆる補助仕事W※について考えましょう。
これは、カスティリアノの第2定理を導く際に必要となり、
次式で定義されます。
補助仕事は、荷重-変位図の縦軸との間の面積で表されます。
これは、仕事Wのように物理的な意味は持っていません。
W+W※=P1δ1 の関係にあります。
補助エネルギーU※は補助仕事W※に等しい。したがって、
Pとδは力とそれに対応する変位です。
その結果、U※は、荷重Pの関数となります。
もし、複数の荷重(P1,P2,…,Pi,…Pn)が作用しており、
その内の1個の荷重Piに小さな増加荷重dPiが作用すれば、
補助エネルギーはdU※だけ増加します。すなわち、
dU※=(∂U※/∂Pi)・dPi
だけ増加します。この式は、補助エネルギーU※の増加dU※は、
Piに対するU※の変化割合とPiの増加dPiとの積に等しいことを意味しています。
この補助仕事は構造物の補助エネルギーU※の増加 dU※と同じものです。
補助仕事を行うのは、Piのみですから、
dU※=δidPi と表されます。
したがって、 ∂U/∂Pi・dPi=δidPi となり、
δi=∂U※/∂Pi という関係を得ます。
この式は、任意の荷重Piに関する補助エネルギーの偏微分係数は、
対応する変位δiに等しいことを表しています。
この式をクロッティ・エンゲッサの定理といいます。
この式は非線形構造物にも適用できます。
ここで、線形構造物であれば荷重と変位が比例します。
補助エネルギーU※とひずみエネルギーUは等しいことを利用し、
U※をUに置き換えますと、
δi=∂U/∂Piを得ます。
この式はカスティリアノの第2定理と呼んでいます。
つまり、線形構造物に対しては、
任意荷重Piに関するひずみエネルギーの偏微分係数は、対応する変位δiに等しい。
[最少仕事の原理(最小ポテンシャルエネルギーの原理)]
ポテンシャルエネルギーは、
その構造物が荷重を受けている状態から
受けていない状態に移行するときになされる仕事、
いわゆる潜在的なエネルギーとして定義されます。
構造物に作用している力には外力があり、
外力に起因して構造物内部に内力が生じます。
内力(断面力)のポテンシャルエネルギーUは、
構造物の中に蓄えられているひずみエネルギーです。
一方、外力のポテンシャルエネルギーは、
荷重を受けている状態から
受けていない状態に戻る際の負の仕事を意味します。
つまり、外力によるポテンシャルエネルギーは、

ここでPiは構造物に作用している荷重であり、
δiはそれに対応する変位を表し、
nは作用している荷重の個数です。
注意すべきは、外力によるポテンシャルエネルギーは、
外部仕事ではないということです。
つまり、外部仕事は、荷重Piの大きさが0から最終値まで徐々に増加し、
この荷重によってなされる仕事であるため、
Piδi/2となります。
外力によるポテンシャルエネルギーは、
構造物が最終の荷重を受けている状態から
受けていない状態に戻るときになされる仕事ですから
外部仕事とは異なります。
すなわち、構造物の全ポテンシャルエネルギーPEは、
内力によるひずみエネルギーUと
外力(荷重)によるポテンシャルエネルギーの和として得られます。
構造物の未知の節点変位D1,D2,…,Dnと
すべての荷重P1,P2,…,Pnが対応するものとすると、
今、全ポテンシャルエネルギーPEを
未知の節点変位Diについて偏微分すると、
∂PE/∂Di =∂U/∂Di -Pi となります。
カスティリアノの第1定理から、Pi=∂U/∂Di ですから、
∂PE/∂Di =∂U/∂Di-Pi=Pi-Pi=0 となります。
すなわち、未知の節点変位D1,D2,…,Dn全てについて適用できるので、
n個の連立方程式が得られます。
∂PE/(∂D1 )=0 ∂PE/∂D2=0 …… ∂PE/∂Dn=0
この原理は、弾性構造物(線形的あるいは非線形的)において、
全ポテンシャルエネルギーが、
未知の節点変位の関数で表されるならば、
任意の変位に関する偏微分係数が0をとるとき、
構造物はつり合い状態にあることを意味しています。
カスティリアノの第2定理δi=∂U/∂Pi より、
任意荷重Piに関するひずみエネルギーの偏微分係数は、
対応する変位δiに等しい。
不静定構造物が、不静定力の作用点で拘束されているためには、
変位が0にならなければならない。
したがって、∂U/∂Pi=0となります。
これは、ひずみエネルギーが最小の値をとることを意味しています。
最小仕事の原理は、カスティリアノの第2定理の特別な場合といえます。
このことは、構造物に荷重が作用している場合、
荷重と不静定力との力系が、
構造物のひずみエネルギーUを最小に保つように作用することを意味しています。
∂U/∂Pi=0 を最小仕事の原理といい、
不静定構造物の不静定力(支点反力)を求めるのに適用されます。
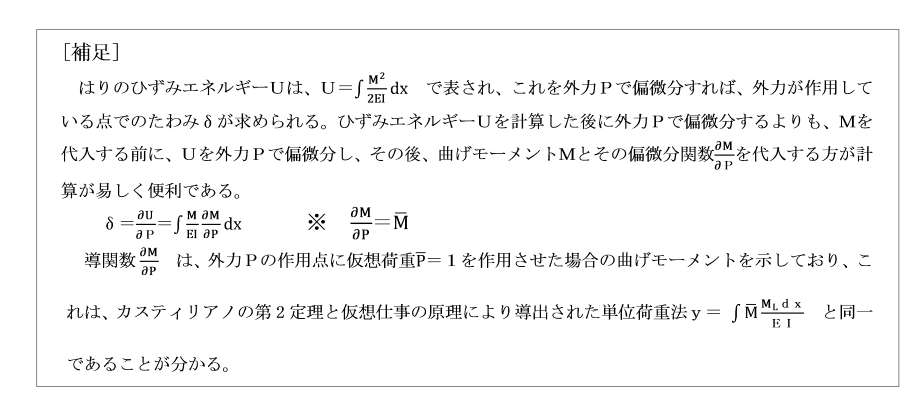
【Ⅴ】カスティリアノの第2定理により、枕片持ちばりの支点反力、断面力を求めよ。
[枕片持ちばり:再掲]

[解法の手順]
【手順1】
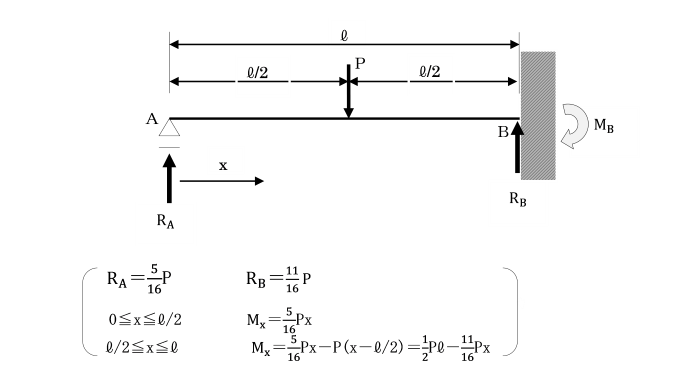
支点Aを取り去り、点Bを固定端とする片持ちばりを考えます。
【手順2】
点Aに不静定反力RAを外力として作用させます。
図(a)と図(b)を重ね合わせた荷重の載荷状態を考えます。
すると元の枕片持ちばりと等価な力学系となります。
図(a)の点Aからの距離をxとすれば、
任意の断面xにおける曲げモーメントM(a)は、
M(a)=-qx2/2
図(b)の任意の断面xにおける曲げモーメントM(b)は、
M(b)=RA・x となります。
枕片持ちばりの任意断面における曲げモーメントMxは、重ね合わせの原理より、
Mx=M(a)+M(b)=-qx2/2+RA・x となります。
【手順3】
はりの変形は、曲げモーメントが卓越しているから、せん断力の影響を無視してひずみエネルギーUを計算します。
ひずみエネルギーUは、
と表され、カスティリアノの第2定理 δi=∂U/∂Pi を適用します。
点AのたわみδAは、
で表されます。
Mx=M(a)+M(b)=-qx2/2+RA・x ⇒ ∂Mx/∂RA=x
実際、点Aは回転支点で拘束されますから、たわみは0です。
δA=[-ql4/8+1/3・RAl3]=0 ⇒ 1/3・RAl3=ql4/8 ∴ RA=3ql/8
RA+RB=ql より、RB=5ql/8
MB=3ql2/3-ql×l/2=-ql2/8
曲げモーメントの一般式Mxは、Mx=RAx-qX2/2=3qlx/8-qx2/2 となります。
次に、はり中央点のたわみを
カスティリアノの第2定理(最小仕事の原理)により求めよ。
本例は、等分布荷重qが載荷されています。
このはりの任意の点のたわみを求める場合、
与えられた荷重のほかに、更にたわみを求めたい点に仮想集中荷重Pを載荷し、
ひずみエネルギーUを計算します。
計算されたUを外力Pで偏微分した後、P=0とおけば、
その点のたわみを求めることができます。すなわち、
y=(∂U/∂P)P=0
ここでは、反力等は求められているものとします。
8.4.6 三連モーメントの定理
三連モーメントの定理は、
モーメントを未知数にとった不静定ばりの解法で、応力法の一つです。
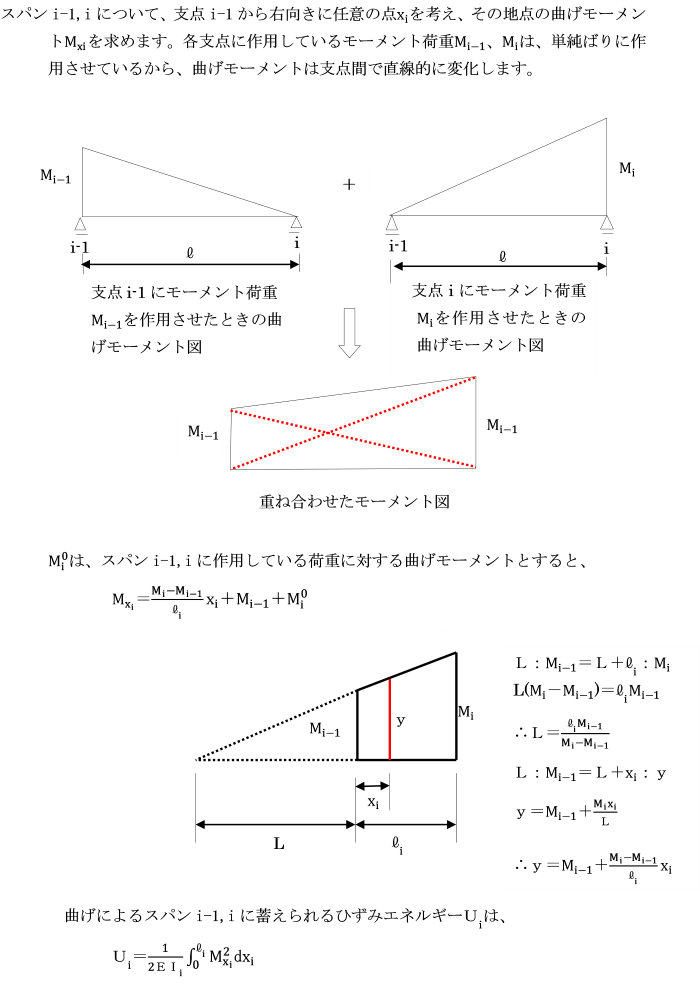
互いに隣り合う三つの支点に働く曲げモーメントMn-1,Mn,Mn+1を関連づけることから
三連モーメントと呼ばれます。
モールの定理より、部材ABを単純ばりと考え、
これに曲げモーメントMxの1/EIを分布荷重(弾性荷重)として作用させると、
点Aのせん断力(支点反力)は、
支点Aの接線回転角τAになります。
同様に、点Bのせん断力(支点反力)は、
支点Bの接線回転角τBに負号をつけたものになります。
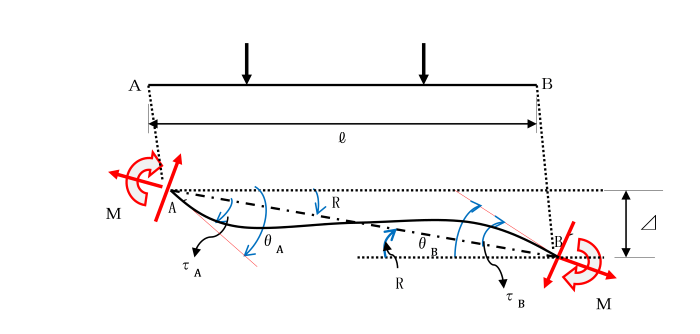
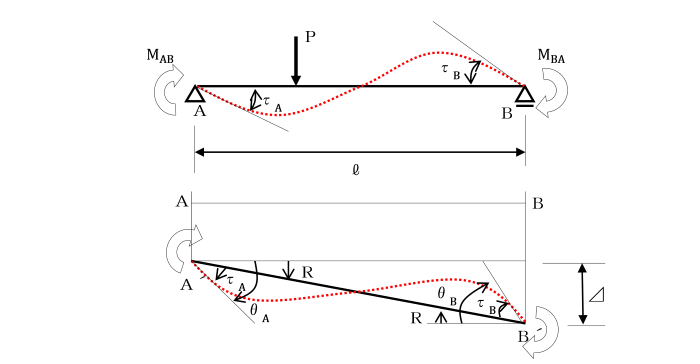
[三連モーメントの定理の誘導1]
変形後の部材A´B´は、変形前の部材ABに対して角Rだけ回転しています。
部材ABの相対変位を⊿、部材長さをlとすると、
R=⊿/lを部材回転角という。
次に変形後の節点A´,B´から部材のたわみ曲線に引いた接線と
線分A´B´のなす角τA、τBをそれぞれ接線回転角といいます。
また、これらの接線が変形前の部材軸線ABとのなす角θA、θBを
節点回転角あるいは、たわみ角といいます。
たわみ角θと接線回転角τ、部材回転角Rとの間には、
θA=τA+R θB=τB+R という関係があります。
モールの定理より、任意断面のたわみ角は、
弾性荷重(M/EI)を作用させたときの、その断面におけるせん断力に相当するから、

部材ABを単純ばりと考え、
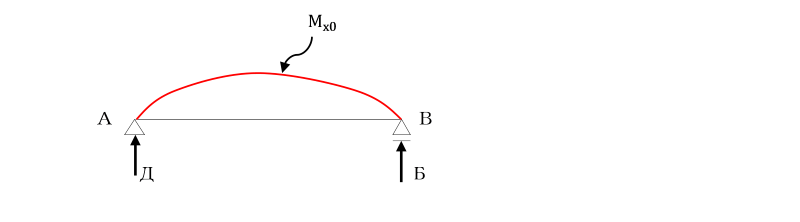
外力としてはり両端にモーメント荷重MA、MBが作用しています。
任意断面における曲げモーメントをそれぞれMxA、MxBとします。
また、単純ばりAB間に、
任意の荷重が作用した場合の曲げモーメントをMx0とする。
曲げモーメントの一般式Mxは、重ね合わせの原理より、
Mx=Mx0+MxA+MxB
=Mx0+MA(l-x)/l+MBx/l
となるので、
Д及びБは、ABを単純ばりと考え、
はりAB間に作用する荷重による曲げモーメントMx0を荷重とした場合の
A点及びB点における支点反力です。
たわみ角θ、接線回転角τ及び部材回転角Rとの間には、
θA=τA+R、θB=τB+R の関係から、
θA=1/EI[l/6(2MA+MB)+Д]+R
θB=-1/EI[l/6(MA+2MB)+Б]+R になります。
今、任意の2つの部材AB、BCを考え、
その長さ、断面2次モーメント及び部材回転角をlAB,lBC,IAB,IBC,RAB,RBCとします。
もし、断面2次モーメントI、スパンlとも全スパンにわたり同一の時には、次のようになります。
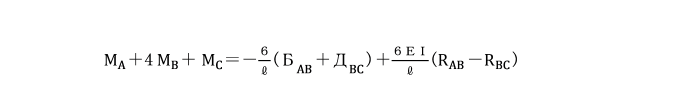
この式におけるБ、Дは荷重条件より求められます。
これらを三連モーメントの定理の荷重項と呼びます。
荷重項の値は、ABを単純ばりと考え、
はりに作用する荷重による曲げモーメントMx0を荷重とした場合のA点及びB点における支点反力、
つまり、モールの定理における両支点のたわみ角の絶対値をEI倍したものです。
[三連モーメントの定理の誘導2]
一つの直線部材を3つ以上の支点で支持し、
その一つの支点は回転支点、他の支点は、
可動支点であるような2スパン以上の直線ばりを連続ばりという。
はりは連続しているため、
中間支点においても曲げモーメントを生じ、
たわみ曲線は波形になります。
連続ばりを解くには、
はりの両端に支点を持つ単純ばりを静定基本系とし、
中間支点の反力を不静定力として取り扱う解法が考えられます。
今、各々の中間支点を仮想切断し、
曲げモーメントの伝達を断った構造を考えると、
これは単純ばりが連続したものとなります。
各々のスパンが単純ばりであるため、
スパンごとに独立したたわみが生じ、
たわみ曲線は支点上で、折れ線をなします。
そこで、各々の中間支点上の仮想切断面に
向きが反対で同じ大きさのモーメント荷重を加えて、
左右両スパンのたわみ曲線が、
連続ばりのたわみ曲線と一致するようにすれば、
各々の単純ばりは、
元の連続ばりの状態になります。
三連モーメントの定理は、
反力を不静定力とするのではなく、
曲げモーメントとする解法です。
支点上の左右のたわみ角が
等しいことを利用して三連モーメントの式を誘導することができます。
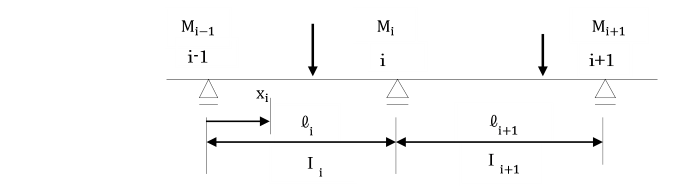
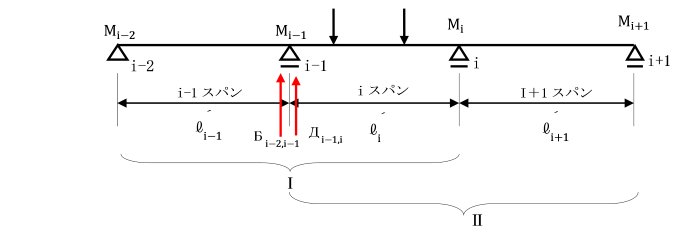
今、連続ばりの任意の隣接2スパン(支点をi-1,i,i+1)を考え、
両スパンについて支点iのたわみ角θi,i-1
及びθi,i+1をカスティリアノの第2定理を用いて求めます。
各スパン長、断面2次モーメントは、
それぞれli,li+1及びIi,Ii+1とし、
各支点における曲げモーメントを
Mi-1,Mi,Mi+1とします。
支点沈下は考慮しないものとします。
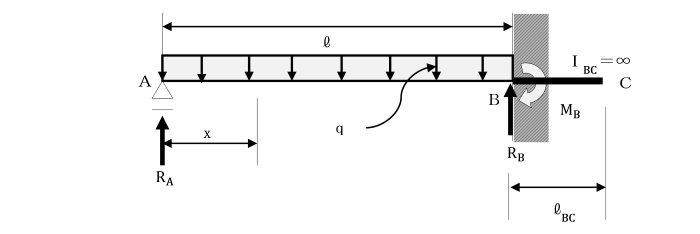
【Ⅵ】三連モーメントの定理により、枕片持ちばりの支点反力、断面力を求めよ。
[枕片持ちばり:再掲]

[解法の手順]
【手順1】
点Bは固定端ですので、点Bの右側にIBC=∞のはりlBCがあるものとして、
三連モーメントの定理を適用します。
【手順2】
【手順3】
境界条件を導入します。
点Aは可動支点ですので、曲げモーメントMA=0 となります。
EAB=ql3/24 (三連モーメントの荷重項より)
БABは、単純ばりABに作用する荷重による曲げモーメントMを荷重とした場合の、B点の支点反力です。
l/I・MA+2(l/I)MB=-6(БAB/I) に代入すると、
MB=-ql2/8 となります。
点Bをモーメントの中心とすると、
ΣMB=RAl-ql×l/2+ql2/8=0
RAl=3ql2/8 ∴ RA=3ql/8
また、RA+RB=ql より、RB=5ql/8
したがって、曲げモーメントの一般式Mxは、
Mx=RAx-qX2/2=3qlx/8-qx2/2 となります。
8.4.7 定点法
(1)定点
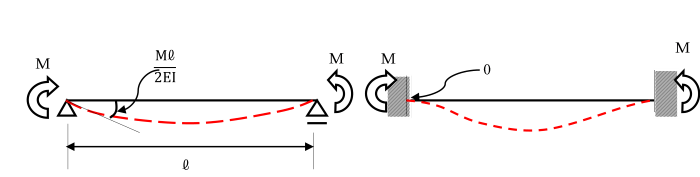
単純ばりの両端にモーメント荷重Mを作用させた場合の回転角は、
Ml/2EIとなります。
また、両端固定のはりの両端にモーメント荷重Mが作用した場合の回転角は0となります。
このように、はりの結合状態により回転角は異なります。
例えば、曲がりやすいはりABと、
曲がりにくいはりA´B´がそれぞれ同じ剛度の柱CDに結合されています。
曲がりやすいはりABは、
ほとんど固定端に結合したような変形(回転角が0)をします。
曲がりにくいはりA´B´は、
ヒンジ支点のように変形します。
つまり、はりの結合状態は、結合される側の剛度だけでなく、
結合する側の剛度との相関関係によることが分かります。
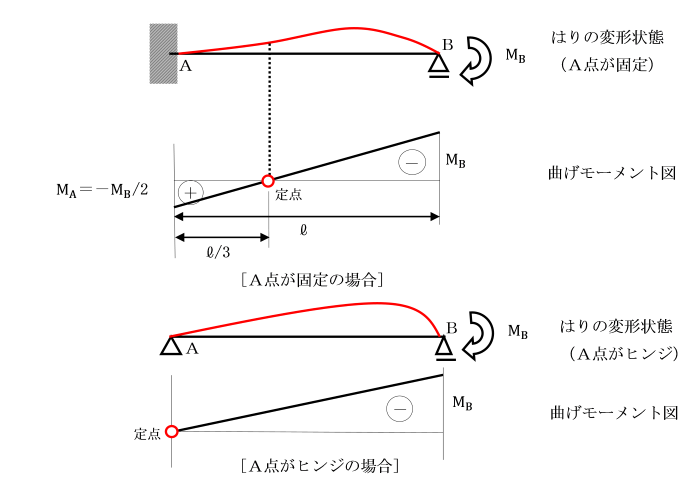
今、A端が完全に固定され、B端が可動支点のはりを考えます。
B端にモーメント荷重MBを作用させます。
するとはりの曲げモーメント図は、図のようになります。
この場合、曲げモーメントが0になる地点は、
A端より1/3の距離です。
この点は、MBの大きさには関係なく決まった点となります。
このような曲げモーメントが0になる点を定点といいます。
A点がヒンジの場合、定点はA端になります。
A端が弾性固定の場合、
定点はA端とl/3との間にあることが想定されます。
すなわち、定点がA端に近いときは、
固定の程度が低く、l/3に近いときは、完全固定に近いことを意味しています。
定点は、A点にモーメント荷重が作用する場合と、
B点に作用する場合を考えると、
一部材に2個存在します。
これらを区別するために、水平材、鉛直材でそれぞれ、左及び下に存在する定点をJ、
また、右及び上に存在するものをKで表します。
なお、定点から近い方の材端までの距離を定点距離といい、
J,Kに対して、それぞれa,bで表します。
(2)定点比
図のように支点iより右側にあるスパンに荷重が載荷されている連続ばりを考えます。
この連続ばりの支点iのすぐ右側断面で仮想的に切断して、
2つの部分に分けます。
この断面の右側部分が左側部分に及ぼす影響は、
支点iに作用する曲げモーメントMiと、
せん断力Siで置き換えることができます。
このMiは、左側部分の各スパンに曲げモーメントを伝達します。
一方、Siは、支点iによって支えられるので、
左側部分のスパンに何ら影響は与えません。
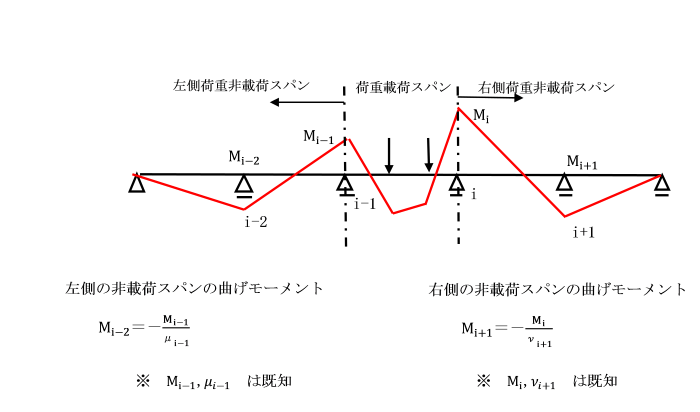
下図に示すように非載荷スパンがあります。
絶対値の大きい方の支点のモーメントを小さい方の支点のモーメントで割り、
負号をつけたものを定点比といいます。
定点は、各スパンに左右1個ずつあるから、
定点比も各スパンに2個存在します。
左定点比:μi=-Mi/Mi-1 右定点比:νi=-Mi-1/Mi
連続ばりの曲げモーメントを求めるとき、
荷重載荷スパン左側の非載荷スパンでの曲げモーメントは、
左定点比を用います。
また、荷重載荷スパン右側の非載荷スパンでの曲げモーメントは、
右定点比を用います。
(3)定点比の決定
[非載荷スパンの場合]
連続ばりから隣接する2つの非載荷スパンを取り出し、
三連モーメントの定理を適用します。
λi-1 Mi-2+2(λi-1+λi)Mi-1+λiMi=0 ここで λi=IC/Iili
同様にして、右定点比に対しては、
これらの式は、定点比を決定するための漸化式です。
左定点比μ1が分かれば、以後の定点比を求めることができます。
同様にして、右定点比ν4が分かれば、以後の定点比が順次確定します。
[荷重載荷スパンの場合]
次に図のような支点i-1,i間に荷重が載荷されている連続ばりを考えます。
ⅠのスパンとⅡのスパンに三連モーメントの定理を適用します。
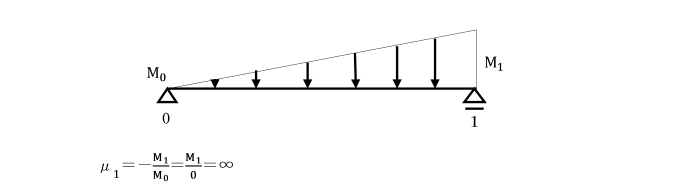
例えば、図のような支点0が回転支点の場合、左定点比μ1は、次のようになります。
また、支点0が固定支点の場合の左定点比μ1を求める場合は、
支点0の左側に微小なスパンl0、断面2次モーメントI0=∞を仮想的に追加して考えます。
この微小スパンの左定点比μ0を求めると、次のようになります。
【Ⅶ】 定点法により、枕片持ちばりの支点反力、断面力を求めよ。
[枕片持ちばり:再掲]

[解法の手順]
左定点比μ1は、支点Aがヒンジであるため、
μ1=-MB/MA=-MB/0=∞となります。
また、支点Bは固定端です。
B点の右側に仮想の微小なスパンlP、断面2次モーメントIP=∞を考えますと、
8.4.8 単位荷重法
単位荷重法は、仮想仕事の原理を用いて、
構造物の任意の変位(たわみ)を求める方法です。
仮想仕事は、仮想内力仕事の総和は、
仮想外力仕事の総和に等しいというエネルギーの保存の法則を利用します。つまり、
仮想荷重×実変位=仮想荷重による断面力×実変形
が成立することを利用しています。
理論的には静定構造物にも不静定構造物にも適用できますが、
構造物全体の断面力が求められていることが前提です。
単位荷重法の基礎方程式が、
仮想仕事の原理から導かれます。
そのためこの方法自身が仮想仕事の原理と呼ばれることもあります。
それでは、仮想仕事の原理についてみていきましょう。
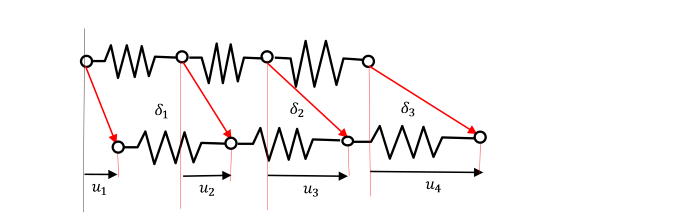
構造物の一部を取り出した次のような構造物を考えます。
この構造物は、4つのヒンジが3本のばねで結ばれています。
「変形の式」と「つり合いの式」は、独立して考えることができます。
今、次のような恒等式を考えます。
S1(u2-u1)+S2(u3-u2)+S3(u4-u3)=-S1u1+(S1-S2)u2+(S2-S3)u3+S3u4
この式の左辺の各項はS1, S2及びS3でまとめたものであり、
右辺はu1, u2,u3及びu4でまとめたものである。
この式は単なる恒等式で、両辺を分解して整理すれば、
「0=0」しか得られない。
この恒等式に、「変形の式」と「つり合いの式」を左辺と右辺にそれぞれ代入すると、
次のような関係式が得られます。
S1(u2-u1)+S2(u3-u2)+S3(u4-u3)=-S1u1+(S1-S2)u2+(S2-S3)u3+S3u4
S1 δ1 +S2δ2 +S3δ3 = F1u1+ F2u2+ F3u3+F4u4
これを仮想仕事の式といい、
あるいは仮想仕事の原理という。
ここで、「仕事」の由来は、
左辺が、ばねに生じている部材力(内力)と
全く別の系での外力の作用により生じた変位との積です。
一方、右辺は、4つの外力と全く別の系での各ばねに生じている変位との積です。
また、「仮想」の由来は、2つのモデル(変形の式、つり合いの式)が、
力学的に全く別のものです。
変形の系とつり合いの系との間には何ら関係がありません。
つまり、力が作用して変形が生じたという実際の仕事ではありません。
特に左辺の各項は仮想内力仕事、
右辺の各項は仮想外力仕事ということです。
したがって、仮想仕事の式は、
仮想内力仕事の総和は、
仮想外力仕事の総和に等しいことを示しています。
このようにして導かれた仮想仕事の式は、
力学的な方法で得られたものではなく、
数学の恒等式によるものです。
仮想変位は、構造物系に任意に課された想像上の変位であり、
構造物に作用した荷重によって引き起こされるたわみのような実際の変位ではありません。
仮想変位と実在の力による仕事を仮想仕事という。
[構造物への適用]
構造部材に外力が作用した場合、
部材は変位します。
また、外力に抵抗するため部材内部には変位に伴い変形が生じ、
同時に内力が生じています。
今、部材に仮想変位を与えると、
外力は仮想変位に対し外部仕事を行う。
また、外力によって生じた内力と仮想変位に起因して部材内部に変形(ひずみ)が生じ、
これら内力と変形(ひずみ)は内部仕事を行う。外部仕事と内部仕事は等しい。
Wext=Wint
Wext:外部仕事 Wint:内部仕事
構造物は外力の作用により変形を生じるので、
仮想仕事の原理を適用する際には、
① 外部仕事のほかに内部仕事を考慮する。
② 仮想変位は構造物の支持条件に適合する。
③ 構造物の連続性を保持する。
仮想変位は、構造物系に任意に課された想像上の変位であり、
実際の荷重によって生じた構造物の変位ではありません。このことは重要なことです。
外部仕事Wextは、仮想変位をする間に、
構造物に作用している荷重によってなされる仕事です。
構造物に作用している荷重は、
静的に作用している荷重ですが、
仮想変位が加えられる時点では既に、その最終の値で作用し続けています。
したがって、外力(荷重、反力)による仮想仕事は、単純に外力と変位の積で表されます。
内部仕事Wintは、仮想変位に起因し、
部材内部には軸方向変形、曲げ変形、せん断変形が生じます。
この仮想変形は、実際に外力によって生じた内力(軸方向力、曲げモーメント及びせん断力)に対応し、
仮想仕事がなされます。
ここで注意すべきは、
仮想変形は、実際に生じている内力によって引き起こされているものではありません。
また、軸方向力によって仮想仕事N×δ⊿がなされるが、
曲げモーメント、せん断力によっては全く仮想仕事はなされません。
つまり、曲げモーメントに対応する仮想変形は、曲げ変形δθであり、
その仮想仕事は、
M×δθ、
同様にせん断力によりδλが生じ、その仮想仕事は、S×δλとなります。
このようにして構造物の1つの要素に実際の荷重により生じる内力による内部仮想仕事は、
Nδ⊿+Mδθ+Sδλ となります。
構造物全ての要素について積分すれば、
Wint=∫Nδ⊿+∫Mδθ+∫Sδλ
が得られます。
この式の中で、N、M及びSは、
実際の外力によって構造物中に生ずる内力であるのに対し、
変形δ⊿、δθ及びδλは、
構造物の仮想変位に伴い生じる想像上の変形です。
単純ばりを例に仮想仕事の原理を整理してみましょう。
はりに荷重P1,P2,P3が載荷され、
それぞれdδ1 ,dδ2,dδ3のたわみが生じます。
今、任意の仮想変位をδ1,δ2,δ3を与えます。
外部仕事Wextは、仮想変位δ1,δ2,δ3に対して、
はりに作用している荷重P1,P2,P3によってなされる仕事であるから、
となる。
また、はりに荷重P1,P2,P3が作用すると、
部材内部に断面力として曲げモーメントM、せん断力S、軸方向力Nが生じます。
仮想変位δ1,δ2,δ3に起因し、
はりには仮想の曲げ変形δθ、せん断変形δS、軸方向変形δ⊿が生じます。
その結果、内力である曲げモーメントによってなされる仮想仕事Mδθ、せん断力S及び軸方向力Nにより、
それぞれSδS、Nδ⊿の仮想仕事がなされます。
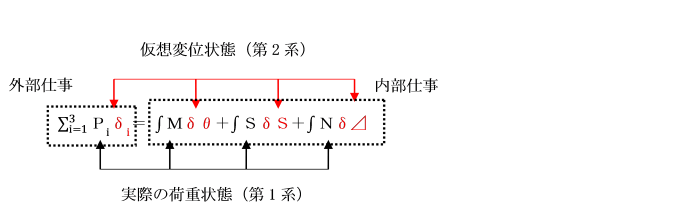
したがって、内部仕事Wintは、
Wint=∫Mδθ+∫SδS+∫Nδ⊿ となります。
Wext= Wintより、
この式の左辺は、仮想変位に対して外力がなす仮想仕事を表しており、
右辺は内力(部材力)がなす仮想仕事を表しています。
M、S、Nは、実際荷重Pi(この両者を第1系と称す)によって生じた内力です。
この両者は切り離せない関係にあります。
同時にδiとδθ、δS、δ⊿(この両者を第2系と称す)
すなわち、δθ、δS及びδ⊿は、δiに起因して生じた部材の変形です。
しかしながら第1系(実際荷重PiとM、S、Nの組)と
第2系(δiとδθ、δS及びδ⊿の組)との間には何らの関係も存在しない。
そこで、第1系として(実際荷重PiとM、S、Nの組)の代わりに仮想荷重(Pi )
ならびにそれによって引き起こされる断面力M 、S 、N 、をとります。
第2系としては、δiとδθ、δS及びδ⊿の代わりに、
実際荷重による変位及び変形量(dδiとdθ、dS及びd⊿)を用いても差し支えありません。
この式は、構造材料の特質や線形挙動を条件としておらず、
適用するにあたっては、重ね合わせの原理が成立する必要はありません。
しかし、構造材料が、フックの法則にしたがい、
構造物も線形的挙動する場合を考えます。
その際、構造物に作用する実際の荷重によって引き起こされる変形dθ、dλ、d⊿を求めると、
曲げ変形dθ=(ML dx)/EI、せん断変形dλ=(κSL dx)/GA、軸方向変形d⊿=(NLdx)/EA
※ML,SL,NL:実際の荷重によって生じる曲げモーメント、せん断力、軸方向力となります。
これらの関係を代入すると、
この方程式は、構造物の任意の点の変位を求めるのに用いられます。
曲げ変形dθ=MLdx/EI、せん断変形dλ=κSL dx/GA、軸方向変形d⊿=NLdx/EAの誘導
[単位荷重法の導出]
仮想仕事における外部仕事と内部仕事が等しいという関係を用いて、
実際の荷重における任意の点のたわみを求めます。
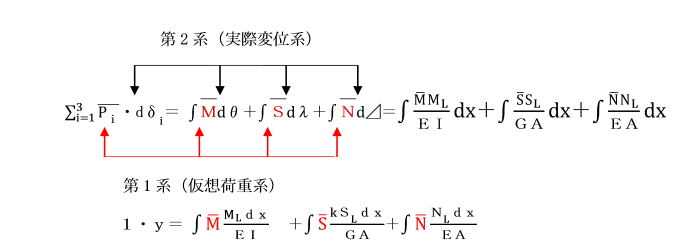
次の第1系は、仮想荷重Pi並びにそれによって引き起こされる断面力M(曲げモーメント),S(せん断力),N(軸方向力)をとり、第2系として実際荷重による変位及び変形量をとります。
この方程式においてyはたわみを求めたい点での変位で、
たわみ角であることもあります。
M,S,Nは、単位荷重による曲げモーメント、せん断力及び軸方向力で、
dθ,dλ,d⊿は、実際の荷重によって引き起こされた変形を表します。
この方程式は、構造材料がフックの法則にしたがい、
構造物も線形的に挙動する場合の式です。
例えば、トラス構造のようにピン継手の節点だけに荷重を受けるならば、
曲げ、せん断変形が生じず、軸方向変形だけが必要となります。
また、はりあるいはラーメン構造の場合は、
曲げ変形が卓越し、単位荷重法は単純化されて、
曲げ変形だけの式となります。
一般に、構造物の形式に応じて、式中各項の適当な組み合わせをとり、
構造物の変位を計算することができます。
【Ⅷ】単位荷重法により、枕片持ちばりの中央点のたわみycを求めよ。
[枕片持ちばり:再掲]

[解法]
はり構造は曲げ変形が卓越しているから、
曲げ変形のみを考えます。
中央点のたわみycの計算
【手順1,2】
求めるたわみの箇所に単位荷重P=1を載荷し、
曲げモーメントMを求めます。
8.5 変位法による解法
8.5.1 剛性法

剛性法では、未知量は構造物の節点変位です。
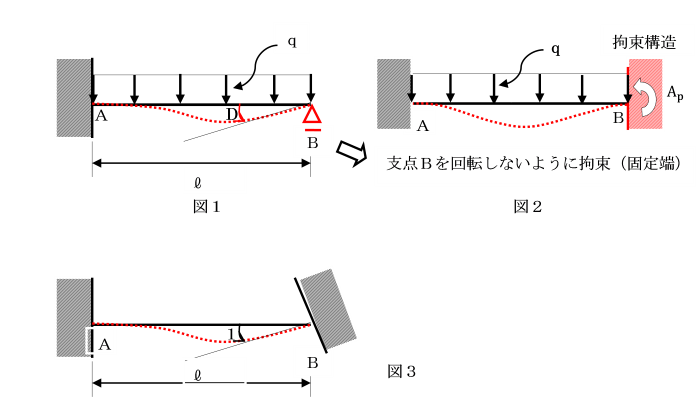
剛性法の概念を理解するために、図1のようなはりを考えます。
Aは固定端、Bは可動支点を持ち、
等分布荷重qが載荷されています。
未知節点変位は、支点Bにおける回転Dだけです。
ここで、未知節点変位Dが0になるように構造上の変更を加え、
節点が移動、回転しないように拘束(固定端)することによって、
回転を0にすることができます。
このようにして得られる構造を拘束構造(図2)という。
図1の拘束構造は、図2に示すような支点Bを回転しないように固定端とすることにより得られます。
拘束構造のはり(図2)に等分布荷重が載荷されれば、点Bには曲げモーメントが生じます。
この曲げモーメントは未知節点変位Dに対応する作用であり、
固定端構造により引き起こされます。
実際のはりは、点Bでは、
曲げモーメントが生じない代わりに回転角Dが生じます。
一方、拘束構造のはり(図2)は、
点Bで曲げモーメントが生じる代わりに
回転角Dが生じません。
つまり、図3のはりにおいて、
点Bに単位の回転角1を作用させ、
それのD倍の回転角を生じさせる部材剛性と、
図2の点Bの曲げモーメントの値が、
同じ効果であるという考え方を利用するものです。
図2の点Bの曲げモーメントをApとします。
この曲げモーメントは、Dに対応するものですから、
その方向も反時計回りを正(+)とします。
Apは、両端固定ばりに等分布荷重qが載荷された場合の点Bでの曲げモーメントですから、
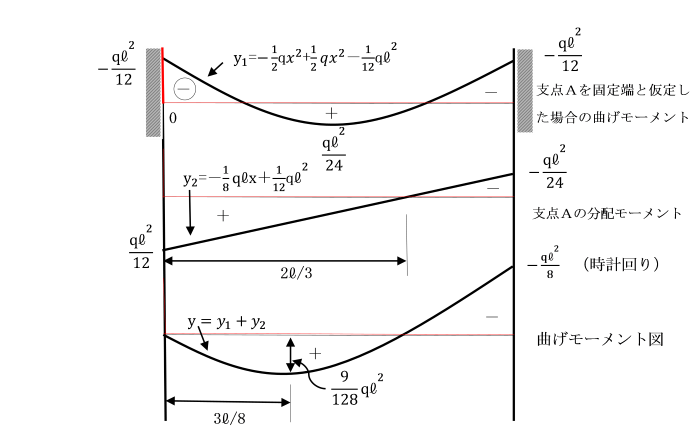
Ap=-ql2/12 (時計回り)となります。
拘束されたはりは、支点Bで回転がないから、
等価構造とするため、支点の回転を考慮した荷重状態を重ね合わせなければなりません。
そこで、図3のように単位の回転をほどこす。
単位の回転を生じさせる剛性影響係数Sは、
S=4EI/l です。
SのD倍と Apの重ね合わせが、実際のはりと等価になることから、
実際の点Bにおける曲げモーメントをMとすると、
M=Ap+D・S が成立します。
実際の点Bにおける曲げモーメントは0ですから、
0=Ap+D・S (反時計回りを正としています。)
したがって、D=-Ap/S=(ql2/12)/(4EI/l) =ql3/48EI となります。
このようにして、節点Bの回転角が決定されます。
Dの値は正ですから、
回転の方向は、反時計回りであることを意味しています。
等価構造を利用することにより、
支点Aの反力を求めることができます。
図2の拘束されたはりの支点Aの反力RA0と
図3の支点Aの反力RA´のD倍との重ね合わせが、
実際のはりの支点Aの反力となります。
実際のはりの支点Aの反力をRA とすると、
RA =RA0+RA´・D が成立します。
RA0=ql/2 、 RA´=6EI/l2 、 D=ql3/48EI より、 RA =5ql/8 となります。
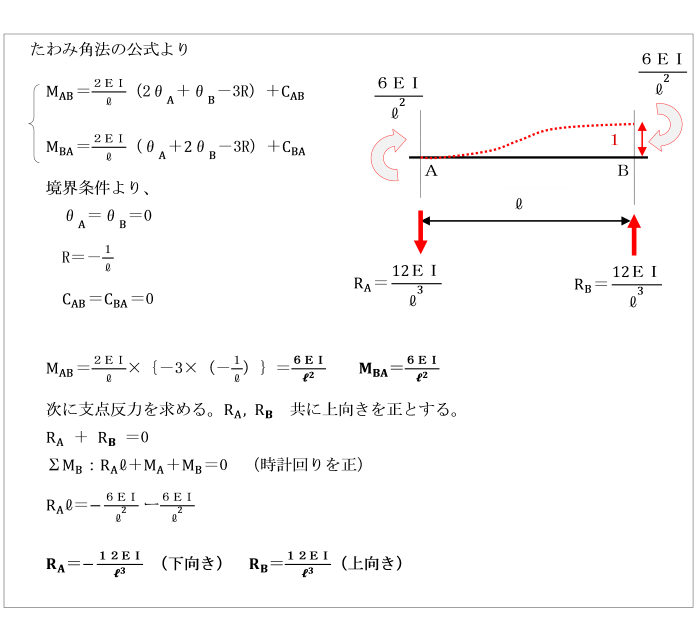
[剛性影響係数の証明]
(1)単位回転を受けた固定ばりの剛性影響係数
両端が回転構造である単純ばりと仮定し、
両端に外力として時計回りのモーメント荷重MA,MBを作用させます。
その際の両端のたわみ角は、
モールの定理より、単純ばりのA点及びB点のたわみ角θA、θBは、
曲げモーメント図を荷重と考えたときの
A点及びB点のせん断力を曲げ剛性(EI)で割ったものに等しい。
モーメント荷重とたわみ角の関係式を用いて、両端固定ばりに適用します。
式を誘導する際、
モーメント荷重は、時計回りを正(たわみ角の正の方向)としています。
※ 最初のモーメント荷重の作用方向の仮定が、時計回りを正としています。
(2)単位の移動を受けた固定ばりの剛性影響係数
【Ⅰ】剛性法により、枕片持ちばりの支点反力、断面力を求めよ。
[枕片持ちばり:再掲]

[解法の手順] A点におけるたわみ角
【手順1】
拘束されていない未知節点変位(支持点及び突出した部材の自由端)を選定し、
その変形を拘束します。(拘束構造の設定)
未知節点変位は、支点Aにおける回転角D(時計回り)のみです。
【手順2】
実際の構造物に全ての未知節点変位が、0になるように構造上の変更を加えます。
支点Aの未知節点変位が、0になるように拘束します。
節点Aを回転しないように拘束するため固定端とします。
【手順3】
拘束構造(両端固定ばり)において、未知節点変位箇所の作用力(断面力、反力)を求めます。
拘束構造におけるA点の曲げモーメントApを求めます。
Apは、未知の節点変位(回転角)Dに対応する作用で、回転角Dと同じ向き、
すなわち時計回りであれば正となります。Apは拘束構造物(両端固定ばり)において反時計回りに作用するため、
Ap=-ql2/12 (反時計回り) となります。
【手順4】
拘束構造から実際の構造と等価になるように構造上の操作を行います。
重ね合わせの原理により、未知節点変位を求めます。
※ 剛性影響係数とは、単位の変位によって引き起こされる作用力(断面力、反力)です。
次に、実際の構造物は、
A点ではたわみ角Dが生じるため、未知の節点変位箇所であるA点において、
単位の回転を与えた固定ばりを設定します。
点Aにおける単位回転による剛性影響係数Sは、
S=4EI/l (時計回り)
【手順5】
実際のはりは、点Aでは曲げモーメントが生じない代わりに回転角Dが生じます。
一方、拘束構造のはりは、点Aで曲げモーメントが生じる代わりに回転角Dが生じません。
つまり、固定端Aに単位の回転角1を作用させ、
それのD倍の回転角を生じさせる部材剛性(曲げモーメント)と、
点Aにおける曲げモーメントの値を重ね合わせたものが、
実際のはりに生じる曲げモーメントになることを利用します。
実際のはりの点Aでの曲げモーメントをMAとすると、
MA=Ap+S・D が成立します。
実際点Aの曲げモーメントは0ですから、
0=Ap+D・S ∴ 0=-ql2/12+4EI/lD より、 D=ql3/48EI となります。
このようにして、支点Aにおけるたわみ角が決定されます。
たわみ角Dが正の符号であるため、
時計方向であることを意味しています。
[解法の手順] B点の支点反力
【手順1】
実際のはりの支点Bの反力RBを求めます。
この力は、図-1に示す拘束構造物の反力RB´と
図-2に示す単位の回転を与えた固定ばりの反力RB0のD倍の和として求めることができます。
反力RBは重ね合わせの原理より、
RB=RB´+RB0・D が成立します。
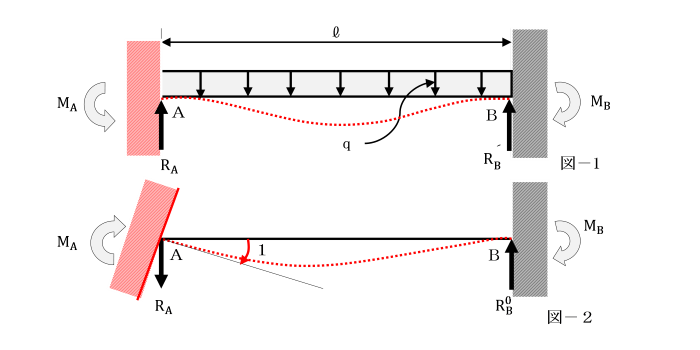
【手順2】
RB´=ql/2 RB0=6EI/l2 (単位の回転を与えた固定ばりの剛性影響係数より)
【手順3】
手順2の結果をRB=RB´+RB0D に代入すると、
RB=ql/2+6EI/l2×ql3/48IE= ql/2+ql/8=5ql/8 となります。
【手順4】
B点の支点反力が得られれば、他の反力、断面力を求めることができます。
RA+RB=qlより、 RA=3ql/8 Mx=3qlx/8-q/2 x2
8.5.2 たわみ角法
【解析原理】
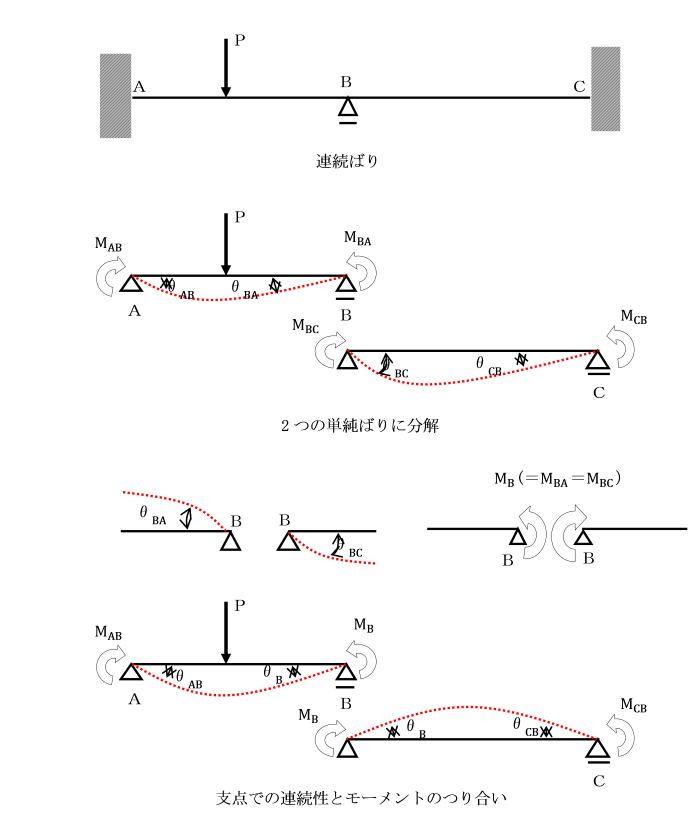
図の不静定ばりを2つの単純ばりに分解し、
モーメント荷重や集中荷重が作用したときの変位を求めます。
そして、この2つの単純ばりをつないで元の連続したはりをつくることを考えます。
その際、2つの単純ばりをつないで連続したはりにするためには、
次の2つの条件を満たす必要があります。
(1) 点Bの左右のたわみ角は、等しくなければならない。
(2) 点Bに大きさが等しく、向きが逆のモーメント荷重が作用しなければならない。
MBA=MBC=MB
さらに、本連続ばりは、A,C両端が固定されてますから、
たわみ角は、
θAB=θCB=0 となります。
これら(1)(2)の2つの条件及びA,C両端のたわみ角が0であるいうことを用いると、
2つの単純ばりをつなげたはりは、元の連続したはりと同じ変形をします。
元の連続ばりの変形は、2つの単純ばりに分解されて表されています。
したがって、3個のたわみ角(θAB=θCB=0 と
θB)の変形条件を満足するように、
3個のモーメント荷重 MAB, MB, MCBを2つの単純ばりの連続性より求めます。
つまり、連続ばりは2つの単純ばりに集中荷重Pと
モーメント荷重 MAB, MB, MCBが作用する問題に置き換えられます。
モーメント荷重の方向
モーメント荷重の向きは、時計回りを正とし、
たわみ角も時計回りを正とする。
部材の両端に作用するモーメントを材端モーメントといいます。
A点に作用する材端モーメントをMAB、
B点に作用する材端モーメントをMBAと表す。
接線回転角
材端モーメントMAB、MBAを受ける単純ばりの両端のたわみ角τA、τBを接線回転角といい、
時計回りを正とします。
部材回転角
モーメント荷重を作用させ、
変形を保ったまま単純ばりをRだけ回転させます。
角度Rを部材回転角といい、時計回りを正とします。
たわみ角と接線回転角及び部材回転角の関係
支点A,Bの相対沈下量⊿がある場合、
水平軸を基準としたA´点,B´点のたわみ角をθA,θBで表す。
時計回りを正とします。
θA=τA+R
θB=τB+R
材端モーメントとたわみ角の関係
図のような単純ばりを考えます。曲げ剛性(EI)は一定とします。
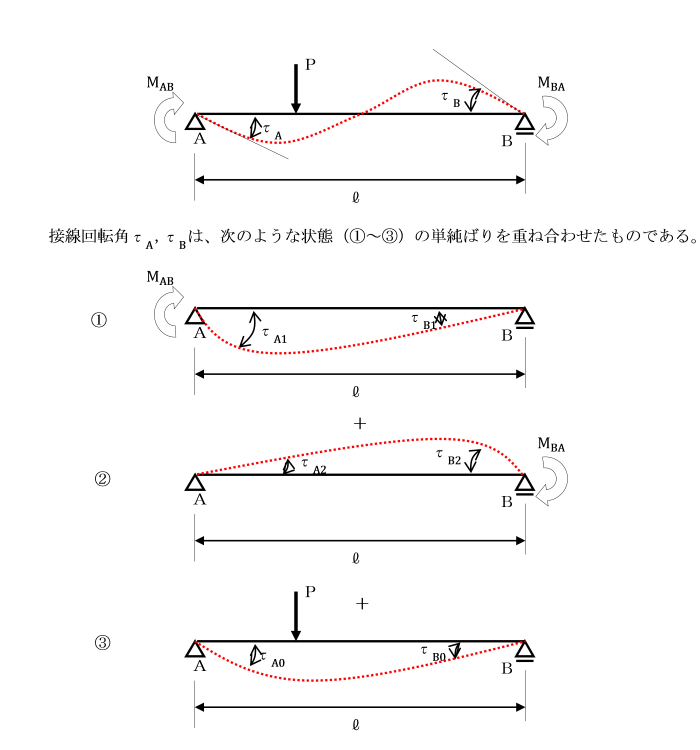
たわみ角法の基本式の誘導(1)
τA1,τB1は、モールの定理(第3定理)を用いて求めることができます。
つまり、τA1,τB1は、単純ばりABに荷重モーメントMABが作用した場合の曲げモーメント図を
曲げ剛性(EI)で割った図形を分布荷重と考え、
この荷重によるA点、B点のせん断力が、たわみ角に等しい。
同様にして、τA2,τB2及びτA0,τB0を求めます。
【モールの定理】(第3、第4定理)
はりに載荷された荷重により曲げモーメント図を曲げ剛性(EI)で割った図形を分布荷重(弾性荷重)と考え、
この荷重による任意点のせん断力、曲げモーメントが、
それぞれたわみ角、たわみに相当します。

これより、荷重項CAB、CBAは、両端固定ばりの支点に生じるモーメント荷重であることが分かります。
この意味で荷重項は、固定端モーメントとも呼ばれます。
図のような集中荷重Pが作用する場合の荷重項の計算を行う。
曲げ剛性(EI)は一定とします。
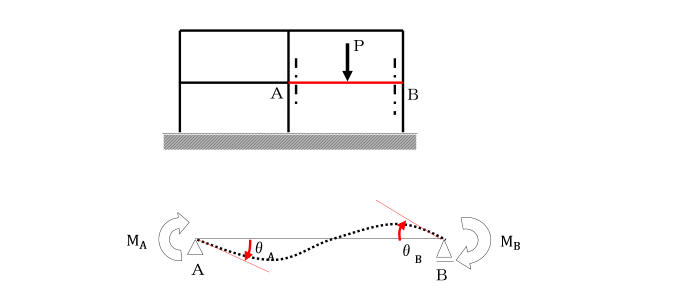
ラーメン構造の1つの直線部材ABを取り出し、
部材ABを単純ばりと考えます。
この単純ばりの左端に時計回りのモーメント荷重MA、
右端にも同様に時計回りのモーメント荷重MBを作用させます。
この式は、はりABに鉛直荷重も作用せず、
両端部の支点にモーメント荷重が作用しているときに、
支点におけるモーメント荷重Mと
たわみ角の関係を表したものです。
次に、この単純ばりの中央に集中荷重Pのみを載荷します。
そのとき部材両端のたわみ角は、
左端(θA)が、+Pl/16EK(時計回り)、
右端(θB)が、-Pl/16EK(反時計回り)となります。
部材ABは両端が、回転支点である単純ばりと仮定しているため、
AB両端には曲げモーメントは生じません。
実際、部材ABは、ラーメン構造として剛節されている訳ですから、
集中荷重Pが作用した場合に、
取り出した部材ABの両端には、
断面力としての材端力が生じています。
今、外力として作用させたモーメント荷重MA 、MBを
集中荷重Pが作用した時に両端に生じる内力として考えます。
そうすると、集中荷重Pの作用により、
部材ABの両端に生じる内力の関係として整理できます。
ABは単純ばりと考えているため、
集中荷重Pによって回転支点ではたわみ角が生じますが、
内力としての曲げモーメントMA 、MBは生じません。
はり中央に集中荷重Pが作用しているときの
A端、B端の曲げモーメントとたわみ角の関係式を表しますと、
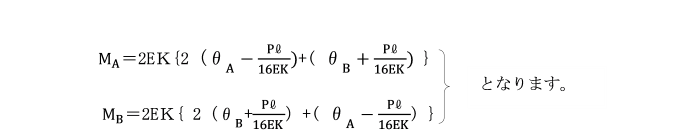
MA 、MBは、外力ではなく、
集中荷重Pによって生じる内力であると考えます。
上式MA 、MBは、θAが、+Pl/16EK、
θBが-Pl/16EKの場合、
MA、MBの値は0となり、
材端モーメントは生じていません。
つまり、両端が回転支点では、
曲げモーメントは生じません。
上式MA,MBを変形しますと、
ここで、上式においてθA=θB=0の場合、
つまり、両端固定ばりの曲げモーメントを示しています。
A点は、反時計回りに材端モーメントPl/8、
B点は、時計回りに材端モーメントPl/8が生じます。
ここで、CAB、CBAは、たわみ角の荷重項と呼ばれるもので、
θA=θB=0
つまり、両端固定端の曲げモーメントに等しい。
また、部材の右端が左端に比べてδだけ低い位置にある場合には、
見かけ上、θA=δ/l、θB=δ/lであっても、
実質的にたわみ角が生じていないため、
材端モーメントMA 、MBには影響しない。
R=δ/l(とう度)として、上式に組み込むと、
となり、たわみ角法における基本式となります。
さらに、任意に選んだ断面2次モーメントIC及び部材長lCによって基準剛度KC=IC/lCを定義すると、k=K/KCを剛比という。Kは、剛度(I/l)。
ここで、
【Ⅱ】 たわみ角法により、枕片持ちばりの支点反力、断面力を求めよ。
[枕片持ちばり:再掲]

[解法の手順]
【手順1】
たわみ角法の一般式に荷重条件、支点の状況を代入し、
必要諸量(θ、M)を求めます。
MA=2EK(2θA +θB-3R)+CAB
MB=2EK(2θB+θA-3R)+ CBA
【手順2】
必要諸量が求まれば、支点反力、断面力を求めます。
① MA=2EK(2θA+θB-3R)+CAB
点Aは可動支点であるため、
MA=0。点Bは固定支点より、θB=0。
また、荷重項CAB=-ql2/12 であるから、
たわみ角法の一般式
MA=2EK(2θA+θB-3R)+CAB にそれぞれの条件を代入すると、
0=2EI/l (2θA+0-0)-ql2/12
4EIθA/l =ql2/12
θA=ql3/48EI θB=0 となります。
次に、
MB=2EK(2θB+θA-3R)+ CBA に、
θA=ql3/48EI、θB=0、CBA=+ql2/12 を代入すると、
MB=2EI/l (2×0 +ql3/48EI+ql2/12=ql2/24+ql2/12=ql2/8 (時計回りの方向)
② 支点反力を求めます。
つり合いの条件式より
ΣV=0 RA+RB-ql=0
ΣMB=0
点Bをモーメントの中心とします。
ΣMB:RA-ql×1/2+ql2/8=0
RAl=ql2/2 - ql2/8=3ql2/8
∴ RA=3ql/8 、RB=ql-3ql/8=5ql/8
MA=0 、 MB=-ql2/8 (上側引張り)
たわみ角法の基本式の誘導(2)
モールの第2定理を用いて、たわみ角法の基本式を誘導します。
【第2定理】
たわみ曲線上の任意の2点における接線が、そのうちの1点をとおる鉛直線から切り取る長さは、
2点間の曲げモーメント図の面積のその鉛直線側の1点に対する
断面1次モーメントを曲げ剛性(EI)で割ったものに等しい。
この定理とともに用いられる符号の規則は、
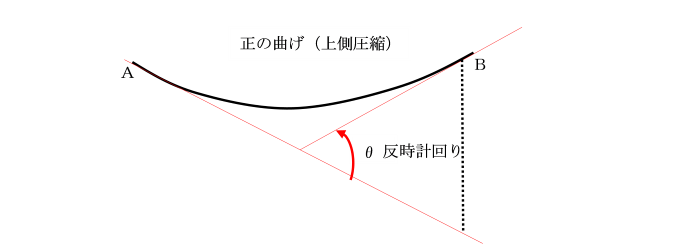
(1)正の曲げモーメントは、はりの上側に圧縮を生じます。
(2)角θは、点Bにおける接線が
点Aにおける接線に対して
反時計回りに回転しているとき正です。
(3)点Aと点Bの間の曲げモーメント図が、
一部は正であり、他は負である場合には、
負の曲げモーメントに対応した面積の部分には、
負の符号をつけなければなりません。
今、部材ABの両端部にモーメント荷重と
その荷重により現位置ABからA´B´に移動したものとします。
このときB´がA´に対して相対的に時計回りの方向に動く場合と
反時計回りに動く場合の二つがあります。
また、A´がB´に対する相対的変位の関係も同様です。
この変位の大きさをdで表します。
A点に作用する材端モーメントをMABで表し、
B点に作用する材端モーメントをMBAで表します。
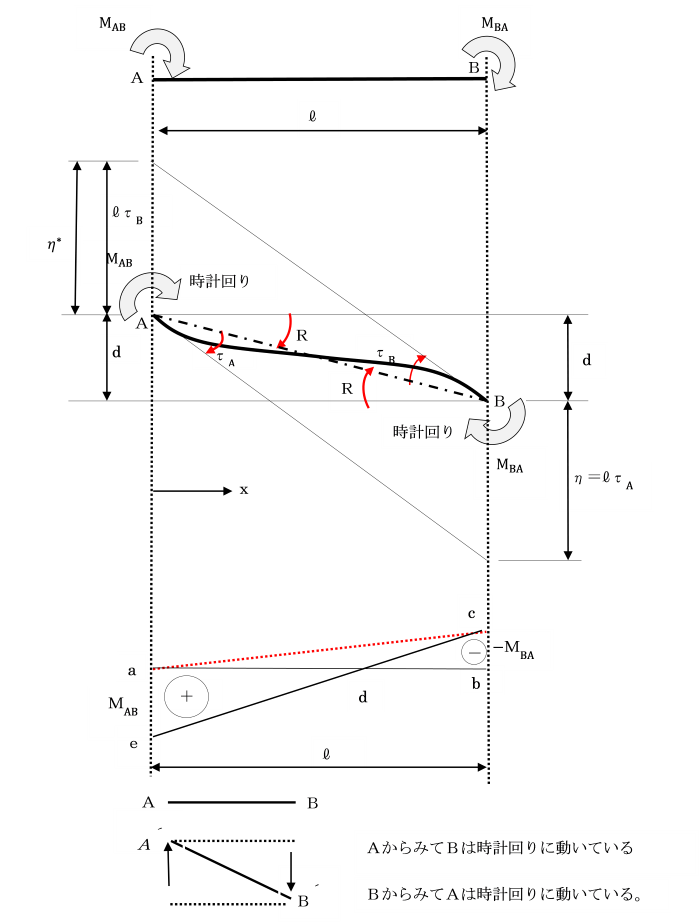
図においてMAB,MBA,τA,τB及びdは、
何れも時計方向であるため、正符号を有します。
図より、A点の接線が、
B点をとおる鉛直線から切り取る長さηは、
η=lτA と表され、
モールの第2定理より、
B点をとおる鉛直線から切り取る長さηは、
三角形adeの面積に、
その重心からBの真下までの距離を乗じたものですから、
三角形bcdの面積に、
その重心からBの真下までの距離を乗じたものを引き、
1/EIを乗ずれば得られます。
このことは、三角形aceの面積に、
その重心からBの真下までの距離を乗じたものから、
三角形bacの面積に、
その重心からからBの真下までの距離を乗じたものを引き、
1/EIを乗じたものと同値です。
したがって、η=+{MAB×(l/2)×(2l/3)-MBA×(l/2)×(l/3)}×(1/EI となり、
+の符号は、点B´が、
点A´における接線よりも上にあることを意味しています。
8.5.3 モーメント分配法
たわみ角法の基本式を利用します。
連続ばり等の支点を固定端に置き換え、
材端モーメントを求めます。
その置き換えた固定端に発生した材端モーメントが、
支点の左右で不つり合いがなくなるまで繰り返し分配し、
逐次近似する数値解析法です。
[モーメント分配法の適用手順]
① 連続ばりの各スパンの支点を固定と仮定し、
与えられた荷重に対する固定端モーメントを求めます。
② 各スパンの支点を固定としたことから、
各支点の左右におけるモーメントには違いが生じます。
すなわち「不つり合いモーメント」が生じます。
③ 実際の連続ばり支点には、
不つり合いの状態にはなっていないため、
各支点に生じている不つり合いモーメントをなくすため、
各支点にこの不つり合いモーメントと同じ大きさで、
逆向きにモーメントを作用させます。
④ ある支点に作用させた逆向きの不つり合いモーメントが、
支点の左右にどのように分配されるか(分配モーメント)を調べます。
さらに分配されたモーメントが、
隣の支点にどのような影響(到達モーメント)を及ぼすか調べます。
⑤ すべての支点で不つり合いモーメントが、
解消されるまで上記の操作を繰り返す。
モーメント分配法を適用するには、
(1)固定端モーメントの算定、
(2)モーメントの分配方法、
(3)有効剛比、
(4)到達モーメントを理解する必要があります。
(1)固定端モーメントの算定
固定端におけるモーメントMA、MBは、次の式から求めることができます。
ただし、はりの下側が引張りとなる曲げモーメントを正(+)とします。
[固定端モーメントの一般式の誘導]
モールの定理を適用して固定端モーメントを求めます。
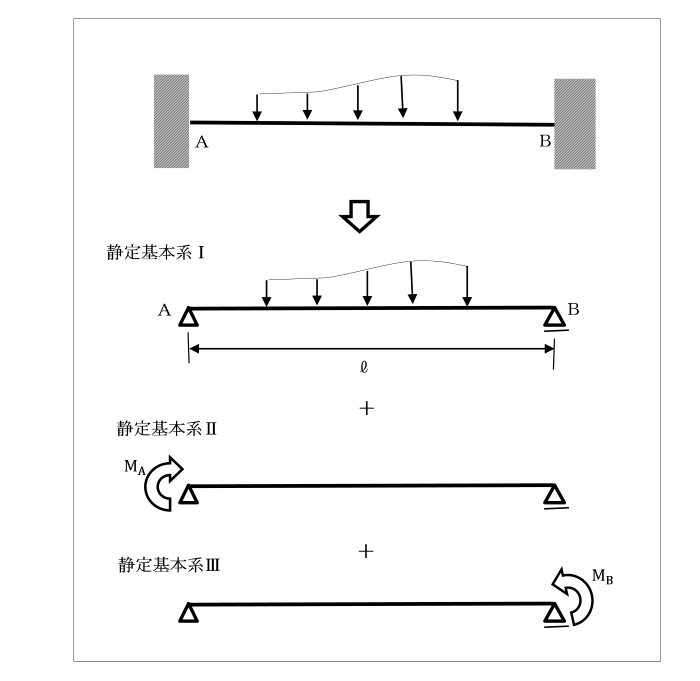
図のような不静定ばりは、
静定基本系Ⅰ、Ⅱ及びⅢに分解することができます。
単純ばりのたわみ、たわみ角を求める場合は、
はりに載荷された荷重による曲げモーメント図を曲げ剛性(EI)で割った図形を分布荷重と考え、
この荷重(弾性荷重)によるせん断力、曲げモーメントが、
それぞれたわみ角、たわみに一致します。
(2)モーメントの分配方法
ある支点にモーメントが作用した場合、
部材に分配されるモーメントは、
それらの剛比に比例します。
剛比によって分けられたモーメントのことを分配モーメントといいます。
ここで注意すべきは、分配モーメントは、
それぞれの部材の剛比kによって振り分けられますが、
正確には、それぞれの部材の有効剛比keの割合により、
分配されることになります。
例えば、図において、AC材とBC材が等質等断面である場合、
断面2次モーメントは同じ値になります。
また、AC材とBC材の長さが同じである場合には、
剛比kは同じ値になります。
しかし、A点とB点の支点の拘束条件が異なる場合は、
同じように扱うことはできません。
支点の拘束状態、つまり、部材の変形の違いによる影響を考慮した有効剛比keを
設定する必要があります。
(3)有効剛比(等価剛比)
剛比は、部材同士の応力を受け持つ強さの比率です。
断面2次モーメントIを、その部材の長さlで割ったものを部材の剛度(K=I/l)といいます。
この剛度を、ある部材を基準として標準剛度(K0)を決め、それで割ったものが剛比となります。
k(剛比)=K/K0
ラーメン、はりの節点(支点)の構造により、
部材の剛比kの代わりに、有効剛比keというものを用いると、
計算過程を短縮することができます。
接合している部材の支点が固定端であれば、
剛比がそのまま有効剛比となります。
有効剛比は、たわみ角法の基本式において、
部材の他端が固定である場合と同じ形の式に
誘導することによって得られます。
[有効剛比算定のための基本式]
モーメント分配法は、連続ばり、ラーメン等の支点(節点)を固定端に仮定して、
支点(節点)上のモーメントを求める方法です。
図のような部材ABのB端が固定である構造を基本としています。
たわみ角法の基本式
Mb=k(2φa+φb+ψ)+Cab
において、固定端の適合条件であるψ=0、Cab=0及びφb=0 より、
Mab=2kφa を有効剛比算定のための基本式とします。
[補足説明]
片持ちばりの先端にモーメント荷重が作用したときには、
曲げモーメント図は、先端から固定端まで一定です。
これは、一方の端部が自由端によるためです。
たわみ角法を連続ばり、ラーメン等に適用する場合、
その支点(節点)にモーメント荷重を作用させており、
決して片持ちばりの自由端にモーメント荷重を作用させている訳ではなく、
一方は回転支点、もう一方は固定端というモデルを想定しています。
そのため支点(節点)にモーメント荷重を作用させた場合、
固定端側に1/2の到達モーメントが発生することになります。
(4)到達モーメント
部材の一端にモーメント荷重が与えられたときに、
それによって生じた他端の曲げモーメントを到達モーメントといいます。
支点を介して分配されたモーメントは、
他端が固定端の場合は、その1/2が伝達されます。
分配モーメントが分かると、他端には付加的なモーメントである到達モーメントが生じます。
モーメント分配法では、連続ばりの各スパンの支点を固定と仮定しています。
そのためある支点にモーメント荷重Mが作用したとき、
他端の固定端モーメントは、同じ向きにM/2のモーメントが伝達されます。
しかし、ラーメン、連続ばりの構造によっては、
有効剛比という考え方を導入すれば、計算の手数が短縮することができます。
その際、到達モーメントがM/2ではなくなることに留意する必要があります。
連続ばりを例にとり、解法原理を説明しましょう。
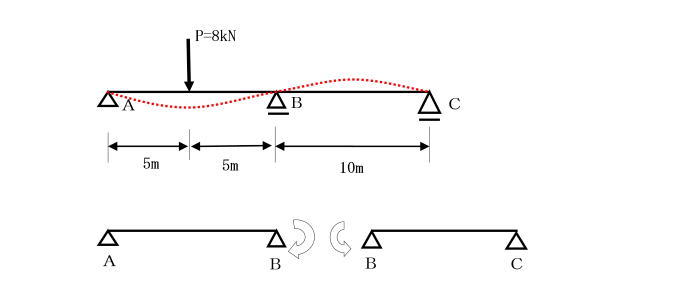
【例題1】 図の連続ばりをモーメント分配法により、モーメント図を描きなさい。
ただし、曲げ剛性(EI)は一定です。
[解法の手順]
支点A,C及び中間支点Bにはたわみ角が生じます。
[有効剛比を用いない場合]
① 連続ばりの各スパンの支点を固定と仮定し、
与えられた荷重に対する固定端モーメントを求めます。
はりABの中央に集中荷重Pが作用していることから、
点A,Bの固定端モーメント TA,TBはそれぞれ、
TA=-Pl/8=-8×10/8=-10(反時計回り)
TB=Pl/8=8×10/8=10(時計回り)
② 各スパンの支点を固定と仮定したことから、
各支点の左右のモーメントには違いが生じます。
すなわち「不つり合いモーメント」が生じます。
点Aは、TA=-Pl/8=-8×10/8=-10
点Bの左側は、TB=Pl/8=8×10/8=10 右側は、0となっています。
③ 各支点に生じている不つり合いモーメントをなくすため、
各支点に、この不つり合いモーメントを逆向きに作用させます。
実際、連続ばりの支点Aはヒンジであるため、
モーメントは生じません。
それを打ち消すため、
固定端モーメントTA と大きさが等しく、向きが反対の外力モーメントTA1=10を作用させます。
④ 点AにTA1=10を作用させたことにより、
点Bは固定端と仮定していますから、
到達モーメント 1/2×TA1=5(時計回り)が伝達されます。
⑤ 次に、点Bでの不つり合いモーメントを解消するため、
固定端モーメント-15[-10+(-5)]と大きさが等しく、
向きが反対の外力モーメントTB1=15を点Bに作用させます。
はりBA、BCにそれぞれの剛比の割合で分配され、
支点A、Cには到達モーメントとしてそれぞれの1/2が伝達されます。
⑥ 再度、支点A,Cに生じている不つり合いモーメント(点Bからの到達モーメント)をなくすため、
それと大きさが等しく、向きが反対の外力モーメント+3.75、-3.75をそれぞれ支点A,Cに作用させます。
以上の計算過程から、図(A),(B),(C),(D)の曲げモーメント図を
重ね合わせたものが連続ばりの曲げモーメント図となります。
支点A,Cの不つり合いモーメントが解消されます。
[有効剛比を用いた場合]
① 部材AB、BCにおいて、支点Bは固定と仮定します。
他端A、Cはヒンジですから、有効剛比ke=3/4・kを用います。
部材ABには中間荷重が載荷されているため、
支点Bの左右におけるモーメントには違いが生じます。
すなわち「不つり合いモーメント」が生じます。
支点Bの左側は、HBA=3Pl/16=3/16×8×10=15(時計回り)。右側は、0となります。
部材AB部分を取り出して考えます。
支点Bは固定端と仮定していますから、
図のような枕片持ちばり(1次不静定ばり)となります。
固定端Bの曲げモーメントは、HBA=15(時計回り)ですから、
支点反力RA、RBは、
つり合い条件式より求めることができます。
支点Bをモーメントの中心とすると、
ΣMB:RA×10-8×5+15=0
∴ RA=5/2 、RB=8-5/2=11/2
曲げモーメントの一般式は、次のようになります。
0≦x≦5 Mx=5/2x
5≦x≦10 Mx=5/2x-8(x-5)=-11/2x+40
② 支点Bには外力モーメントは作用していませんから、
支点Bのモーメントの和は0にならなければなりません。
そこで、支点Bに生じている不つり合いモーメントをなくすため、
これと大きさが同じで逆向きもモーメントを作用させます。
-TB=-HBA=-15
はりBA、BCに、それぞれの有効剛比の割合で分配されます。
また、支点A、Cはヒンジのため、
到達モーメントは0となります。
部材BAの分配モーメントMBA=(3k/4)/(3k/4+3k/4)×(-TB)
=0.75/1.5×(-15)=-7.5
部材BCの分配モーメントMBC=(3k/4)/(3k/4+3k/4)×(-TB)
=0.75/1.5×(-15)=-7.5
以上の計算過程から、図(A),(B)を重ね合わせたものが、
曲げモーメント図となります。
有効剛比を用いると、計算の手数をかなり短縮できることが分かります。
【例題2】 図の連続ばりをモーメント分配法により、モーメント図を描きなさい。
ただし、曲げ剛性(EI)は一定です。
【Ⅲ】モーメント分配法により、枕片持ちばりの支点反力、断面力を求めよ。
[枕片持ちばり:再掲]

[解法の手順]
【手順1】
連続ばりの支点Aを固定端と仮定し、
与えられた荷重に対する固定端モーメントを求めます。
点A,Bの固定端モーメントTA 、TBは、それぞれ、
TA=-ql2/12 TB=ql2/12
【手順2】
支点Aを固定としたことから、
支点の左右のモーメントには違いが生じます。
すなわち「不つり合いモーメント」が生じます。
不つり合いモーメントをなくすため、
大きさが同じで逆向きのモーメントTA1=ql2/12を作用させます。
実際、点Aはヒンジであるため、曲げモーメントは生じません。
【手順3】
支点Aに作用させた逆向きの不つり合いモーメントが、
支点Bにどのように分配されるか(分配モーメント)を調べます。
さらに分配されたモーメントが、隣の支点にどのような影響(到達モーメント)を及ぼすか調べましょう。
TA1=ql2/12を作用させたことにより、
点Bには到達モーメント1/2×TA1=1/2×ql2/12が伝達されます。
【手順4】
支点反力を求めます。
つり合いの条件式より
ΣV=0 RA+RB-ql=0
ΣMB=0
点Bをモーメントの中心とします。
ΣMB:RAl-ql×1/2+ql2/8=0 (時計回りを正とする)
RAl=ql2/2 -ql2/8=3ql2/8
∴ RA=3ql/8 、RB=ql-3ql/8=5ql/8
MA=0 、 MB=-ql2/8 (上側引張り)
8.5.4 カスティリアノの第1定理
構造物は弾性的にふるまうため、
外力を作用するときと除去するときの間で、
エネルギーの損失はないものと考えます。
外力による仕事と内力による仕事の大きさは等しい。
これはエネルギー保存の法則と呼ばれます。
カスティリアノの定理を理解するために、
まず外力による仕事と内力による仕事について考えましょう。
(1)仕事とその性質
構造解析では、仕事という概念は重要な役割をはたします。
構造物に外力が作用すれば、
外力の作用点は変位するから、外力は仕事をします。
これを、外力による仕事という。
一方、外力が作用すると、
変位に起因して部材内部には変形が生じ、
同時に構造物内部には応力が生じます。
構造物内部で応力が変形に対して行う仕事を、
内力による仕事という。
内力による仕事はひずみエネルギーとして構造物内に蓄積されます。
ひずみエネルギーは、仕事をする潜在的な能力を持っているため、
ポテンシャルエネルギーとも呼ばれます。
構造物は弾性的にふるまうため、
外力を作用するときと除去するときの間で、
エネルギーの損失はないものと考えます。
外力による仕事と内力による仕事の大きさは等しい。
これはエネルギー保存の法則と呼ばれます。
弾性体内で、応力-ひずみの関係が、
σ=E・εのように線形になっているものを、
線形弾性体という。
また、ゴムなどの高分子材料は、
応力-ひずみの関係が非線形であるが、
応力とひずみの関係は1対1です。
このようなものを非線形弾性体という。
(2)外力の仕事
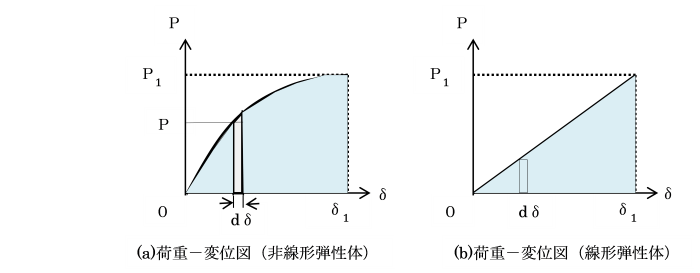
図のように荷重P-変位δの関係(a)にある非線形弾性体の構造物を考えます。
変位が0からδ1に変化する途中に微小な変位dδをとり、
荷重Pが作用すると、
荷重Pによる仕事dWは、
dW=P・dδ
となります。dδは荷重Pが作用している方向に生じているとします。
すると、変位が0からδ1まで増加する間に荷重Pが行う仕事は、
となり、これは、荷重Pが変位δの関数として変化する場合の外力による仕事で、
荷重-変位図の下方にある面積に相当します。
もし構造物が図(b)に示す線形弾性体で、
変位δに比例して荷重Pが作用する場合には、
外力の仕事Wは、
W=1/2 P1・δ1 となります。
ここで注意すべきことは、
右辺に1/2という係数がついていることです。
これは、弾性体に荷重を作用させて変形させる際に、
物体に振動を与えないように、
荷重を0から徐々に加え始め、
最終値にまで増大しているからです。
荷重―変位図の下方にある面積に相当します。
(3)内力の仕事
物体が仕事を行う能力を有するとき、
その物体は、エネルギーを有します。
ひずみが生じた物体が有するエネルギーのことをひずみエネルギーという。
ひずみエネルギーの大きさは、
ひずみが生じた物体が元の状態、
つまり、無ひずみ状態に復帰するまでに行う仕事量によって表されます。
内力の仕事は、ひずみエネルギーとして構造物に蓄えられます。
代表的な変形に対して、
外力の仕事と内力による仕事(ひずみエネルギー)を求めてみましょう。
(4)モーメント荷重を受けるはりの外力仕事と内力仕事
[外力による仕事]
図に示すように、
両端にモーメント荷重Mを受けて、
曲げ変形をするときの外力による仕事を求めます。
モーメント荷重Mによるはりの変形量は、
回転角θで表され、
Mとθの関係は、荷重-変位図に示すように直線0aで表されます。
回転角が0からθ1に変化する途中に微小な回転角dθをとり、
モーメント荷重Mが作用すると、
モーメント荷重Mによる仕事は、
斜線部分の長方形の面積 M・dθ となります。
[内力(ひずみエネルギー)による仕事]
微小要素の体積をdV(=dxdydz=dAdx)とすれば、
微小要素内に蓄えられるひずみエネルギーdUは、
dU=(1/2)σεdV となります。
この式そのものが既にモーメント荷重Mが、
0から徐々に増加して最終値M1に至るまでの微小要素内に蓄えられるひずみエネルギーです。
モーメント荷重を受けるはりの微小要素のyz面に生じる応力は、
y軸の位置によって変化するため、
σ及びεには以下の式を代入する必要があります。
σ=(M1/I) y ε=σ/E=(M1y)/EI dU=(M12/(2EI2) y2dAdx となります。
[カスティリアノの第1定理の誘導]
構造物のひずみエネルギーUは、
荷重によってなされる外力仕事に等しい。
ひずみエネルギーUは、
各々の力Piとそれに対応する変位δiの関数として表されます。
今、一つの変位δiが、
小さい量dδiだけ増加し、
他のすべての変位が、
一定に保たれているときのひずみエネルギーの増加について調べてみます。
ひずみエネルギーの増加dUは、
dU=∂U/(∂δi )・dδi で表されます。
偏微分係数∂U/∂δiは、ひずみエネルギーUのδiに関する変化の割合です。
また、変位δiが、小さい量dδiだけ増加したとき、
仕事は対応する力Piによってなされます。
しかし、他の力は、他の変位が一定に保たれている状態であるため、仕事をしない。
この仕事Pidδiは、構造物の中に蓄えられたひずみエネルギーの増加相当分dUに等しい。
dU=Pidδi
したがって、
∂U/(∂δi )・dδi=Pidδiとなり、
Pi=∂U/∂δi という関係を得ます。
この式は、ひずみエネルギーの任意の変位δiに関する偏微分係数は、
それに対応する力Piに等しいことを示しています。
この式をカスティリアノの第1定理と呼んでいます。
非線形構造物にも適用できます。
【例題1】 次の枕片持ちばりの中央点のたわみをカスティリアノの第1定理により
求めよ。
ただし、はりの曲げ剛性(EI)は一定とします。
カスティリアノの第1定理を適用するための必要な諸量は分かっているものとします。
トップページ