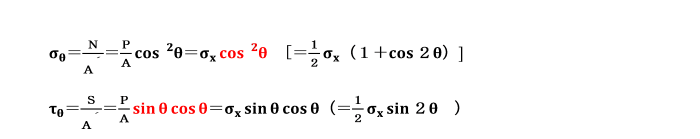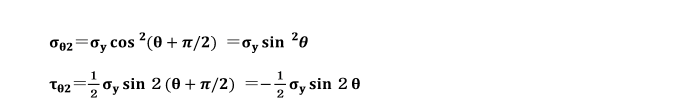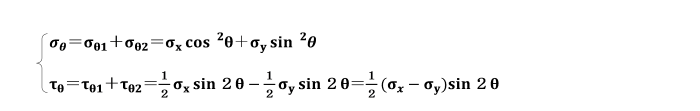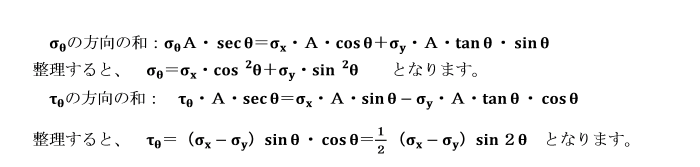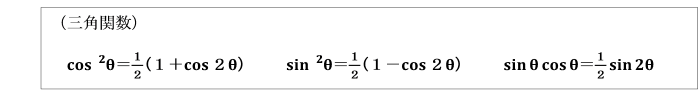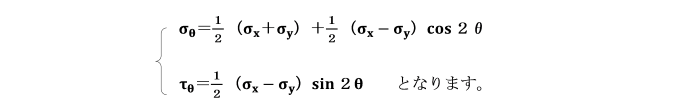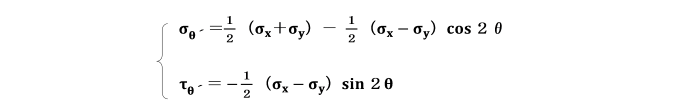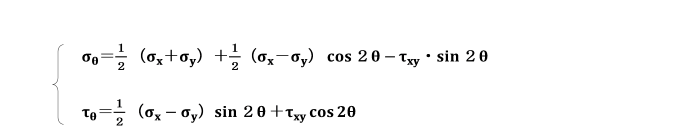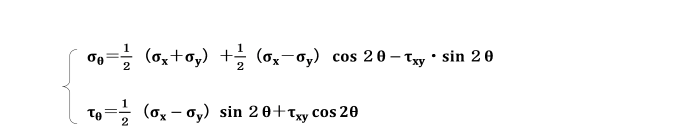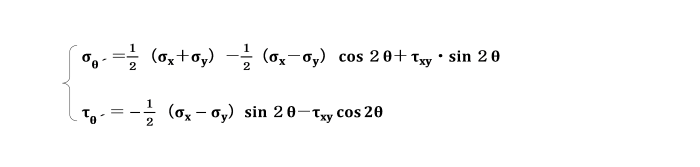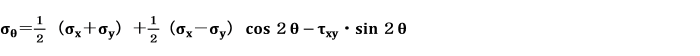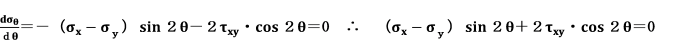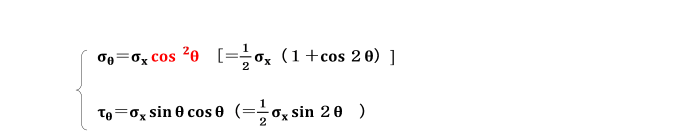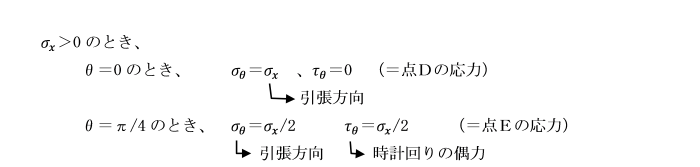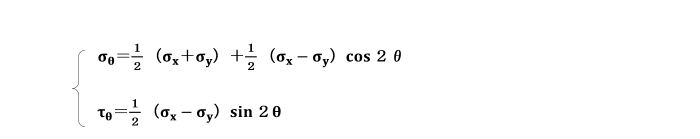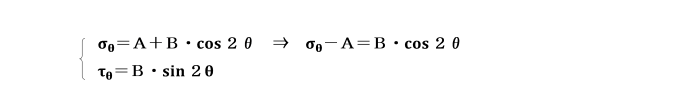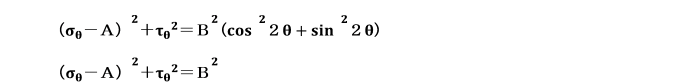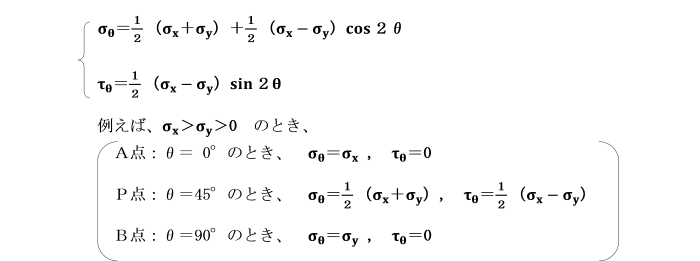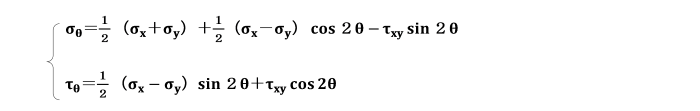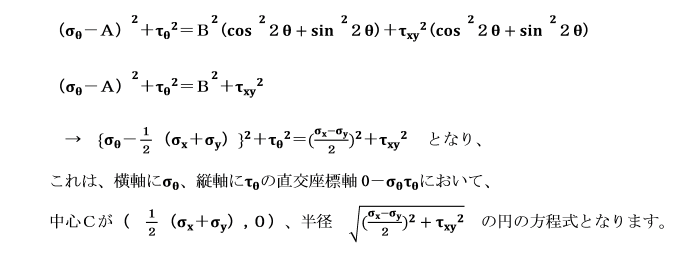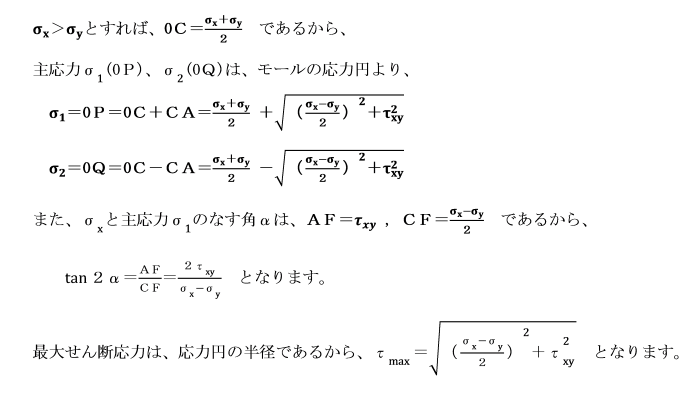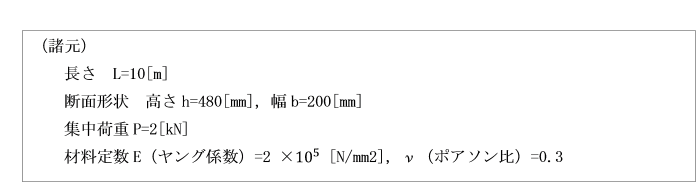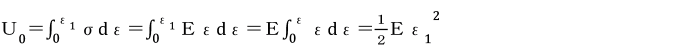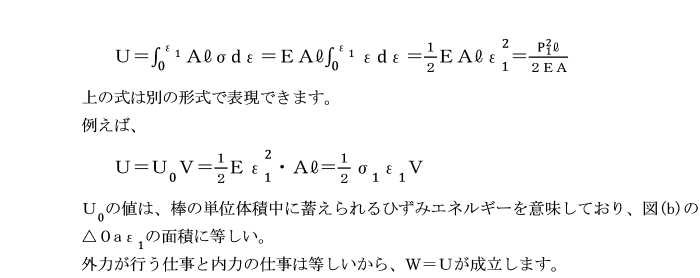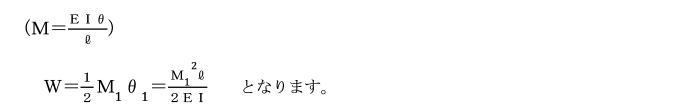トップページ
第7章 はりの応力と影響線
7.1 はり内部の応力
7.1.1 応力の表示法
応力成分を表す文字は、
構造力学では一般的に垂直応力はσ(シグマ)、
せん断応力はτ(タウ)を使用します。
応力の成分を表すために下付きの添字2つを使用します。
1番目の添字は、応力が生じている面を指定し、
2番目の添字が応力が生じている方向を示しています。
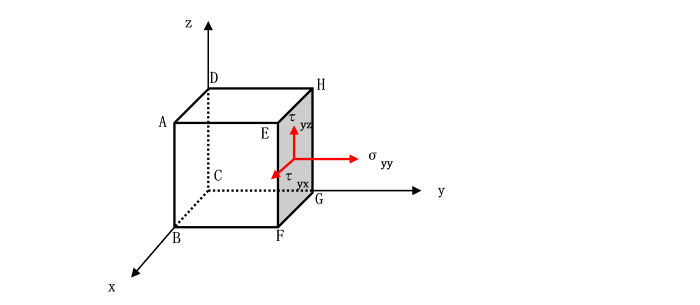
例えば、σyy は、y 軸に垂直な面に生じ、
y 軸方向であることを示しています。
τyzは、y軸に垂直な面に生じ、
z軸方向に生じている応力です。
面に平行な方向に生じていることから、せん断応力です。
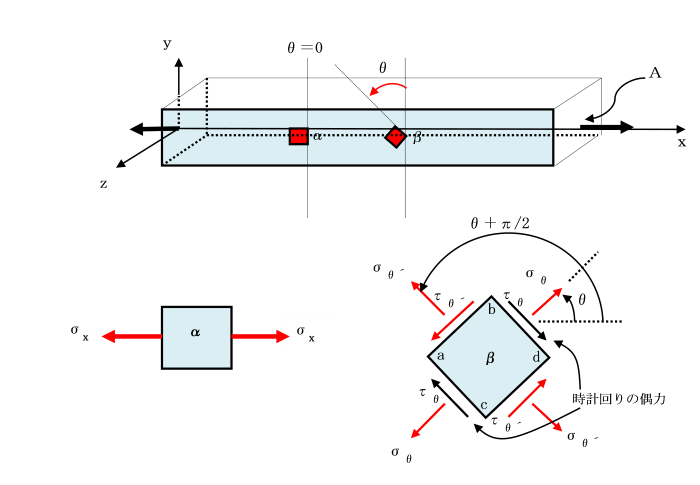
6面体の各面に生じている応力を考えます。
6面体では、y 軸に直交する面は、面EFGHと、
それと向かい合う面ABCDの2つがあります。
この2つの面上に生じる応力成分は、
σyy,τyx,τyzです。
2番目の添字は、その応力が生じている座標方向を示すものであり、
それが例えばy 軸の正の方向に生じているのか、
あるいはy軸の負の方向に生じているのかは明らかでありません。
生じている向き(座標軸の正の方向か負の方向か)を明らかにする手段として、
応力の正負を約束しています。
7.1.2 応力の正負の約束
各座標軸に垂直な面から作られている6面体を考えます。
6面体のある面を考えたとき、
その面に立てた外向き法線つまり、
6面体の外に向かう垂線が座標軸の正(負)の向きを向いているとき、
応力の値を正とします。
例えば、応力成分の値が
σyy=50MPa、τyx=-30MPa、τyz=40MPa の場合を考えてみます。
最初の添字が全てy であるので、
この3つの応力成分はy軸に垂直な面上に生じていることを意味します。
y軸に垂直な面は、面EFGHとそれに向かい合う面ABCDです。
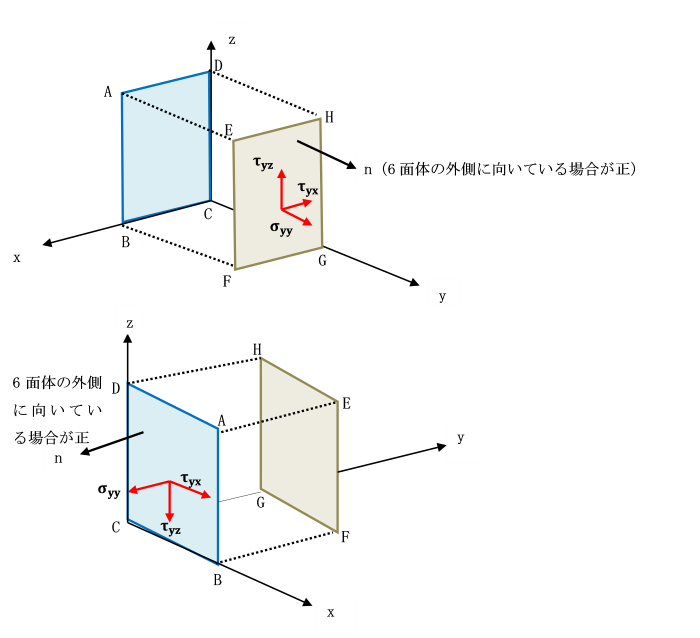
まず面EFGH上で考えてみます。
この面に立てた外向き(6面体の外側に向いている)法線nは、
y軸の正の方向を向いています。
したがって、応力の正負の約束より、正です。
τyx は、x軸の正の方向に生じているものが正です。
今、τyxの値は-30MPa であり負ですから、
その方向はx軸の負の方向です。
一方、σyy は50MPa で正ですから、
その方向はy軸の正の方向です。
同様に、τyz は30MPa で正ですから、
その方向はz軸の正の方向です。
これら応力の生じる向きを図に示す。
次に面EFGHに向かい合う面ABCD上では、
σyy=50MPa、τyx=-30MPa、τyz=40MPa が、
どちらの向きに生じているか考えてみます。
面ABCDに立てた外向き(6面体の外側に向いている)法線nは、
y軸の負の方向を向いています。
したがって、座標軸の負の方向に生じている応力が正です。
σyy及びτyzは、いずれも正の値ですから、
その方向はy 軸及びz軸の負の方向に生じています。
一方、τyx は-30MPa で負ですから、
その方向はx軸の正の方向です。
これら応力成分の方向を図に示す。
これらを比較してみると、向かい合う面の間では、
各応力成分の生じている方向は、
お互い逆向きです。
したがって、向かい合う面の間では、
その面上に生じているx、y、z軸方向の応力は、
お互い方向が逆で、大きさが等しいことが分かります。
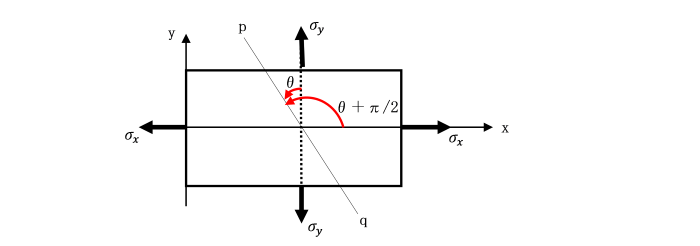
7.1.3 弾性体内の応力(傾斜面上の応力)
これまではりの断面力は、
軸に垂直な断面か、水平断面に生じている応力について考えてきました。
ここでは、はり内部の任意傾斜断面に生じる応力について調べます。
[引張力または圧縮力を受ける棒の内部応力の状況【一軸応力(単軸応力)】]
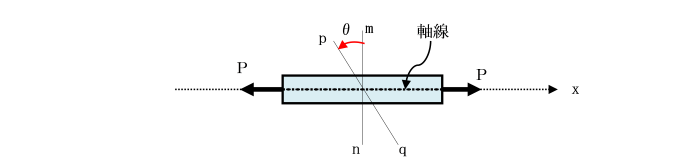
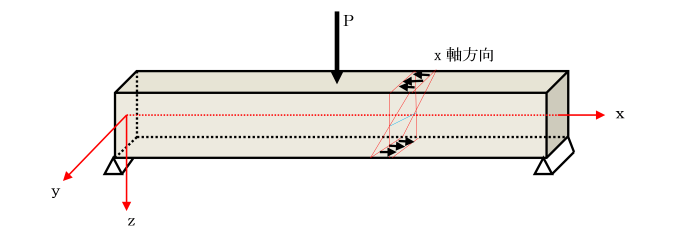
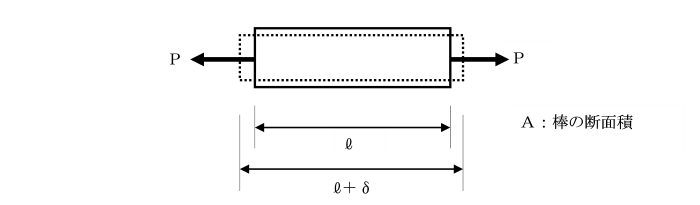
断面積Aの棒が、両端に外力Pを受けて平衡状態にあります。
今、断面m-nで仮想的に切断します。
棒が左右に分離しないで、元の位置に留まっているためには、
断面m-nには外力Pに対抗する力、いわゆる内力が生じています。
この力は、断面上に一様に分布していると仮定します。
単位面積当たりの内力を応力といい、ギリシャ文字σ(シグマ)で表します。
外力Pとそれに抵抗する力σ・Aは大きさが等しく、向きが反対であることが分かります。
したがって、次のような関係式が得られます。
P=σ・A ⇒ σ=P/A
ここで、注意すべきは、σ=P/Aが成立するためには、
外力Pが断面積の図心をとおり、
軸線に平行に作用したときに実現されます。
荷重が図心に作用しないで偏心しているとき、
あるいは図心に作用していても傾斜して作用している場合は、
棒に曲げが生じ、断面上に応力は一様に分布しません。
棒が単純引張りを受けています。
このときの横断面m-nと反時計回りに角θをなす傾斜した断面p-q上の応力を考えます。
棒の左側の部分に作用している外力Pと、
傾斜した断面上p-qに分布する力の合力Rは、
平衡状態にあるため等しい。
合力Rは、断面p-qに垂直な成分Nと平行な成分Sに分解することができます。
これらの成分はそれぞれ、 N=Pcosθ S=Psinθ となり、
三角関数の1次式になります。
傾斜した断面の面積A´は、A/A´ =cosθより、A´=A/cosθ ですから、
N及びSに対応する応力σθ、τθは、それぞれ、
となり、いずれも三角関数の2次式となります。
σx=P/A は、棒の軸線xに垂直な断面上の応力です。
今一度、合力Rを傾斜断面上で分解した垂直成分Nと平行成分Sの式をみますと、
N=Pcosθ,S=Psinθ は、傾斜断面の角度θが変われば、
作用する力N,Sの方向が変わるだけで、力N,Sの合成は合力Rに等しい。
一方、応力を表す式 σθ=N/A´ =σxcos2θ τθ=S/A´=σxsinθcosθ は、
傾斜断面上の単位面積当たりの内力、いわゆる応力を求めたもので、
傾斜断面の角度θが変わると、
作用する力の方向及び傾斜断面の面積の2つが同時に変化します。
このことが、「力」と「応力」との大きな違いとなり、「ベクトル」と「テンソル」の違いとなります。
ベクトルとテンソル
大きさだけでなく、方向と向きをもつ量をベクトルといいます。
変位、力、速度、加速度等は、ベクトル量です。
ベクトルが大きさと方向だけで決まるのに対して、
さらに、そのベクトルが作用する面の大きさも考慮しなければならない物理量がテンソルです。
ベクトルの座標変換式が三角関数の1次式になるのに対して、
テンソルは2次式となります。これは作用面の面積及び垂直ベクトルの方向も関係してくる結果です。
テンソルの具体例としては、応力があります。
応力は、単位面積当たりの内力であるため、作用面の面積と力の方向の2つが変化するという特徴があります。
傾斜した面p-q上の垂直応力σθ及びせん断応力τθは、断面上に一様に分布しています。
垂直応力σθは、θ=0の時は、面p-qは横断面m-nと一致し、
σθ=σxとなります。
θが反時計回りに0から増大するにつれて、応力σθは、P/Aから減少して、
θ=π/2のときには0となり、垂直応力は生じません。
このようにして垂直応力の最大値はθ=0の時に生じ、σmax=σx となります。
一方、せん断応力τθは、θ=0及びπ/2のとき0であり、sin2θ=1のとき、
つまりθ=π/4のとき、最大値に達し、τmax=σx/2 となります。
垂直応力とせん断応力の各々に対し、符号の取り決めをしています。
正の垂直応力σθは、材料の表面から離れる向きに生じ、
負の垂直応力は、材料の表面に向かう方向に生じています。
また、せん断応力τθは、材料の表面に関して時計回りの方向に生じているときを正とし、
反時計回りの方向に生じているときを負とします。
今後は、構造力学の符号の約束により、説明を進めていきます。
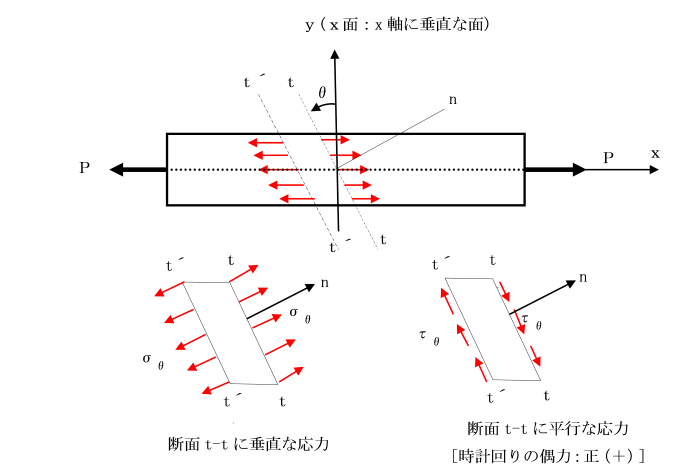
[棒の中の応力状態]
棒をx面(x軸に垂直)から反時計回りにθだけ傾斜した面、tt及びt´t´を考えます。
この面で仮想的に切断して取り出します。
引張力Pが作用している棒を考えます。
2つの断面に生じている応力を傾斜断面に垂直なn方向と平行な方向に分解します。
すると、それぞれ図のようにσθとτθになります。
x面から反時計回りにθだけ回転させた場合、せん断応力τθは、
断面t´-t´に対し断面t-tを時計回り(+)に滑らすように生じています。
次に断面t-tに垂直な断面s-s上の垂直応力σθ´、せん断応力τθ´を
傾斜断面に垂直なn´方向と平行な方向に分解します。
すると図のようにσθ´とτθ´になります。
x面から反時計回りにθ+π/2だけ回転させた場合、
せん断応力τθは、断面s-s´に対し断面s-sを反時計回り(-)に滑らすように生じています。
このように、断面t-t,t´-t´及びs-s,,s´-s´で囲まれた部分に正方形ができます。
この面上に生じる応力は、図に示すようになります。
4辺に生じる各々のせん断応力は等しい。
辺bd,caに生じるせん断応力は、時計回りの偶力を生じるので正(+)、
辺ba,cdに生じるせん断応力は、反時計回りの偶力を生じるので負(-)となります。
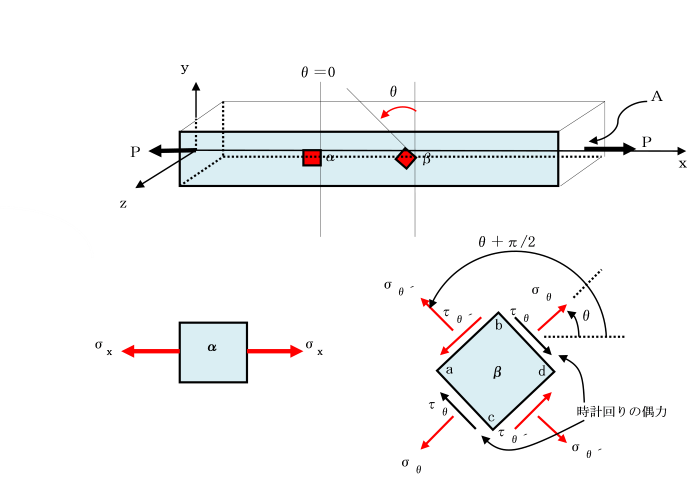
また、下図は棒の中の要素α及びβを取り出したものです。
要素αは、θ=0の位置のものであり、
辺上に作用する応力は、σx=P/Aだけです。
第2の要素βは、反時計回りにθだけ回転したものであり、
要素の面b-d上の応力は、σθ=σxcos2θ 、τθ=1/2 σxsin2θ から計算されます。
s-sに平行な要素の辺a-bに生じる垂直応力σθ´、せん断応力τθ´は、
その垂線がx軸とθ+π/2の角をなしているから、
この面上の応力はσθ,τθ式のθにθ+π/2を代入することによって求めることができます。
要素の面a-b上のせん断応力τθ´は負です。
これは上の図のように要素の面に関して、反時計回りの方向に生じていることを意味しています。
ここで、σθとσθ´、τθとτθ´、に着目すると、
直角をなす2面の応力の間には、
次の関係が得られます。
σθ+σθ'=σx (cos2θ+sin2θ) =σx τθ=-τθ'
σθ+σθ'=σx式から、引張を受けている棒は、互いに直交する2平面上の垂直応力の和は一定でσxに等しい。
τθ=-τθ' 式からは、互いに直交する2平面上のせん断応力は、
その大きさが等しく、符号が反対であることを示しています。
同じように考えると、残りの2面a-c及びc-d上の応力も求めることができます。
a-c上では、θ+πを、c-d上では、θ+3π/2(あるいはθ-π/2)を
σθ=σxcos2θ 、τθ=1/2σx sin2θ 式のθに代入することによって求めることができます。
b-d、a-cに生じるせん断応力の符号は、
時計方向の偶力を生ずるので正、a-b、c-dに生じるせん断応力は、
反時計方向の偶力を生ずるので負となります。
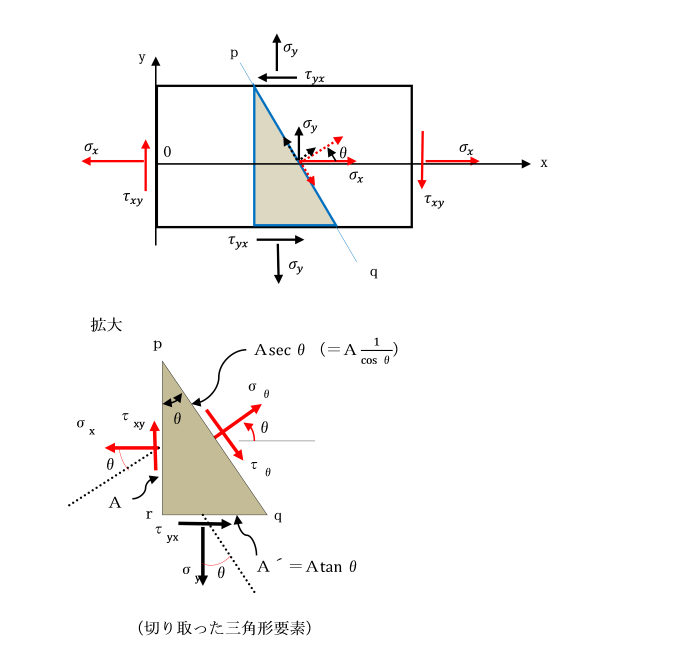
[ニ軸応力を受ける場合の傾斜断面上の応力状態]
外力の作用により、弾性体内の長方形要素に垂直応力σxが、
x面(x軸に垂直)、σyがy面(y軸に垂直)の2方向に生じている状態を考えます。
この状態をニ軸応力状態といいます。
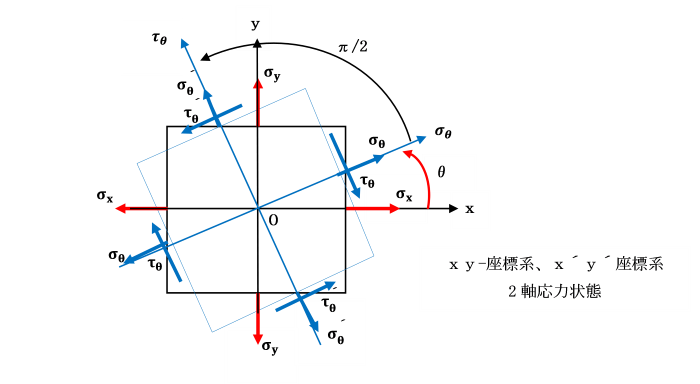
x軸と角θをなす反時計回りに傾斜した面上の断面p-qを考えます。
傾斜した面上に生じる垂直応力σθ及びせん断応力τθは、
先の「引張力または圧縮力を受ける棒の内部応力の状況」で算出した式を活用することができます。
つまり、外力の作用によりx面及びy面に生じている垂直応力σx、σyが、
x面から反時計回りにθ傾斜した断面p-qでの応力状態を考えます。
具体的には、x面に生じている垂直応力σxが、断面p-qではどのような応力状態になっているのか、
y面に生じている垂直応力σyが、断面p-qではどのようになっているのかを考え、
各々の垂直応力及びせん断応力を合成することによって得られます。
今、x面の垂直応力σxが、断面p-qでの応力状態をσθ1、τθ1とすると、
y面の垂直応力σyが、断面p-qでの応力状態をσθ2、τθ2とすると、
となり、断面p-q上の垂直応力σθ、せん断応力τθは次のようになります。
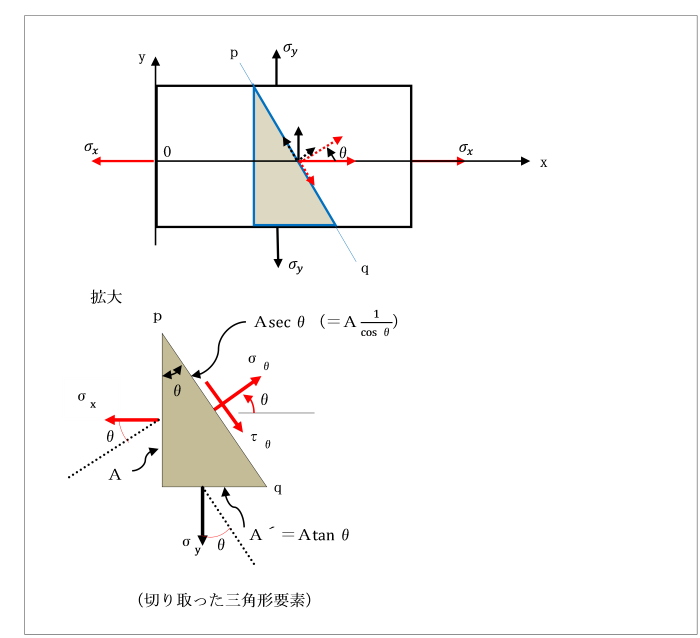
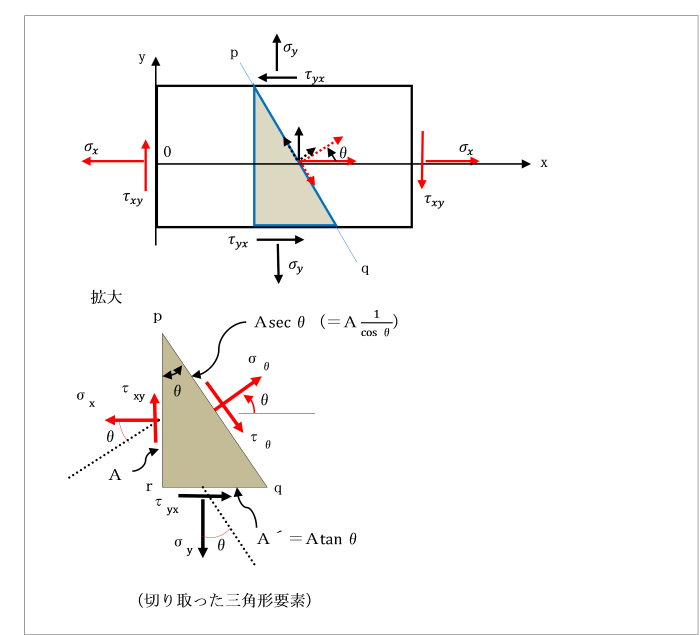
また、長方形要素から切り取った三角形要素が、平衡状態にあることを利用して、
傾斜した面上に生じる応力を求めることもできます。
傾斜した面上に生じる応力は、
垂直応力σθとせん断力τθです。
ここでτθの方向は、はり内部の応力表示法の約束により時計回り(正の方向)に仮定しています。
切り取った三角形要素は平衡状態にありますから、
σxが生じている要素のx面の面積をAとすれば、
要素のy面の面積はA・tanθで与えられます。
また、傾斜した面の面積はA・secθとなります。
したがって、x面上の力はσx・A、y面上の力は、σy・A・tanθとなります。
これらの力は、それぞれ傾斜した平面p-qに垂直に作用する成分と、
平行な成分に分解することができます。
これらの方向の力の和をとれば、
三角形要素の平衡状態に対する2つの方程式が得られます。
σx>σy>0 のとき、θが0≦θ≦π/2 のときには、
τθの値は正となり、先に仮定したとおり、
傾斜面上のせん断応力が、時計回りの方向に生じていることを意味します。
これらの式より、垂直応力σx及びσyを用いて、
任意の傾斜した面上の垂直応力σθ及びせん断応力τθを求めることができます。
また、次の三角関数間の関係式を用いることにより、
また、θの代わりにθ+π/2を代入すれば、
σθ及びτθが生じている傾斜面に垂直な平面に生じている応力σθ´及びτθ´の式が、次のように得られます。
σθとσθ´より、次のような関係式が得られます。
σθ+σθ´=σx+σy
上の式は、任意の2つの互いに直交する平面上の垂直応力の和が、
一定であることを示しています。
また、
をみると、互いに直交する2つの平面上のせん断応力は、
大きさが等しく符号が反対であることを示しています。
[平面応力]
外力の作用により、弾性体のある断面に垂直応力σx、σy及びせん断応力τが生じるような場合を考えます。
このような状態を平面応力状態にあるといいます。
一軸応力及びニ軸応力は、共に平面応力状態の特別な場合です。
x面、y面に応力が生じれば、z面にもわずかながらポアソン効果により応力が生じます。
しかし、平面応力状態ではz軸の応力成分を0として考えます。
図ではせん断応力τxyは、時計回りの方向に生じると仮定しています。
また、傾斜面上のτθの向きは、σx、σy,τxy(τyx)の大小によって時計回りや反時計回りの方向になりますが、
時計回りの方向に生じると仮定します。
二軸応力と同様、長方形要素から切り取った三角形要素が平衡状態にあることを利用し、
傾斜した面上に生じる応力を求めます。
ここでも二軸応力の場合と同様、せん断力τxy、τθの方向は、はり内部の応力表示法の約束により、
時計回り(正の方向)に仮定しています。
平衡方程式をたてるには、各応力が生じている面積を乗ずる必要があります。
x面の面積をAとすれば、
要素のy面の面積はA・tanθ、傾斜面の面積はA・secθとなります。
先の2つの式を三角関数間の関係式を用いて整理すると、
となります。
これらの式は、任意の傾斜した面上の垂直応力σθ及びせん断応力τθをσx,σyとせん断応力τxyで表したものです。
また、上の式でτxy=0のときは、それぞれニ軸応力状態を表します。
三角形要素を極めて小さいものと仮定すれば、
傾斜面pqは、点rを通るその方向の断面と考えて差し支えありません。
このように考えるとσθ、τθは弾性体内の1点をとおり、
任意の傾きθをなす面上の応力とみなすことができます。
したがって、任意の傾きをなす平面上に生じる応力を決定することができます。
例えば、θ=0のときのせん断応力τθの値は、τxyとなり、
斜面上の向きは時計回りの方向であることを意味します。
x軸とθ+π/2
の角をなす軸に垂直な平面上の応力σθ´ 、τθ´ は、
のσθ式及びτθ式のθに、θ+π/2を代入し求めることができます。
そのときの応力σθ´及びτθ´は、
となり、式σθとσθ´ より、次のような関係式が得られます。
σθ+σθ´=σx+σy
上の式は、任意の2つの互いに直交する平面上の垂直応力の和が、
一定であることを示しています。
また、式τθとτθ´をみると、
互いに直交する2つの平面上のせん断応力は、大きさが等しく符号が反対であることを示しています。
τθ=-τθ´
今一度、任意の傾斜した面上の垂直応力式
において
σθが最大または最小を示す傾斜面の位置を求めます。
σθの極値を求めるためには、上の式をθについて微分し、その微分係数を0とおきます。
となります。また、この式は、
と同じであり、σθが最大または最小をとる場合には、せん断応力が0になることを意味します。
7.1.4 はりの主応力と主応力面
はりは、一軸応力状態、
つまり図においてy軸やz軸方向の垂直応力は存在せず、
x軸方向の垂直応力だけが存在するものとして計算して差し支えありません。
一軸応力状態では、x 軸方向の変形に対して、
ポアソン比に応じて y 軸、z軸方向に自由に変形できる場合には、 y 軸、z 軸方向の応力は生じません。
実際、支点や荷重載荷点近くを除き、この条件が満たされます。
しかし、板のように薄くなると、引張側と圧縮側が近接し、
お互いの影響を受けるため自由には変形ができなくなります。
そのため、x軸方向の垂直応力の他に、y 軸方向の垂直応力が生ずることになります。
弾性体内部の垂直応力σθとせん断応力τθは、傾斜断面の角度θに応じて変化します。
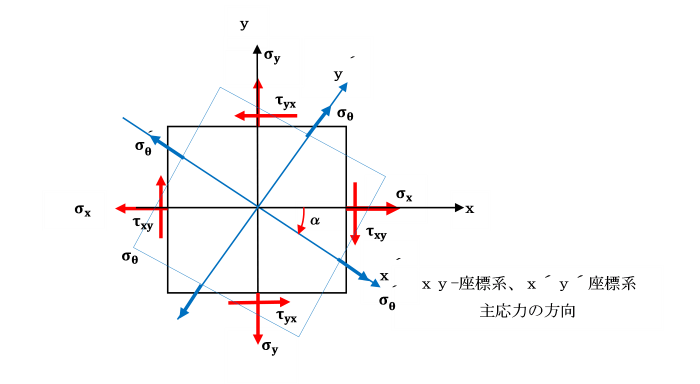
垂直応力の最大値と最小値を主応力といい、
これら2つの垂直応力は、互いに直交する平面上に生じています。
また、これらの断面においては、せん断応力は0となります。主応力が生じる平面を主応力面という。
また、せん断応力が最大、最小となるような面も互いに直交します。
主応力面上の垂直応力とせん断応力が最大、または最小となる面は、互いに45°の角度をなします。
このことは7.1.5 モールの応力円で説明します。
主応力面上おいて、せん断応力0となりますが、
せん断応力が最大、または最小となる面では、垂直応力は必ずしも0になりません。
せん断応力の最大値または最小値を主せん断応力という。
はりの横断面の任意の点における垂直応力とせん断応力を考えます。
垂直応力は、はりの外表面で最大となり、
中立軸では0となります。
また、せん断応力は外表面で0となり、
中立軸において最大値に達します。
はり内部の応力を解析するためには、
これら垂直応力とせん断応力を組み合わせた効果を考える必要があります。
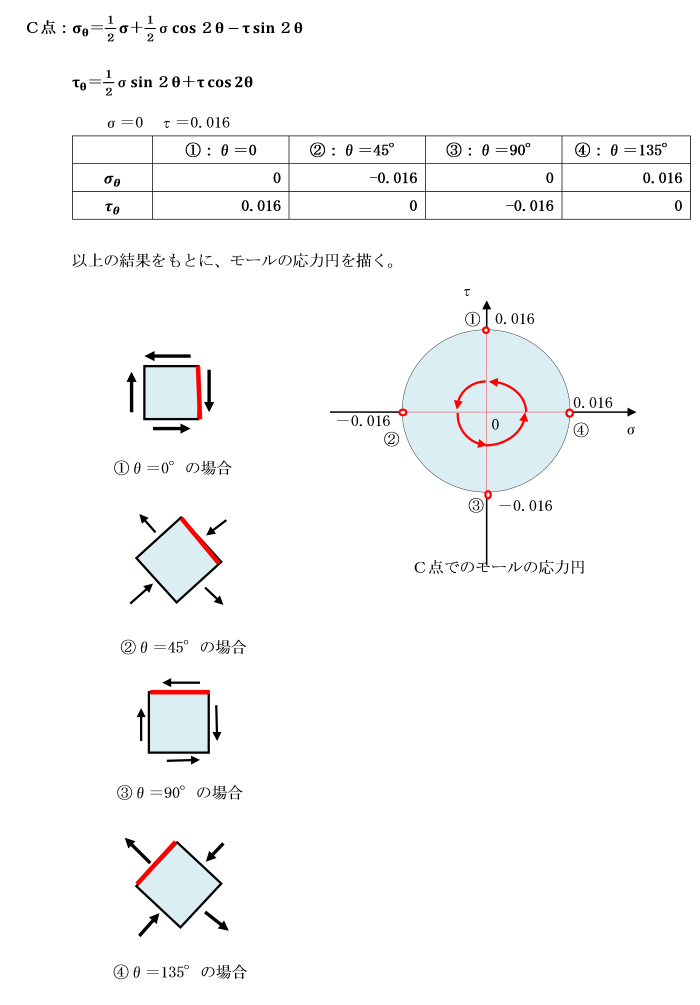
7.1.5 モールの応力円
物体内の応力状態を図示するときに用いられる円であり、
次のように導くことができます。
[一軸応力状態におけるモールの応力円]
棒が単純引張りを受けたときを考えます。
棒の軸線に垂直な面の応力σxと反時計回りに角θをなす傾斜断面上の垂直応力σθとせん断応力τθの関係は、
次のようになります。
棒内の要素を引張る場合を正(+)、時計回りの偶力を正(+)とします。
上の2式は、角2θをパラメータとする方程式であり、
2式の両辺を2乗して加え合わせると、パラメータは消えて、
となり、
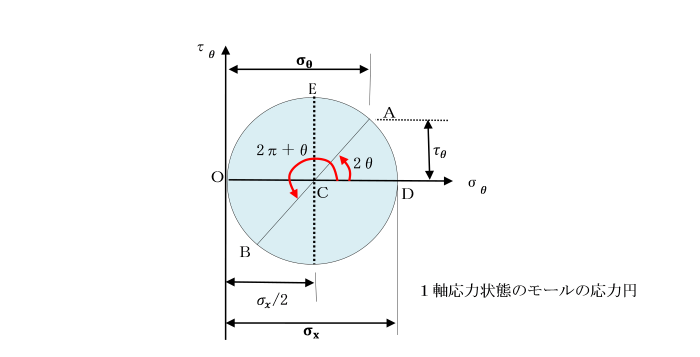
これは、横軸にσθ、縦軸にτθの直交座標軸0-σθ τθにおいて、
中心Cが(σx/2,0)、
半径が(1/2)σxの円の方程式となることが分かります。
この円周上の点が、x軸と反時計回りの傾斜面の角度θにおける垂直応力σθ及びせん断応力τθを表します。
この円をモールの応力円といいます。
モールの応力円において、点Dは、軸に垂直な断面上の応力状態を示しており、
任意の傾斜断面上の応力は点Aで表されます。
点Aは、この円周上をDから反時計方向に回ります。
また、軸線に垂直な面が、反時計回りにθ+π/2の角をなす面上の応力は、
σθ, τθの式θにθ+π/2を代入することによって求められます。
そのときの垂直応力σθ´、せん断応力 τθ´は、
これらσθ´、 τθ´の値は、B点の座標値となります。
棒内の微小要素α、βの応力状態について図示すると次のようになります。
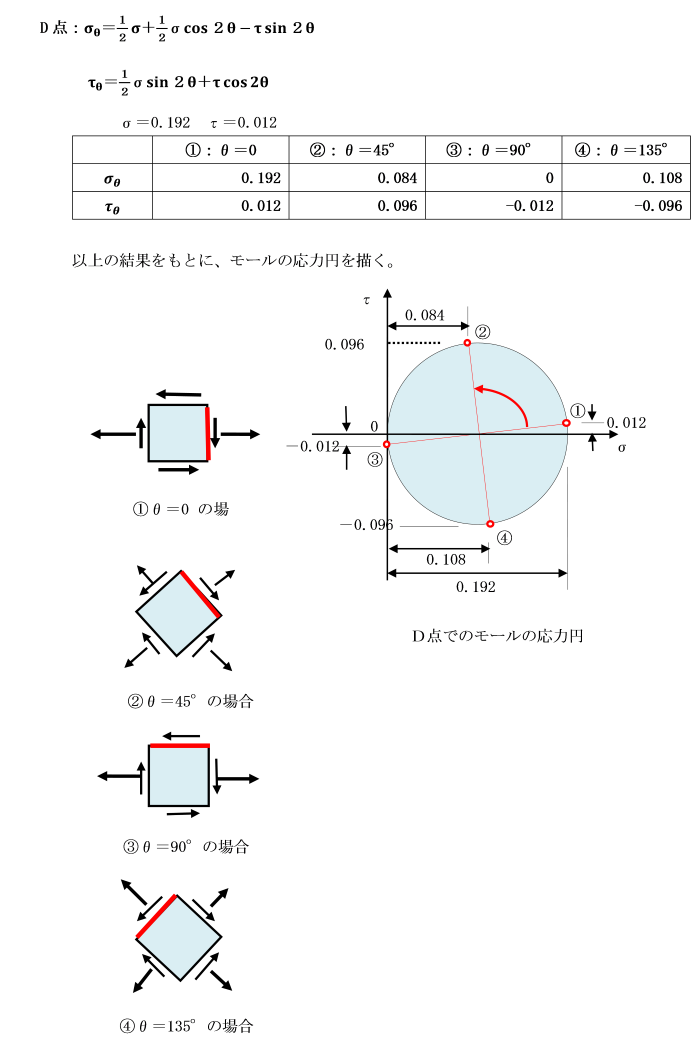
[2軸応力状態におけるモールの応力円]
ある弾性体内の長方形要素を考えます。
垂直応力σx<がx面(x軸に垂直)σyがy面(y軸に垂直)の2方向に生じている状態を考えます。
要素がx軸と反時計回りに角θをなす傾斜した断面上に生じている垂直応力σθ及びせん断応力τθと
σx 、σyの関係は次式のようになります。
ただし、物体内の要素を引張る場合を正(+)、時計回りの偶力を正(+)としています。
垂直応力σθとせん断応力τθは傾斜断面の角度θに応じて変化しますが、
最大あるいは最小になるのはどのような傾斜角度だろうか。
そこで、垂直応力σθとせん断応力τθとの関係を図示してみましょう。
とおくと、次のように書き換えることができます。
上の2式は、角2θをパラメータとする方程式であり、
2式の両辺を2乗して加え合わせると、パラメータは消えて、
となります。
これは、横軸にσθ、縦軸にτθの直交座標軸0-σθ τθにおいて、
中心が(A,0)、半径がBの円の方程式となることが分かります。
A、Bをもとに戻すと、中心が( 1/2・(σx+σy),0)、半径 (1/2)・(σx-σy)の円となります。
この円周上の点が、x軸と反時計回りの傾斜面の角度θの
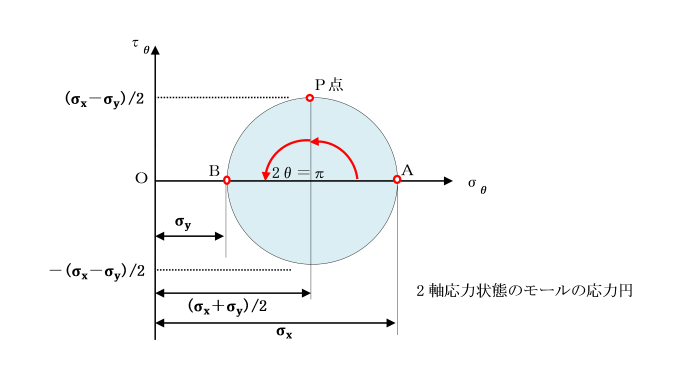
垂直応力σθ及びせん断応力τθを表します。この円をモールの応力円という。
例えば、反時計方向に角θをなす傾斜した断面上を考えます。
そこに生じている垂直応力σθ及びせん断応力τθの式において、
傾斜面の角度θに生じる応力を求めるには、
モールの応力円では反時計回りの方向に2θの角を円周上に求めます。
θ=0からθ=π/2まで反時計回りに回転すると、
垂直応力σθは、σxからσyまで変化します。
垂直応力の最大値と最小値を主応力といい、これら主応力が生じる平面を主応力面という。
主応力面上には、せん断応力は生じません。
せん断応力τθは、θ=0のときは、0で、θ=π/4にとき1/2(σx-σy)となります。
このように垂直応力σx及びσyを用いて、
任意の傾斜した面上の垂直応力及びせん断応力を求めることができます。
モールの応力円は、平面応力を表す一組の値さえあれば、
幾何学的に主応力とその方向が分かります。
σx>σy>0、0≦θ≦π/2 のときは、せん断応力τθの値は正となり、
反時計回りに角θをなす傾斜した断面上には、
時計回りの方向にせん断応力が生じていることを意味しています。
[平面応力状態におけるモールの応力円]
次の式は、ある断面に生じている垂直応力σx、σy及びせん断応力τxy(τyx)が、
反時計回りにθだけ傾斜した断面での垂直応力σθ及びせん断応力τθを表しています。
上の式は、弾性体内の長方形要素に着目し、
長方形要素から切り取った三角形要素の平衡方程式から誘導されたものです。
図ではせん断応力τxyは、時計回りの方向に仮定しています。
また、傾斜面上のτθの向きは、σx、σy,τxy(τyx)の大小によって時計回りや反時計回りの方向になりますが、
時計回りの方向に仮定しています。
つまり、下図のような応力の方向を正としています。
σx、σyが主応力でない状態におけるモールの応力円を求めてみましょう。
平面応力の垂直応力σθとせん断応力τθは、傾斜断面の角度θに応じて変化します。
最大あるいは最小になるのはどのような傾斜角度だろうか。
2軸応力の場合と同様に垂直応力σθとせん断応力τθとの関係を図示してみます。
図示するために、
とおくと、次のように書き換えることができます。
上の2式は、角2θをパラメータとする方程式であり、
2式の両辺を2乗して加え合わせると、パラメータは消えて、
このように垂直応力σx 及びσyを用いて、
任意の傾斜した面上の垂直応力及びせん断応力を求めることができます。
もう一度、平面応力状態での垂直応力σθ及びせん断応力τθの式を調べてみましょう。
垂直応力の最大値と最小値を主応力といい、
これら主応力が生じる平面を主応力面という。
主応力面上には、せん断応力は生じない。
σθ軸上の交点P、Qは、せん断応力τが0であるから、主応力となります。
傾斜断面に生じる応力のつり合い式を求めるときに、
x面から反時計回りに角θをとっています。
モールの応力円の角2θも同様に、反時計回りとなります。
これは、弾性体内の切り取った三角形要素の応力の方向を図のように設定しているためです。
また、角2θは三角形要素の平衡状態に対するσθ及びτθの2つの方程式を誘導する過程で、
実際の作用面での角度θ が計算上は2θ になっていることに起因しています。
点A(σx,τxy)から時計回りに2αだけ傾斜すると、
(σ1,0)の点になることは、
最初に設定したxy軸から時計回りにαだけ回転したx´ y´軸では垂直応力のみが生じ、
せん断応力が0になることを意味しています。
そのため、モールの応力円においては、
tan2α=2τxy/(σx-σy) を満足する角2αの面が主応力面となります。
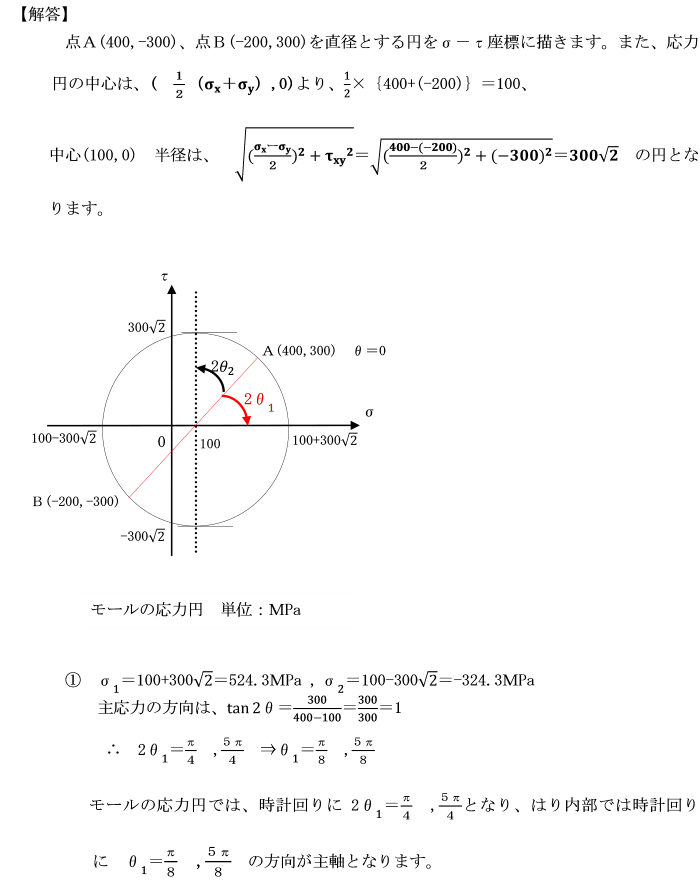
【例題7-1】
σx=400MPa, σy=-200MPa, τxy=300MPaであるとき、
① 主応力とその主軸の方向を求めなさい。
② σxが生じる面から最大せん断応力とその方向を求めなさい。
③ σxが生じる面から反時計回りに30°回転した面の応力状態を示しなさい。
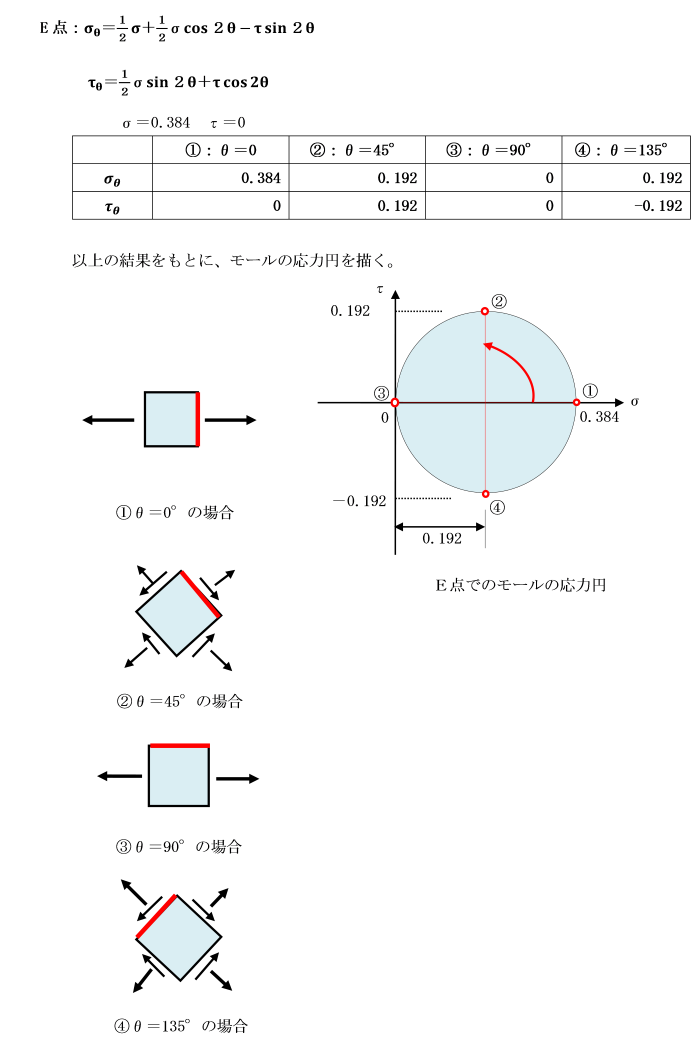
7.1.6 はり内部の応力状態
主応力の大きさと方向が、
長方形断面のはりの内部でどのように変化するかを調べてみましょう。
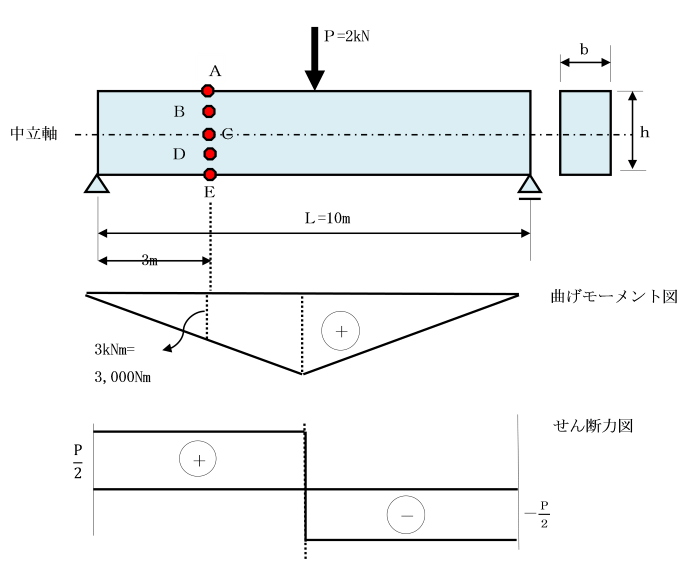
今、次のような諸元をもつ長方形断面の単純ばりを考えます。
はりの中央に集中荷重Pを作用させます。
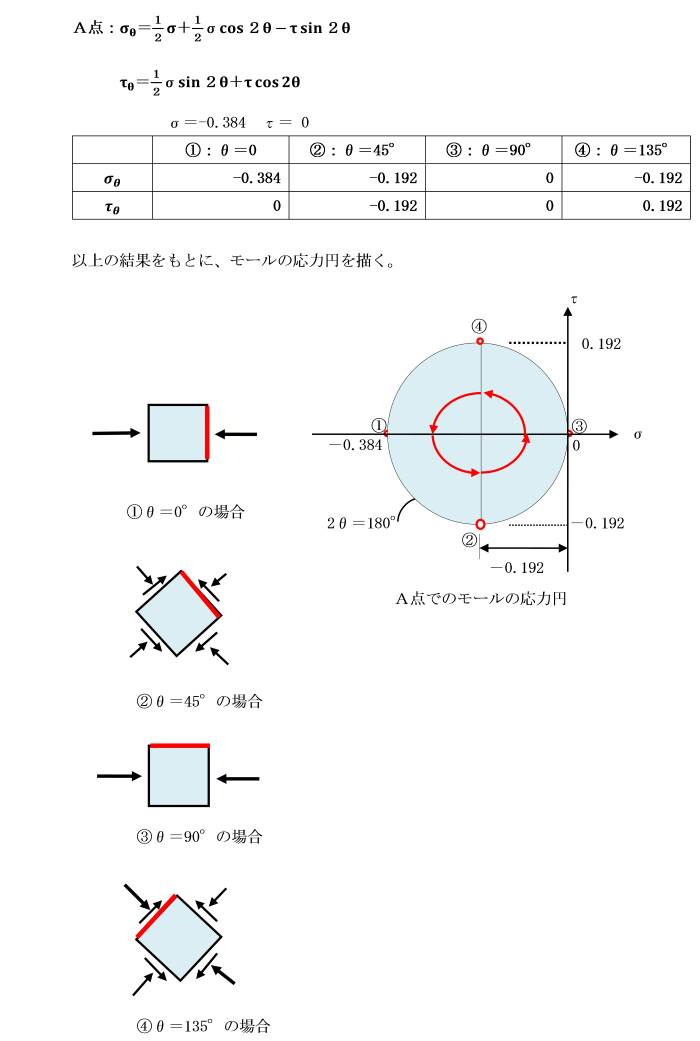
図のA,B,C,D及びE点を断面上に選定します。
点AとEは、それぞれはりの上側と下側の表面、
点Cは、はりの中立軸上の点、点BとCは外表面と中立軸との中点とします。
7.2 はりの支点反力・断面力の影響線
7.2.1 影響線
自動車、歩行者のような荷重は、はりの軸方向に移動します。
このような移動する荷重を移動荷重という。
特に、荷重と荷重の間隔を一定に保持する移動荷重を連行荷重という。
移動荷重や連行荷重が、はりのいかなる位置に作用しても構造物が安全であるように、
その部材の断面寸法を決定することは、極めて重要なことです。
そのためには、着目する断面に最大断面力を生じさせるような荷重の位置はどこか、
また、このような荷重の配置のもとで、その断面の応力、たわみを求める必要があります。
移動荷重により構造物に生ずる最大断面力あるいは最大反力などを計算するには、影響線を利用すると便利です。
影響線とは、単位の移動荷重によって、はりの任意断面に生じる反力、断面力、たわみなどの量が、
どのように変化するかを、荷重の作用点からの縦距で表示したものです。
7.2.2 はりの影響線
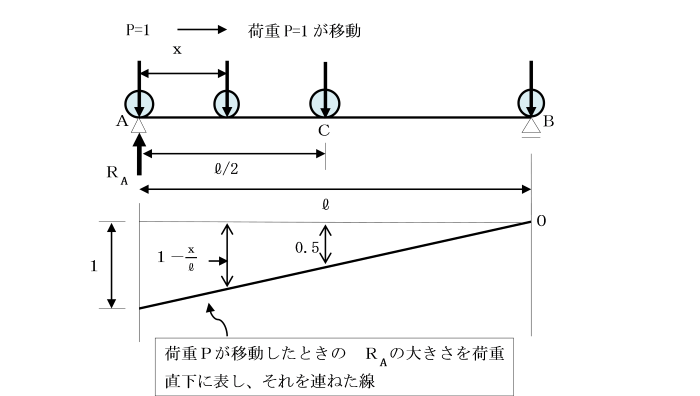
【単純ばり】
反力の影響線
反力RAは、P=1がA点にきたときには、RA=1、
C点(中央点)にきたときには、RA=0.5、
B点にきたときには、RA=0となります。
これらの点を連ねた線は、直線となり、これを支点反力RAの影響線という。
今、単位荷重P=1が、左支点からxのところにあるとします。
このとき反力RAは、点Bをモーメントの中心とすると、
ΣMB=0より、
RAl-1・(l-x)=0 ∴ RA=1-x/l となります。
荷重位置によるRAの大きさは、荷重直下の縦距yで表されます。
同様にRBの影響線については、下図のようになります。
単位荷重P=1が左支点からxのところにあるとすると、
反力RBは、点Aをモーメントの中心とすると、
ΣMA=0より、
-RBl+1・x=0 ∴ RB=x/l となります。
荷重位置によるRBの大きさは、荷重直下の縦距yで表されます。
この影響線を応用する例として、
列車荷重のような連行荷重が、移動する場合の反力を調べてみましょう。
下図のような連行荷重P1,P2,P3が作用する場合、
はりABの左支点の反力RAの値は、次のようにして求められます。
P1,P2,P3の荷重位置から鉛直線を下し、
各荷重に対する縦距y1,y2, y3を求めると、
RA= P1・y1+P2・y2,+P3・y3
連行荷重P1,P2,P3が、作用した場合の反力RAを求めることができます。
なぜならば、y1,y2, y3は、
単位荷重1に対するA点での反力です。
したがって、P1による影響はP1・y1、P2,P3による影響は、
それぞれとP2・y2,,P3・y3となり、
同時に作用しているからこれらを重ね合わせればよい。
せん断力の影響線
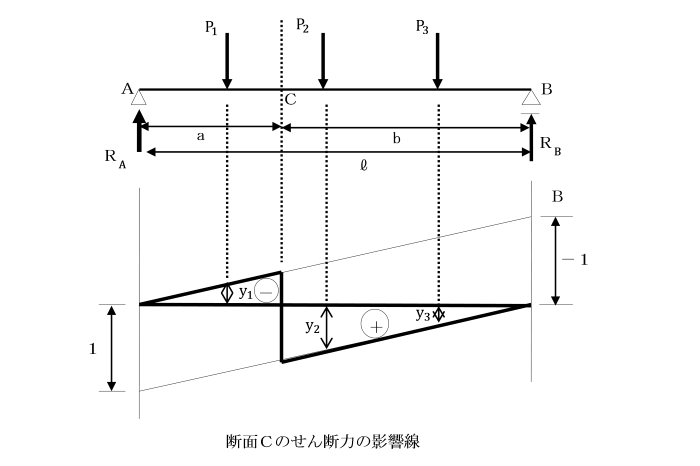
支点Aから距離aにある断面Cのせん断力の影響線を求めましょう。
移動荷重P=1が断面Cの左の部分、AC間(0≦x≦a)に作用している場合のせん断力Scは、
Sc=RA-P=-RB=-x/l となります。
また、荷重P=1が断面Cの右の部分、CB間(a≦x≦l)に作用している場合のせん断力Scは、
Sc=RA=1-x/l となります。
この影響線を応用する例として、
連行荷重P1,P2,P3がはりABに作用する場合のC点のせん断力を求めます。
各荷重P1,P2,P3の位置から鉛直線を下して、
それが影響線を切る各々の長さをy1,y2, y3とすると、C点のせん断力Scは、
Sc=P1・y1+P2・y2,+P3・y3 となります。
この式のy1は(-)になることに注意する必要があります。
曲げモーメントの影響線
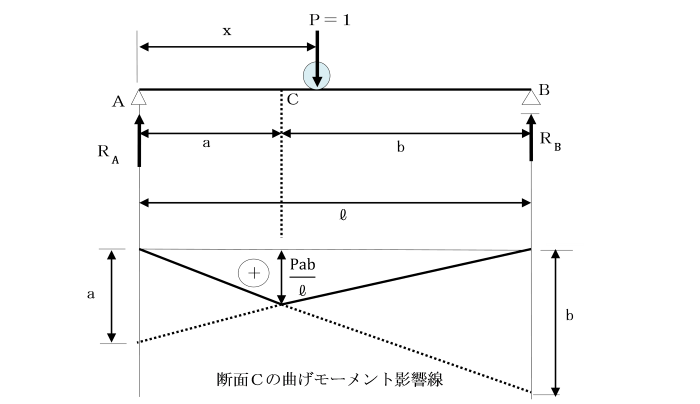
支点Aから距離aにある断面Cの曲げモーメントの影響線を求めましょう。
移動荷重P=1の作用位置を支点Aから距離xで表します。
荷重Pが断面Cよりの左の部分、AC間(0≦x≦a)に作用している場合、
曲げモーメントMcは、断面Cより右側のつりあい条件式より、
Mc=RB・b=1・(x/l)・b=b(x/l) (0≦x≦a) です。
また、荷重Pが断面Cより右の部分、CB間(a≦x≦l)に作用する場合、
Mcは、断面Cより左側の力のつり合い条件式から、
Mc=RA・a={(1-x)/l}a=a(1-x/l) (a≦x≦l) です。
これらの式からMcの影響線は、
RAとRBの影響線1-x/l及びx/lをそれぞれa、b倍して求められます。
荷重Pがはりを移動する場合、
断面Cの曲げモーメントは、Pが断面Cに作用した場合が最大で、その値はPab/lとなります。
【片持ちばり】
せん断力の影響線
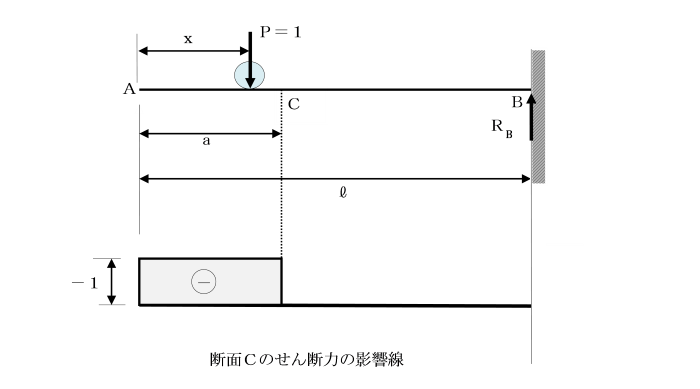
断面Cに生じるせん断力の影響線を求めましょう。
荷重P=1が断面Cより左の部分(0≦x≦a)に作用する場合は、
Sc=-1であり、また、P=1が断面の右の部分(a≦x≦l)に作用する場合は、
Sc=0です。
曲げモーメントの影響線
断面Cに生じる曲げモーメントの影響線を求めましょう。
荷重P=1が断面Cより左の部分(0≦x≦a)に作用する場合、Mcは、
Mc=-1・(a―x) となります。
また、P=1が断面の右の部分(a≦x≦l)に作用する場合は、Mc=0です。
間接荷重の場合
[支点反力の影響線]
支点反力は、荷重とのつり合い条件によって決まり、
荷重の伝達方法には無関係に求めることができます。
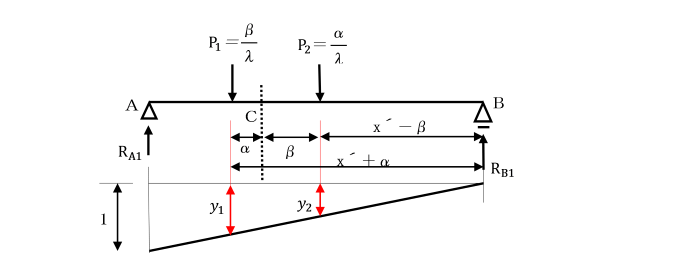
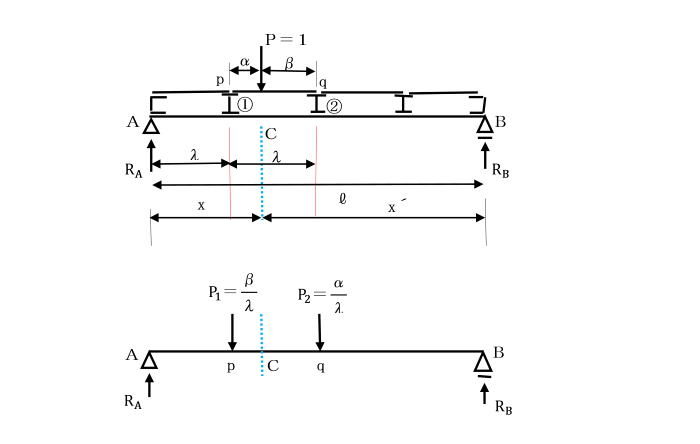
図のような間接荷重を受ける単純ばりを考えます。
荷重P=1は、横げた①②をとおして、P1とP2分かれ、はりABに伝達されます。
このときのA点の支点反力RAの影響線は、
下図のようになり、反力の大きさは、
RA1=P1・y1+P2・y2 となります。
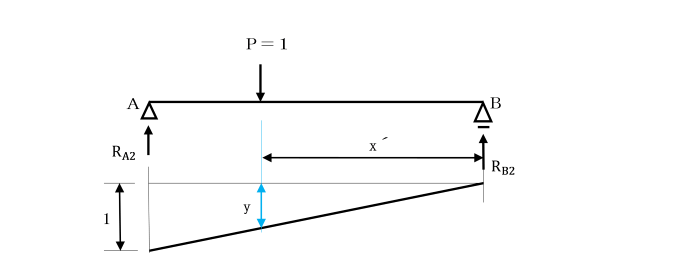
一方、荷重P=1がはりABに直接作用する場合は、
図のようになり、そのときのA点の支点反力RA2の影響線は、
RA2=P・y となります。
RA1=P1・y1+P2・y2 と RA2=P・y が等しければ、
支点反力の影響線は、間接荷重と直接荷重の区別は必要なく、
間接荷重の場合にも直接荷重の影響線を用いることができます。
[せん断力の影響線]
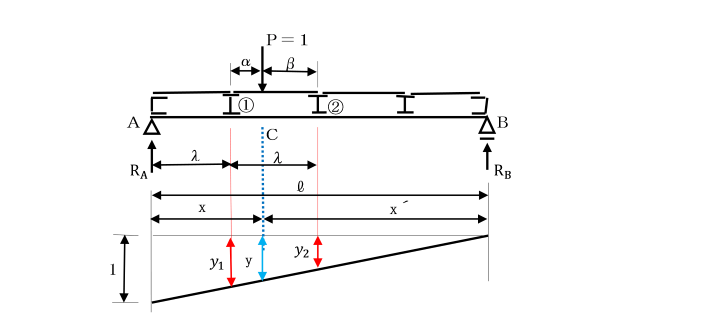
間接荷重が作用しているときの断面Cのせん断力の影響線を求めましょう。
荷重P=1が横げた①②の間に作用したときには、
荷重P=1はpqを単純ばりと考えれば、
横げた①②をとおしてP1とP2に分かれ、単純ばりABに伝達されます。
したがって、P1=β/λ、P2=α/λ となり、
支点反力RAは、(l-λ-α)/l となります。
荷重P=1がpq間に作用した場合のこの区間のせん断力Sxは、
Sx=RA-P1
=(l-λ-α)/l-β/λ となり、
αまたはβの1次式で与えられ直線となります。
荷重Pがpq以外の部分に作用した場合は、
C点のせん断力は、荷重が直接作用したときと全く同じになります。
なぜならば、断面pの左側またはqの右側に荷重が間接あるいは直接作用しても
支点反力の値は同じになるからです。
図は間接荷重が作用しているときの断面Cのせん断力の影響線です。
[曲げモーメントの影響線]
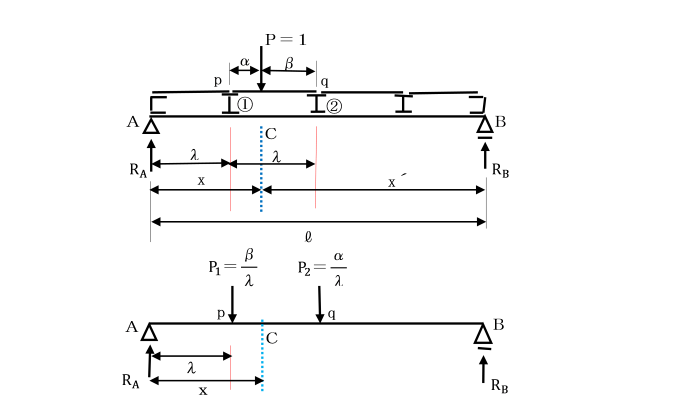
間接荷重が作用しているときの断面Cの曲げモーメントの影響線を求めましょう。
P1、P2の大きさは、pqなる単純ばりの反力として求めればいいことから、
P1=β/λ、P2=α/λ となり、支点反力RAは、(l-λ-α)/l となります。
荷重P=1がpq間に作用した場合、
この区間の曲げモーメントMxは、
Mx=RA・x-P1(x-λ)
=(l-λ-α)/l x-β/λ(x-λ) となり、
αまたはβの1次式で与えられ直線となります。
したがって、断面Cを含んだ間接荷重の区間(pq)は、
直接荷重を受ける場合の影響線において、その区間(pq)を直線で結べばよい。
図は間接荷重が作用しているときのC点の曲げモーメントの影響線です。
7.2.3 相反作用の定理
弾性線形構造物に2組の互いに独立な外力群1及び外力群2が作用して、
それぞれの系でつり合状態にあるとき、
外力群1が外力群2により生ずる変位に対してなす仮想仕事は、
外力群2が外力群1により生ずる変位に対してなす仮想仕事に等しい。
ベッティの「相反作用の定理」と呼ばれるものです。
重ね合わせの原理より、
荷重の載荷する順序によらず
弾性線形構造物の内部に蓄えられるひずみエネルギーが、
同じであることを利用して求められる定理です。
相反作用の定理を理解するために、
まず、外力による仕事と内力による仕事について考えましょう。
(1)仕事とその性質
構造解析では、仕事という概念は重要な役割をはたします。
構造物に外力が作用すれば、
外力の作用点は変位するから、外力は仕事をします。
これを、外力による仕事といいます。
一方、外力が作用すると、
変位に起因して部材内部には変形が生じ、
同時に構造物内部には応力が生じます。
構造物内部で応力が変形に対して行う仕事を、
内力による仕事といいます。
内力による仕事は、
ひずみエネルギーとして構造物内に蓄積されます。
ひずみエネルギーは、
仕事をする潜在的な能力を持っているため、
ポテンシャルエネルギーとも呼ばれます。
構造物は弾性的にふるまうため、
外力を作用するときと除去するときの間で、
エネルギーの損失はないものと考えます。
外力による仕事と内力による仕事の大きさは等しい。
これはエネルギー保存の法則と呼ばれます。
弾性体内で、応力-ひずみの関係が
σ=E・εのように線形になっているものを、
線形弾性体といいます。
また、ゴムなどの高分子材料は、
応力-ひずみの関係が非線形ですが、
応力とひずみの関係は1対1対応です。
このようなものを非線形弾性体といいます。
(2)外力の仕事
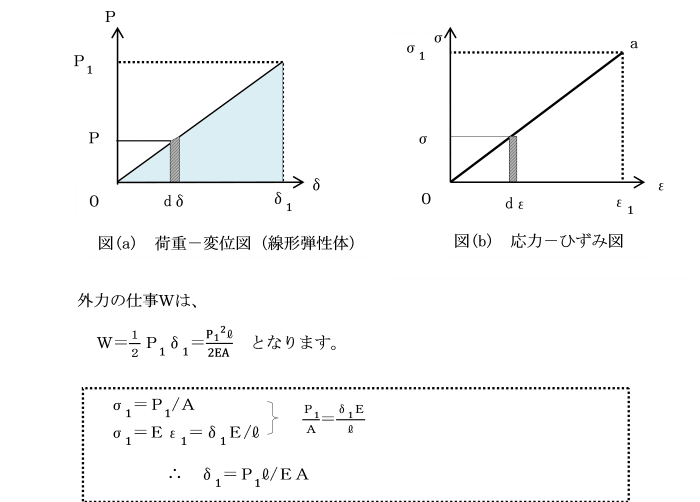
図のように荷重P-変位δの関係(a)にある非線形弾性体の構造物を考えます。
変位が0からδ1に変化する途中に微小な変位dδをとり、
荷重Pが作用すると、荷重Pによる仕事dWは、
dW=P・dδ
となります。
dδは荷重Pが作用している方向に生じているとします。
すると、変位が0からδ1まで増加する間に荷重Pが行う仕事は、
となり、
これは、荷重Pが変位δの関数として変化する場合の外力による仕事で、
荷重-変位図の下方にある面積に相当します。
もし構造物が図(b)に示す線形弾性体で、
変位δに比例して荷重Pが作用する場合には、
外力の仕事Wは、W=1/2 P1・δ1となります。
ここで注意すべきことは、
右辺に1/2という係数がついていることです。
これは、弾性体に荷重を作用させて変形させる際に、
物体に振動を与えないように、荷重を0から徐々に加え始め、
最終値にまで増大しているからです。
荷重―変位図の下方にある面積に相当します。
(3)内力の仕事
物体が仕事を行う能力を有するとき、
その物体は、エネルギーを有します。
ひずみが生じた物体が有するエネルギーのことをひずみエネルギーといいます。
ひずみエネルギーの大きさは、
ひずみが生じた物体が元の状態、
つまり、無ひずみ状態に復帰するまでに行う仕事量によって表されます。
内力の仕事は、ひずみエネルギーとして構造物に蓄えられます。
代表的な変形に対して、
外力の仕事と内力による仕事(ひずみエネルギー)を求めてみましょう。
A.引張を受ける棒の外力仕事と内力仕事
[外力による仕事]
今、引張力を受ける棒を考えます。
棒は、外力Pにより応力σ=P/Aを生じます。
また、棒は、線形弾性体で、フックの法則にしたがう場合を考えます。
棒のひずみε=δ/lであり、
外力Pとそれによる変位δの間には、
図(a)のような関係があります。
また、棒部材の断面に生じる応力σとひずみεとの間には、
図(b)のような関係があります。
[内力(ひずみエネルギー)による仕事]
棒内のある任意の微小要素に着目すると、
荷重Pが0から徐々に増加して最終値P1に達したときの
応力及びひずみをσ1、ε1とします。
材料の単位体積のひずみエネルギーU0は、
ここにε1は、ひずみの最大値で
ε1=δ1/l。
U0は、応力-ひずみ図の下にある部分の面積を示しています。
全体のひずみエネルギーUは、
棒の断面積をA、長さをlとすると、
単位体積のひずみエネルギーを
全体積(V=Al)にわたって行うことにより求めることができます。
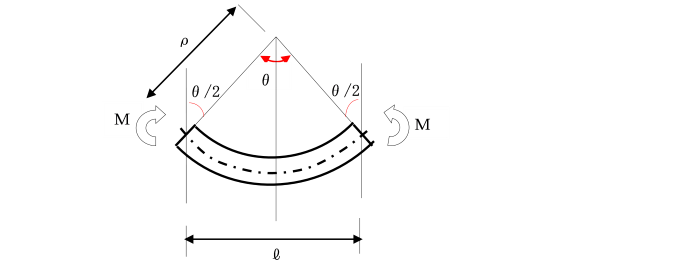
B.モーメント荷重を受けるはりの外力仕事と内力仕事
[外力による仕事]
図に示すように、
両端にモーメント荷重Mを受けて
曲げ変形をするときの外力による仕事を求めます。
モーメント荷重Mによるはりの変形量は、
回転角θで表され、
Mとθの関係は、
荷重-変位図に示すように直線0aで表されます。
回転角が0からθ1に変化する途中に
微小な回転角dθをとり、
モーメント荷重Mが作用すると、
モーメント荷重Mによる仕事は、
斜線部分の長方形の面積 M・dθ となります。
このことから、モーメント荷重Mの外力による仕事Wは、
ここで、はりの長さをl、
曲げ剛性をEIとすると、
モーメント荷重Mと回転角θとの間には、
θ=Ml/EIの関係※1があるから、
内力(ひずみエネルギー)による仕事
微小要素の体積をdV(=dxdydz=dAdx)とすれば、
微小要素内に蓄えられるひずみエネルギーdUは、
dU=1/2σεdV となります。
この式そのものが
既にモーメント荷重Mが0から
徐々に増加して最終値M1に至るまでの
微小要素内に蓄えられるひずみエネルギーです。
モーメント荷重を受けるはりの微小要素のyz面に生じる応力は、
y軸の位置によって変化するため、
σ及びεには以下の式を代入する必要があります。
σ=M1/I y
ε=σ/E=M1 y/EI
dU=(M12/2EI2 ) y2dAdx となります。
C.せん断力が作用する弾性体の外力仕事と内力仕事
[外力による仕事]
図に示すように
直方体にせん断力Sが作用して破線のような形に変形し、
せん断ひずみγが生じたときに、
せん断力Sの外力仕事Wは、
W=1/2S・⊿=(S2h)/2GA となります。
⊿=γh=Sh/GA
※ S/A=(G⊿)/h
⊿はせん断力Sの作用により生じたずれを表す。
Gはせん断弾性係数
(τ=S/A τ:せん断応力、S:せん断力、A:横断面の面積)
内力(ひずみエネルギー)による仕事
せん断変形を受ける弾性体では、
τ=S/A、γ=S/GAと表されます。
また、図より、⊿=γhであるから、
ひずみエネルギーUは、
U=(1/2)τγV
U=(1/2)×(S/A)×(S/GA)×Ah=S2h/2GA
したがって、外力がなす仕事と内力の仕事は等しいから、
W=Uが成立します。
次に別種の仕事、いわゆる補助仕事W※について考えます。
これは、後に説明するカスティリアノの第2定理を導く際に必要となり、次式で定義される。
補助仕事は、荷重-変位図の縦軸との間の面積で表されます。これは、仕事Wのように物理的な意味は持っていない。
W+W※=P1δ1 の関係にあります。
補助エネルギーU※は補助仕事W※に等しい。したがって、
材料の単位体積についての補助エネルギーu※を考えます。応力σ及びひずみεが生じており、単位体積のひずみエネルギーを定義したように、
応力-ひずみ図が線形関係にある場合は、補助エネルギーとひずみエネルギーは等しくなります。しかし、これら2つのエネルギー量はまったく別種のものです。
[変位の相反作用の定理]
相反作用の定理を説明するための例として、単純ばりで考えましょう。
はりの材料が、線形弾性的で、たわみが小さければ、はりのたわみを求めるのに重ね合わせの原理が適用できます。
両荷重によるはりのひずみエネルギーは、2つの荷重が加えられる順序に影響されません。
つまり、はりに両荷重が同時に加えられても、あるいは一方の荷重が先に加えられ、
次に他方の荷重が加えられてもひずみエネルギーは同じです。
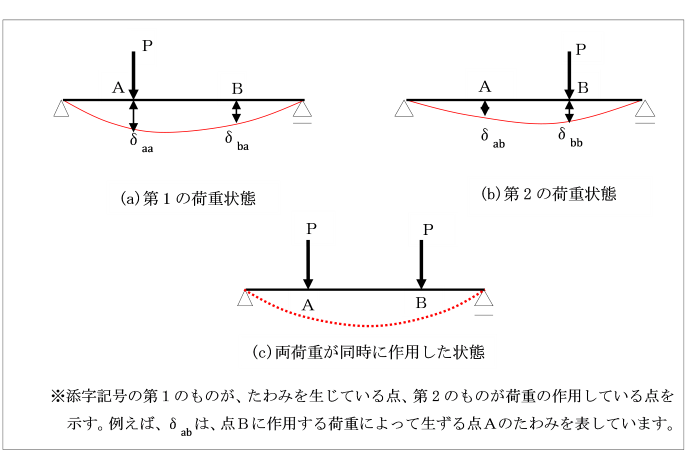
【第1パターン】
・(C)図のように点A、Bに荷重Pが作用している場合を考えます。
Aに対応するたわみは、δaa+δabで、
Bに対応するたわみは、
δba+δbbです。
今、はりに両荷重が徐々に、そして同時に加えられたとき、
荷重によってなされる外力仕事Wは、
はりの内力による仕事、
いわゆる全ひずみエネルギーUに等しく、
W=(1/2)P(δaa+δab)+(1/2)P(δba+δbb)=U となります。
【第2パターン】
・(a)図のように先に点Aに荷重を0から徐々に加え、
次に(b)図のように点Bに荷重が加えられた場合を考えます。
まず、点Aに荷重を0から徐々に加え始め、最終値Pにまで増大させると、
はりのひずみエネルギーU1は、
外力仕事W1と等しいことから、
U1=W1=(1/2)Pδaa となります。
第1の荷重状態に至ってから、
次に点Bに荷重を0から加え始め、最終値Pにまで増大させると、
点Bではδbbだけの追加のたわみが生じます。
点Bに作用した荷重によって、はりのひずみエネルギーU2は、
外力仕事W2と等しいことから、
U2=W2=1/2Pδbbとなります。
しかし、点Bに荷重が加えられている間に、
すでに点Aに作用していた荷重は最終値Pに至っており、
点Aにおいて追加的なたわみδabが生じています。
つまり、点Aでの追加の仕事量は、
U3=Pδabとなります。
ここで係数1/2がないのは、
点Bに荷重が作用する前に、すでに点Aにおいて作用していた荷重は、
最終値Pに至っているからです。
したがって、全ひずみエネルギーUは、
U=U1+U2+U3
=(1/2)Pδaa+(1/2)Pδbb+Pδab となります。
このひずみエネルギーの量は、
2つの荷重が同時に加えられたときに生ずるひずみエネルギーに等しくなります。
【第1パターン】 =【第2パターン】
(1/2)P(δaa+δab)+(1/2)P(δba+δbb)=(1/2)Pδaa+(1/2)Pδbb+Pδab
整理すると、次の結果を得ます。
δab=δba を変位の相反定理といいます。
点Bに作用する荷重による点Aのたわみは、点Aに作用する同じ荷重による点Bのたわみに等しい。
また、変位の相反定理は、
①1つの荷重が力で、他方がモーメント荷重
②両方がモーメント荷重
の場合においても適用できます。
①1つの荷重が力で、他方がモーメント荷重の場合
第1のはりにモーメント荷重Mが作用した場合の変位は回転角θaaで、
第2のはりについてはθabです。
荷重モーメントM及びPが同時に加えられたときのひずみエネルギーU1は、
U1=(1/2)M(θaa+θab)+(1/2)P(δba+δbb) となります。
次にモーメント荷重Mが先に加えられ、
最終値Mに至った後、
荷重Pが加えられた場合のひずみエネルギーU2は、
U2=1/2Mθaa+(1/2)Pδbb+Mθab となります。
これらのひずみエネルギー式U1、U2は等しいことから、
Mθab =Pδba となります。
MとPの数値が等しければ、
θab =δba が成立します。
【例題7-2】
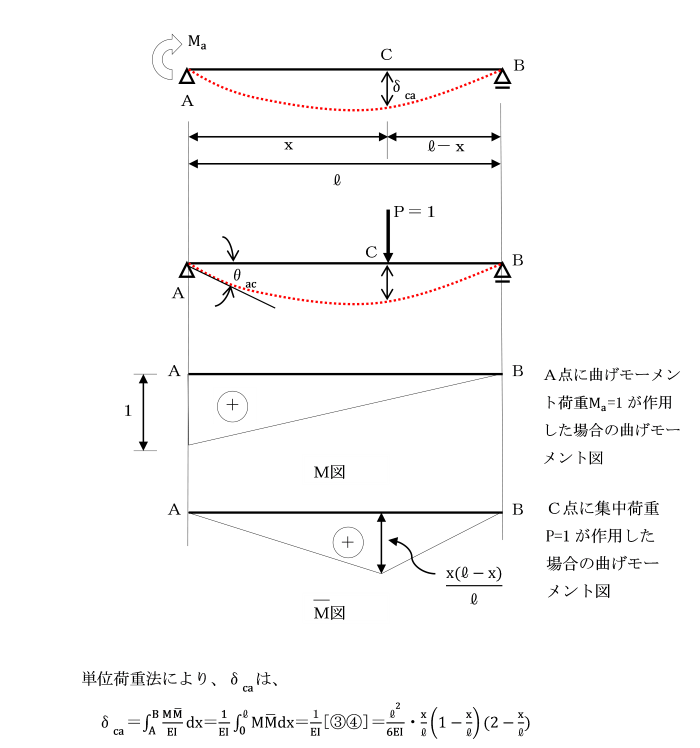
図の単純ばりの支点Aにモーメント荷重Ma=1が作用するときの断面Cのたわみδcaは、断面Cに単位集中荷重P=1が作用するときの支点Aのたわみ角θacに等しいことを示せ。ただし、曲げ剛性(EI)は、はり全体にわたり一様です。
[仕事の相反作用の定理]
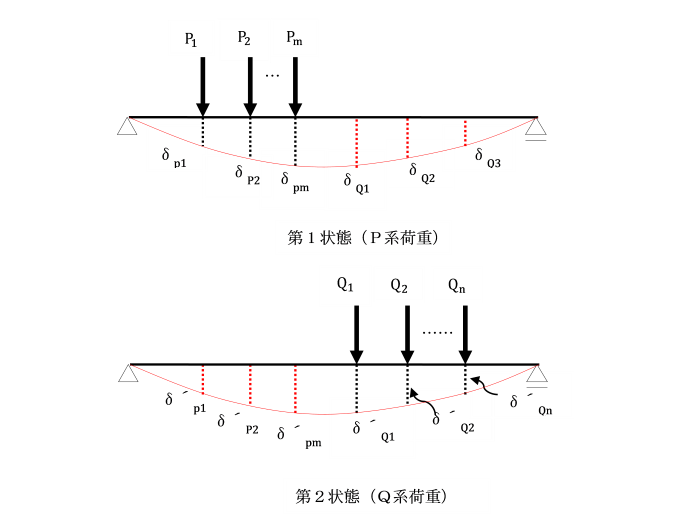
単純ばりに作用する2つの系の荷重状態を考えます。
第1状態においては、m個の荷重群P1, P2, P3,…, Pmが作用し、
第2状態においてはn個の荷重群Q1, Q2,Q3,…Qnが作用しています。
両荷重によるはりの全ひずみエネルギーは、
2つの荷重が加えられる順序に影響されません。
両荷重系(第1状態及び第2状態)のP系及びQ系荷重が、
はりに同時に加えられたとき、
外部仕事WPQは、全ひずみエネルギーUPQに等しいことから、
WPQ=(1/2)P1(δp1+δ´p1)+(1/2) P2(δp2+δ´p2)+……+(1/2) Pm(δpm+δ´pm)
+(1/2)Q1(δQ1+δ´Q1)+(1/2)Q2(δQ2+δ´Q2)+……+(1/2)Qn(δQn+δ´Qn)=UPQ
となります。
このひずみエネルギーは、
はじめにP系の荷重を作用させた後に、
Q系の荷重を作用させたときの全ひずみエネルギーに等しくなります。
P系の荷重が作用したときのひずみエネルギーUPは、
UP=(1/2)P1δp1+(1/2)P2δp2+……+(1/2)Pmδpm となります。
次に、Q系荷重が作用したときのひずみエネルギーUQは、
UQ=(1/2) Q1δQ1+(1/2) Q2δQ2+……+(1/2)QnδQn となります。
さらに、P系荷重が作用した後に、
Q系荷重が作用することにより、
P系荷重は次のひずみエネルギーが加わります。
UP´=P1 δ´p1+P2δ´p2+……+Pmδ´pm
したがって、
UPQ=UP+UQ+UP´
整理すると、
(1/2)(P1δ´p1+P2δ´p2+……+Pmδ´pm)=(1/2)(Q1δQ1+Q2δQ2+……+QnδQn)
この方程式の左辺の式は、
P系の力とそれらに対応するQ系の力によって引き起こされる変位との積の和を表しています。
また、右辺の式は、
Q系の力とそれに対応するP系の力によって引き起こされる変位との積の和を表しています。
第1状態(P系荷重)の力が、それらに対応する第2状態(Q系荷重)の力による変位に対する仕事は、
第2状態の力がそれらに対応する第1状態の力による変位に対する仕事に等しい。
ただし、この定理は、重ね合わせの原理が適用できる構造物に対して有効です。
変位の相反作用の定理は、
仕事の相反作用の定理の特別な場合であることは理解できます。
つまり、仕事の相反作用の定理を
2つの荷重状態の場合に適用すれば、
Pδab=Pδba ⇒ δab=δba を得ます。
この式は、構造力学において有用な原理となっています。
この原理を用いて、構造物の変形(たわみ、たわみ角)の影響線を
直ちに求めることができます。
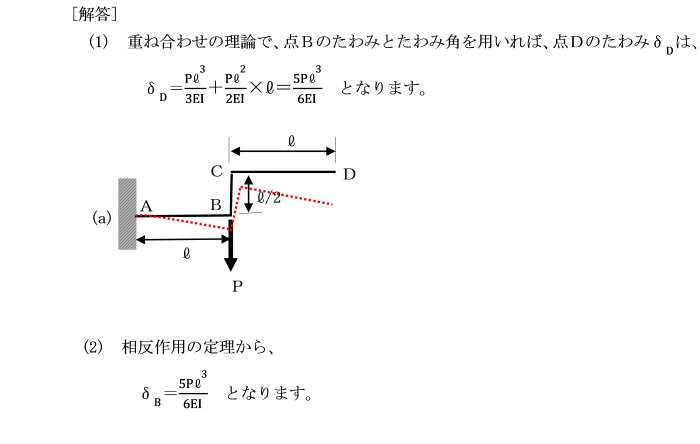
【例題7-3】
図のような、3本の 直線部材からなる左端が埋め込まれた構造を考えます。
曲げ剛性はEIです。
(1) 図(a)の点Bに荷重Fを載荷させたときの、点Dのたわみを求めよ。
なお、点Bのたわみ、たわみ角はそれぞれPl3/3EI、Pl2/2EIです。
(2) 図(b)の点Dに荷重Pを載荷させたときの、点Bのたわみを求めよ。
7.2.4 ミューラ・ブレスロウの原理
構造物の任意の点iにおける力(断面力、反力)の影響線は、
その力だけが作用できない仮想的な構造物を考えます。
そしてその力の方向に単位の変位が生ずるような力を作用させます。
そのときのたわみ曲線の符号を変えたものに等しい。
べッティの相反作用の定理を利用して、はりの影響線を描く手法です。
べッティの相反作用の定理
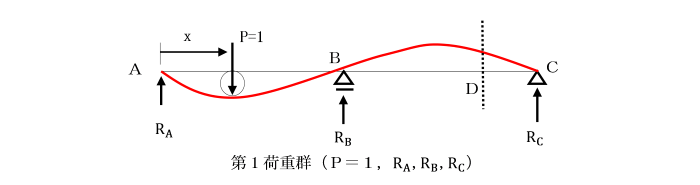
図に示す2径間連続ばりの
支点反力RA及び任意点Dの曲げモーメントMD、せん断力SDの影響線を求めましょう。
図の実線(赤)は、単位の移動荷重P=1が、
支点Aから移動してxの位置にあるときのたわみ曲線を示しています。
(1)RAの影響線
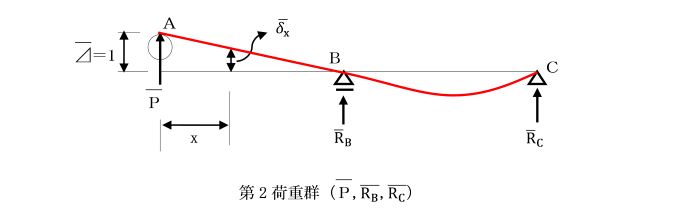
支点反力RAが生じないように支点Aを取り除きます。
元の構造物に移動荷重P=1によって生じるA点の反力RAを作用させれば、
元の2径間連続ばりと力学的に同じたわみ曲線が得られます。
このときの荷重と支点反力(P=1,RA, RB, RC)を第1荷重群とします。
次に、仮想的な構造物のA点に、支点反力RAの方向に単位の変位⊿=1を与える。
このために必要な大きさの荷重Pを作用させたときのたわみ曲線を考えます。
このときの荷重と支点反力(P,RB,RC)を第2荷重群とする。
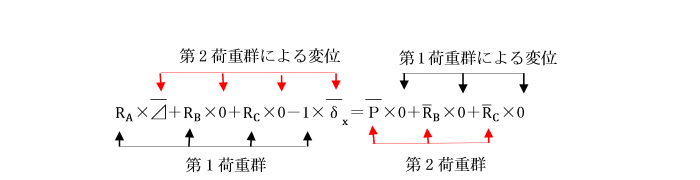
第1荷重群と第2荷重群に対してべッティの定理を適用すると、
(2)MDの影響線
曲げモーメントMDが生じないようにD点をヒンジにします。
ヒンジを入れない元の構造物に、
単位の移動荷重P=1によって生じる曲げモーメントMDを、ヒンジ点Dに作用させれば、
元の2径間連続ばりと力学的に同じたわみ曲線が得られます。
つまり、ヒンジ端に上側引張になるような一対のモーメント荷重MDを与えます。
このときの荷重と支点反力(RA, RB, RC,P=1,MD)を第1荷重群とします。
図は、ヒンジ点Dにモーメント荷重MDの方向に
相対たわみ角の和が1(θ=θ1+θ2=1)となるような変形を与えるモーメント荷重Mを作用させます。
そのときのたわみ曲線を示しています。
このときの荷重と支点反力(RA,RB,RC,M)を第2荷重群とします。
(3)SDの影響線
せん断力SDが生じないようにD点を仮想的に切断します。
元の構造物に、単位の移動荷重P=1が作用することによって生じるD点のせん断力SD
及び曲げモーメントMDを仮想切断面に作用させれば、
元の2径間連続ばりと力学的に同じたわみ曲線が得られます。
つまり、仮想切断面に上側引張となるような一対のモーメント荷重MDとせん断力SDを与えます。
このときの荷重と支点反力(RA, RB, RC,P=1,SD,MD)を第1荷重群とします。
下図は、仮想切断位置Dにモーメント荷重MD、せん断力SDの方向に左右両部のたわみ角θが等しく、
かつ上下方向の変位の和が1(⊿=⊿1+⊿2=1)の変位を与える大きさのP
及びモーメント荷重Mを作用させたときのたわみ曲線を示しています。
このときの荷重と支点反力(RA,RB,RC,P,M)を第2荷重群とします。
以上より、構造物のある点に生じている力(断面力、反力)の影響線を求めるには、
その力だけが生じないような構造系を考え、
その力の方向に対する単位の相対変位(⊿=1またはθ=1)を
与えたときのたわみ曲線の符号を変えたものを求めればよい。
トップページ