







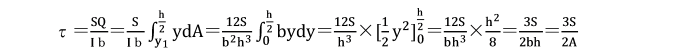





【例題6−1】
等分布荷重qが載荷されている単純ばりの中央点Cの曲げモーメントによるたわみ及びせん断力によるたわみを求めよ。
ただし、はり全体にわたり曲げ剛性(EI)は一様です。
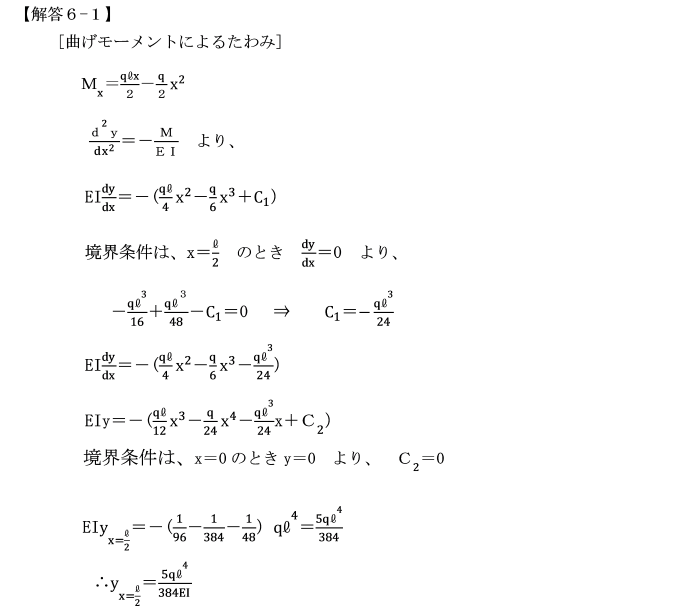

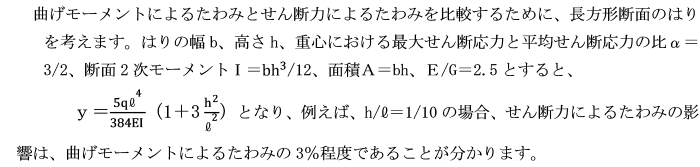

【例題6−2】
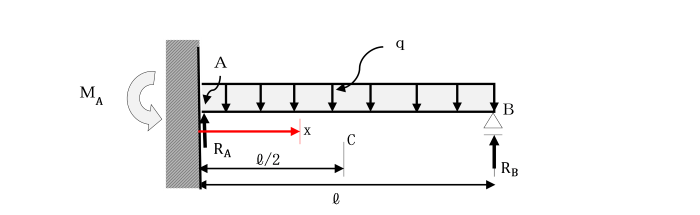
等分布荷重qが載荷されている不静定ばりの中央点Cの曲げモーメントによるたわみ及びせん断力によるたわみを求めよ。
ただし、はり全体にわたり曲げ剛性(EI)は一様です。
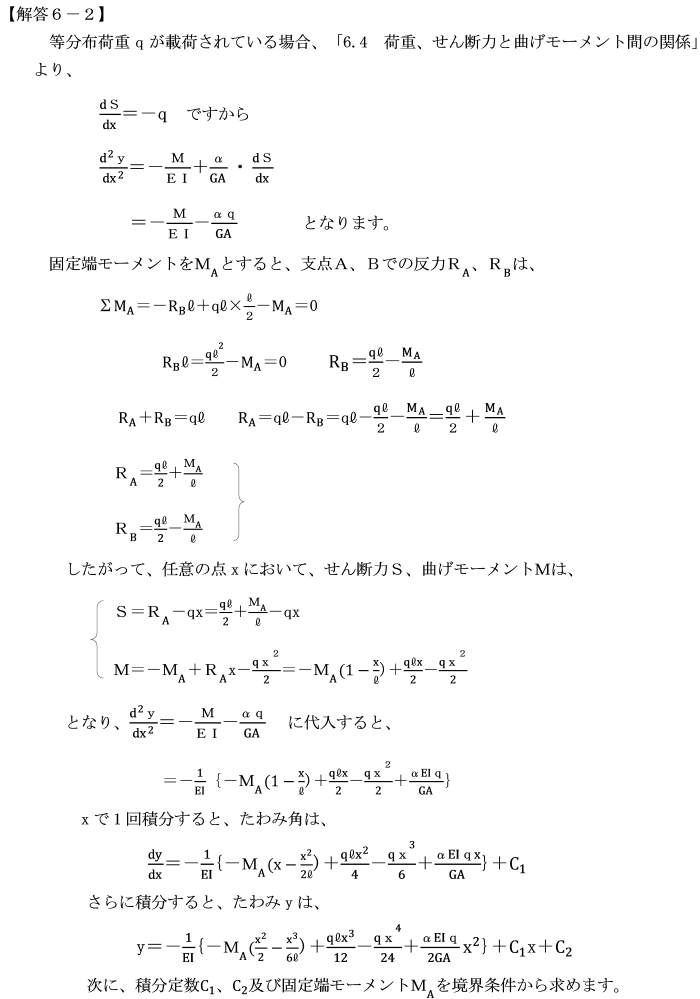
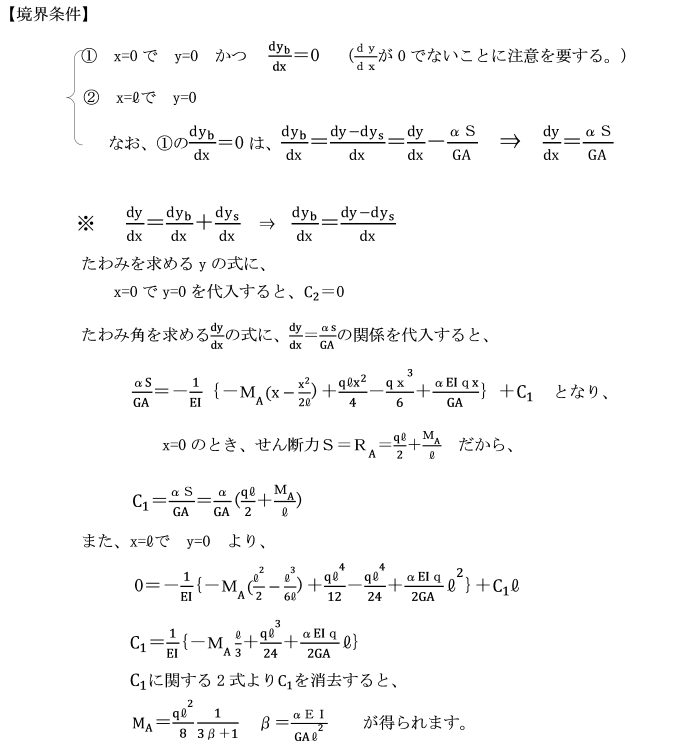


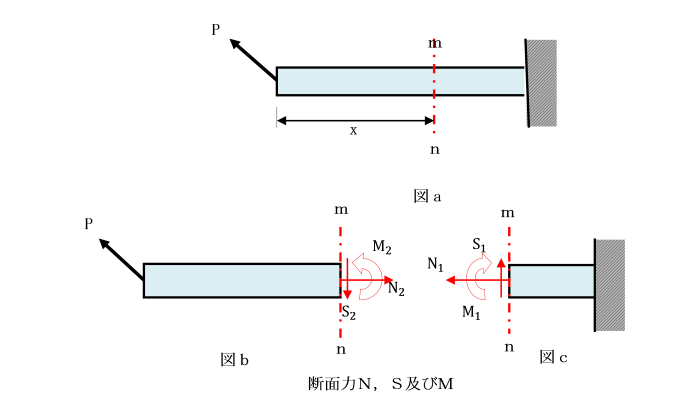
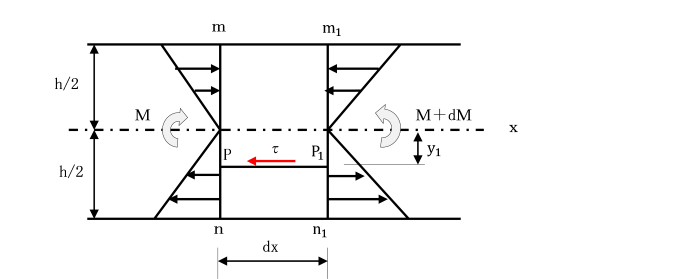
分布荷重q、せん断力S及び曲げモーメントMの関係】
dS/dx=−q dM/dx=S → d2 M/dx2 =dS/dx=−q
上の式を1つの式にまとめると、 d2 M/dx2 =−q