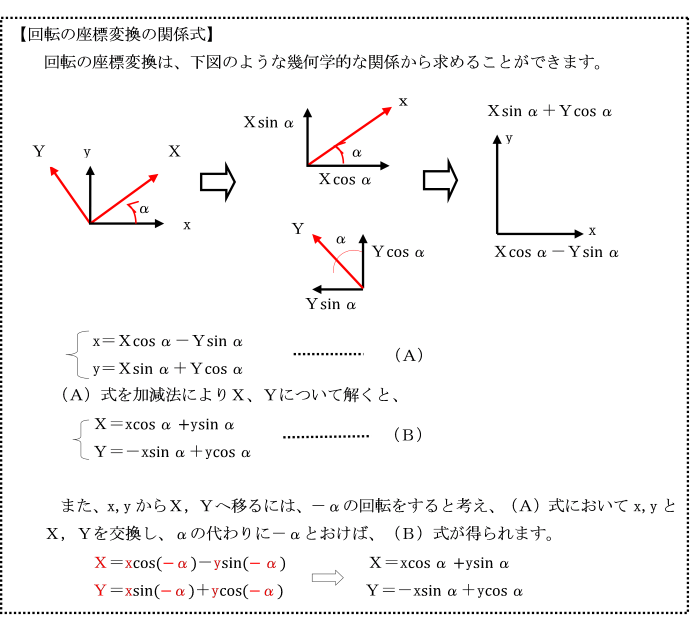
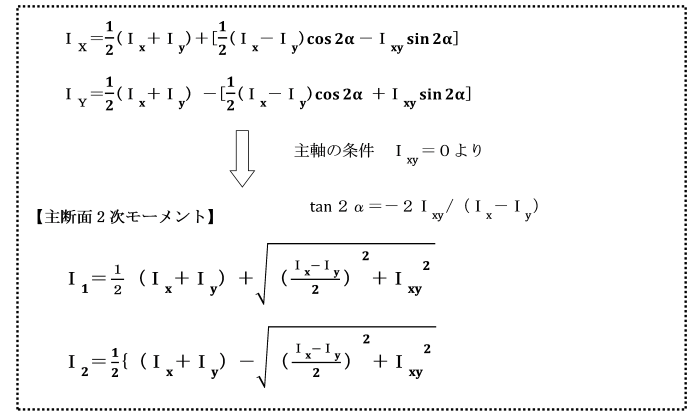
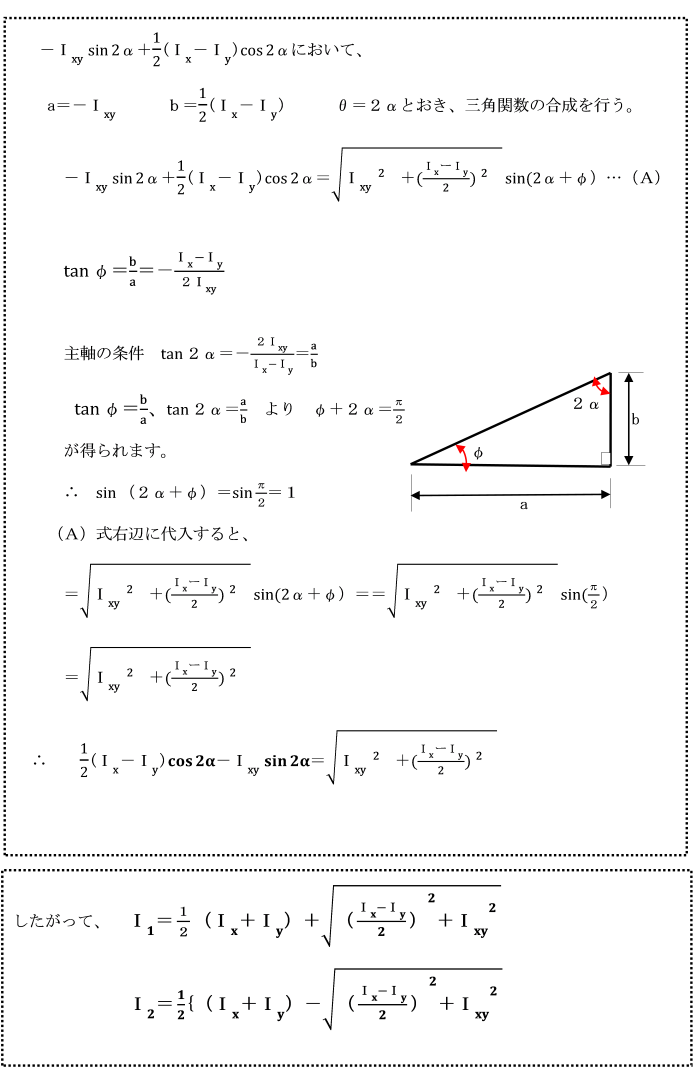
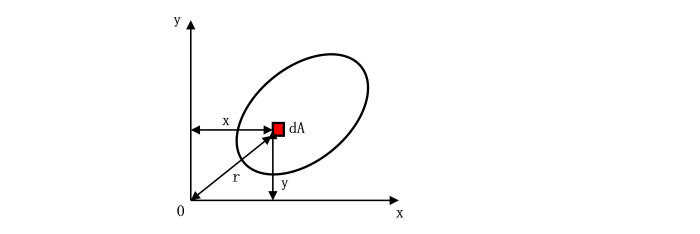
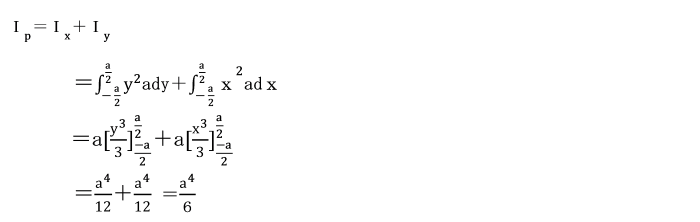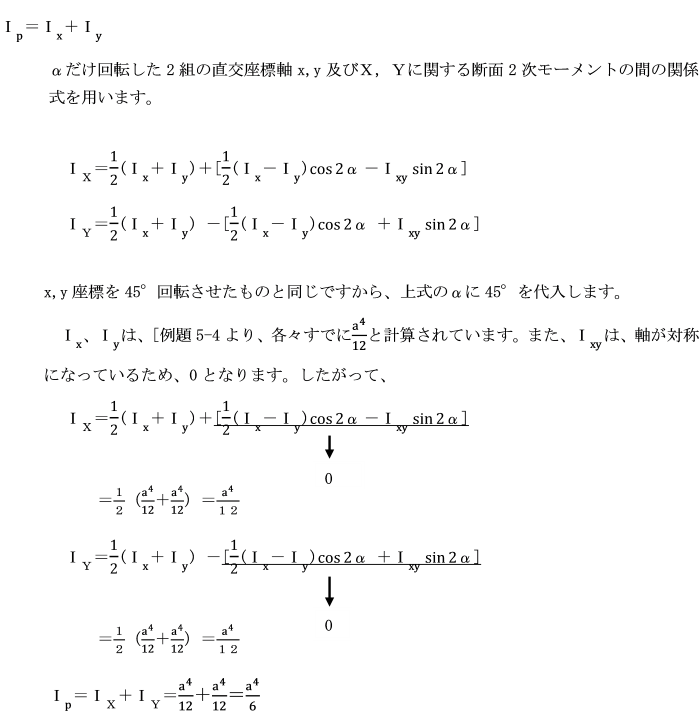丂偡側傢偪堷挘傝偁傞偄偼埑弅丄嬋偘丄偣傫抐側偳偵懳偟偰丄
丂埨慡偱椡妛揑岠棪偺椙偄抐柺宍忬傪慖傃丄悺朄傪寛掕偟側偗傟偽側傝傑偣傫丅
丂傑偨丄晹嵽偼丄偝傑偞傑側岠棪偺椙偄抐柺宍忬偑岺晇偝傟偰偄傑偡丅
丂偼傝偵嶌梡偡傞壸廳偼丄幉曽岦乮挿庤曽岦乯偱偼側偔幉捈妏曽岦偵嶌梡偟傑偡丅
丂偮傑傝墶壸廳偲偄傢傟傞傕偺偱丄廤拞壸廳丄暘晍壸廳丄儌乕儊儞僩壸廳側偳偑偁傝傑偡丅
丂墶壸廳偑嶌梡偡傞偙偲偵傛傝丄
丂偼傝偺抐柺偵偼嬋偘儌乕儊儞僩偑惗偠傑偡丅
丂偼傝偼丄嬋偘儌乕儊儞僩偵傛偭偰墶壸廳傪悈暯偵揱払偡傞峔憿暔偱偁傝丄
丂晹嵽偺忋懁丄壓懁偵嵟戝偺嬋偘墳椡偑惗偠傑偡丅
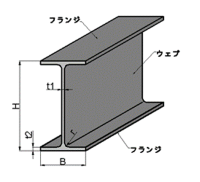
丂揝崪峔憿偺偼傝偵偼丄傛偔俫宍峾偲偄傢傟傞嵽椏偑巊傢傟傑偡丅
丂偙傟偼丄晹嵽偺忋壓抂偵偁傞僼儔儞僕晹暘偵懡偔偺柺愊傪妱傝摉偰丄
丂嬋偘儌乕儊儞僩偵懴偊傞峔憿偲側偭偰偄傑偡丅
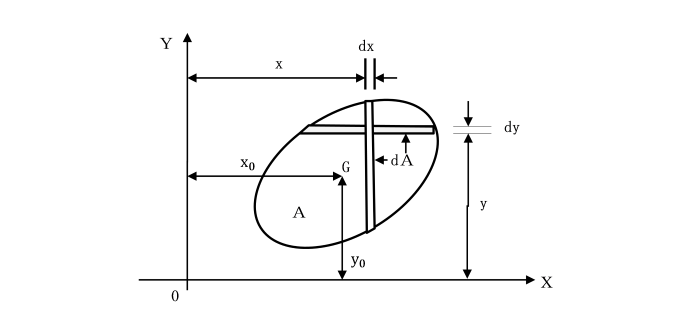
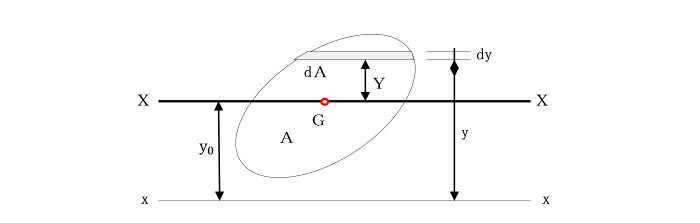
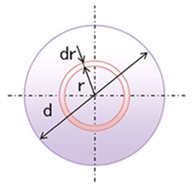
丂偼傝抐柺偺帩偮嬋偑傝偵偔偝偺惈幙偼丄
丂抐柺俀師儌乕儊儞僩偲偄偆僷儔儊乕僞偱昞尰偝傟傑偡丅
丂偙偺傛偆偵奜椡偵懳偟偰掞峈偡傞偨傔偵偼丄
丂晹嵽偺宍忬摍丄抐柺偺彅惈幙傪嵟戝尷偵妶偐偟偰愝寁偡傞昁梫偑偁傝傑偡丅
丂偦傟偱偼丄宱嵪揑側抐柺偱嫮搙傪忋偘傞偨傔偵偼丄
丂偳偺傛偆側岺晇偑側偝傟偰偄傞偺偩傠偆偐丅
丂椺偊偽丄侾偮偺晹嵽偵懳偟奜椡偑嶌梡偟偨偲偒丄
丂摨偠抐柺愊偺晹嵽偱偁偭偰傕丄
丂抐柺偑廲挿偵側偭偰偄傞偐墶挿偵側偭偰偄傞偐偱丄
丂晹嵽偺偨傢傒曽偼堎側傝傑偡丅
丂嬋偘丄偨傢傒側偳偺曄宍偟傗偡偝偺搙崌偄傪悢抣揑偵昞尰偱偒傞傕偺偑偁傟偽丄
丂嬋偘曄宍偵懳偟偰偳偺掱搙懴偊傜傟傞偐傪敾抐偡傞僷儔儊乕僞偲側傝傑偡丅
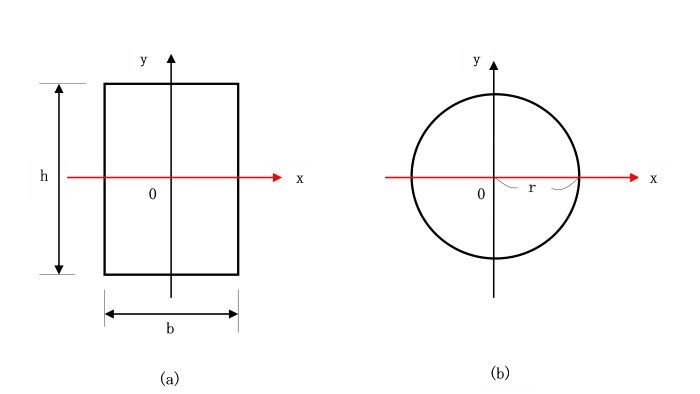
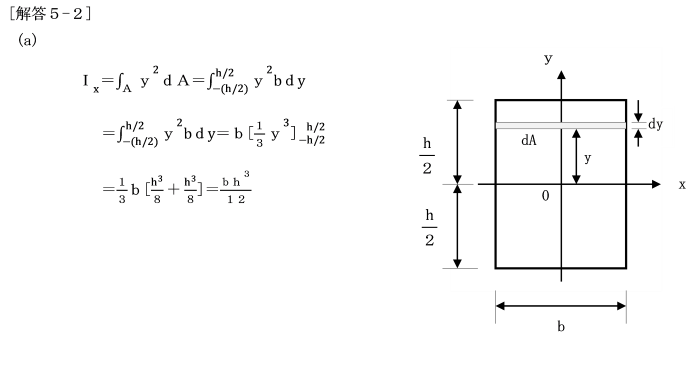
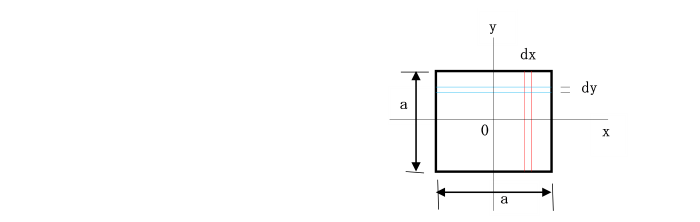
丂偙偺復偱偼丄偙偺條側抐柺偺摿惈傪昞偡偝傑偞傑側抐柺彅検偵偮偄偰傒偰偄偒傑偟傚偆丅