



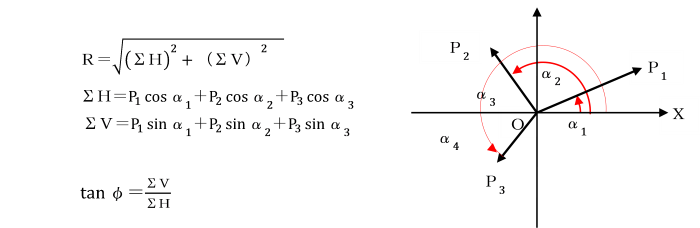


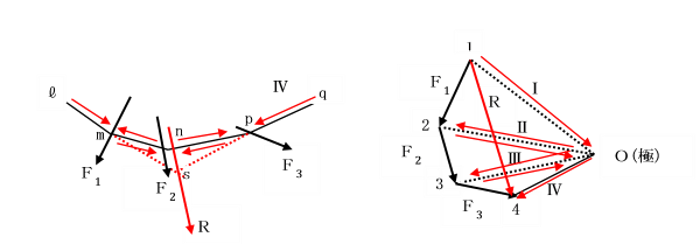
【例題1-1】
一点に作用しない3つの力F1、F2、F3の合力Rの作用線が、
連力図の最初の辺lmと最終の辺pqの交点Sをとおることを証明せよ。
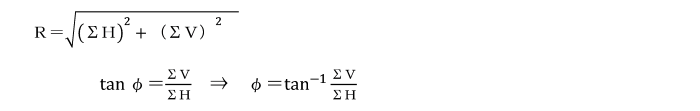
[バリニオンの定理]
個々の力に任意点からの距離を乗じたモーメントの和は、合力の任意点からの距離を乗じたモーメントに等しい。
※ 任意点に関するモーメントの和をΣMとすれば、任意点からの合力Rの作用線の垂直距離dは、 d=ΣM/R
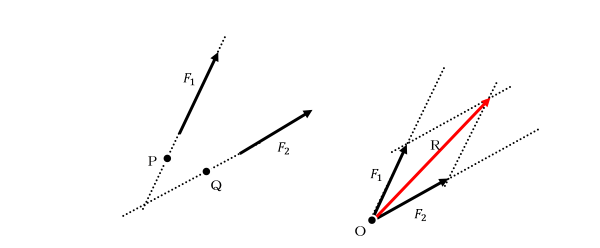
【例題1-2】
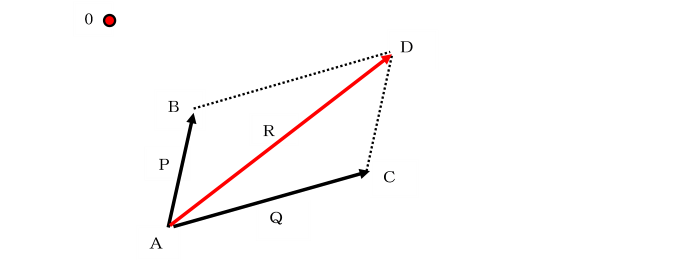
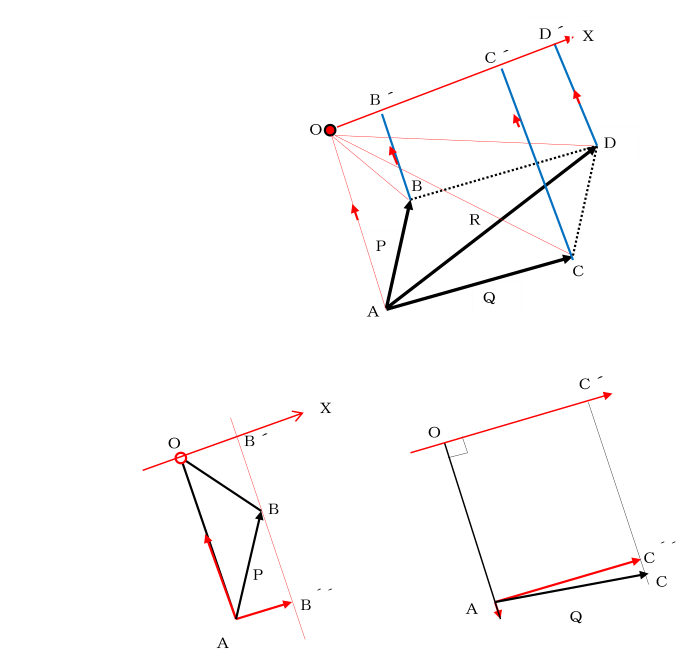
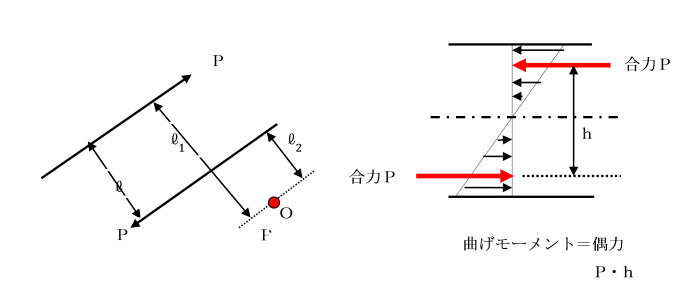
点Aで交わる2つの平面力PとQの合力をRとするとき、
平面内に選んだ任意の点Oに関するPとQのモーメントの和は、
合力Rのモーメントに等しいこと(バリニオンの定理)を証明せよ。