トップページ

第１１章 ラーメン理論

11.1　ラーメンの定義と種類

　直線部材や曲線部材が節点において剛結され、
主として曲げモーメントによって外力に抵抗する骨組みをラーメンといいます。
そのため骨組みの形はトラス構造のように三角形の集合とする必要はありません。
　一般にラーメンは直線のはり（水平材）と
柱（鉛直材）を組み合わせた長方形状の形をしているものが多い。
なお、曲線状のはりや柱を組み合わせた構造は、アーチと呼ばれ、
ラーメンと区別するのが一般的です。

　各部材には、曲げモーメントのほかに軸方向力、せん断力が生じますが、
軸方向力による部材方向の長さの変化とせん断力による部材変形は、
曲げ変形に比較して非常に小さいので、実用上問題はありません。

　ある平面内に存在するラーメンを平面ラーメンと呼びます。
実際の構造物は、立体的な構造が多いが、
これらの多くは平面ラーメンの集合体に分けることができます。
ここでは、平面ラーメンの面内変形を取り扱います。

11.2 静定ラーメン

　つり合い条件式で反力や断面力を算定できるものを静定ラーメンといいます。
静定ラーメンの例をあげます。

11.3 不静定ラーメン

　ラーメンは一般に高次の不静定構造物となり、不静定次数ｎは次の式で求められます。
　　ｎ＝ｒ＋ｋ−３ｑ
　　　ｒ：支点の拘束度の総和（可動支点：１、回転支点：２、固定支点：３）
　　　ｋ：節点の拘束度の総和（ヒンジ２、剛結３）
　　　ｑ：部材総数


【解答】

　　ｎ＝ｒ＋ｋ−３ｑ
　　　ｒ：支点の拘束度の総和（可動支点：１、回転支点：２、固定支点：３）
　　　ｋ：節点の拘束度の総和（ヒンジ２,剛結３）
　　　ｑ：部材総数

　　（１）ｎ＝ｒ＋ｋ−３ｑ
　　　　　　＝（２＋１）＋（３＋３）−３×３
　　　　　　＝０

　　（２）ｎ＝ｒ＋ｋ−３ｑ
　　　　　　＝（２＋２）＋（３＋３）−３×３
　　　　　　＝１

　　（３）ｎ＝ｒ＋ｋ−３ｑ
　　　　　　＝（３＋３）＋（３＋３）−３×３
　　　　　　＝３

　　（４）ｎ＝ｒ＋ｋ−３ｑ
　　　　　　＝（２＋１）＋（３＋３＋３＋３）−３×４
　　　　　　＝３

　　（５）ｎ＝ｒ＋ｋ−３ｑ
　　　　　　＝（２＋２）＋（２＋２）−３×３
　　　　　　＝−１

　　（６）ｎ＝ｒ＋ｋ−３ｑ
　　　　　　＝（２＋２＋２＋２）＋（３＋３＋３＋３＋３＋３）−３×７
　　　　　　＝５

　　（７）ｎ＝ｒ＋ｋ−３ｑ
　　　　　　＝（２＋２）＋（３＋３＋２＋２）−３×４
　　　　　　＝２

　　（８）ｎ＝ｒ＋ｋ−３ｑ
　　　　　　＝（２＋２）＋（３＋２＋３）−３×４
　　　　　　＝０

　　（９）ｎ＝ｒ＋ｋ−３ｑ
　　　　　　＝（２＋３＋３＋１）＋（３＋３＋２＋３＋３）−３×６
　　　　　　＝５

11.4　静定ラーメンの解法

11.4.1 部材力の解析

図のような等分布荷重qが載荷されている門型ラーメンの部材力を求めます。

　柱部材ではラーメンの内側がはりの下側に相当します。
つまり、軸方向力図（Ｎ図）、せん断力図（Ｓ図）は、（−）は内側、（＋）は外側に描き、
曲げモーメント図（Ｍ図）は引張側を内側（＋）、圧縮側を外側（−）に描きます。

　断面力の計算は、求めようとする部材の外側が上部になるように
水平に置き換えて考えると分かりやすい。
ある断面の部材力を計算する際には、
その断面の一方の側にある外力（支点反力も含む）全てを考えることが大事です。

　例えば、図のような静定ラーメンのｍ−ｍ断面の断面力を求める場合、
断面の左側にある外力全てを考えると、部材ＡＢ、ＢＥ間の外力全てが対象となります。
また、断面の右側を考えると、部材ＥＣ、ＣＤ間の外力全てが対象となります。
検討する断面の位置により適宜どちらの側かを選べばいい。

　図のようなラーメンにおいて、
　まず、支点反力を求めます。静的な力のつり合い条件は、
　　ΣＸ＝０：　　　ＨA 　＝０
　　ΣＹ＝０：　　　ＶA ＋ＶD−ql＝０
　　ΣＭD＝０： 　　ＶA l − ql2/２＝０
　　　　　　　　　　ＶA ＝ＶD＝ql/２

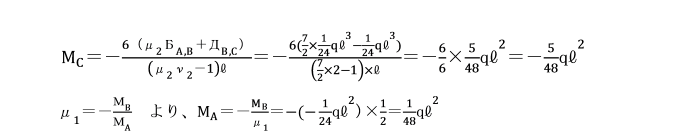
１．軸方向力：Ｎ
　[求め方]　ある断面の一方の側にある軸方向力の和
　[符号の約束]
　　ある断面に対し、向かってくる力（圧縮力）は（−）、遠ざかる力（引張力）は（＋）とする。

２．せん断力：Ｓ
　[求め方]　ある断面の一方の側にある垂直力の和
　[符号の約束]
　　左側から求める場合：上向き（＋）、下向き（−）
　　右側から求める場合：上向き（−）、下向き（＋）

３．曲げモーメント：Ｍ
　[求め方]　ある断面の一方の側のモーメントの和
　[符号の約束]
　　左側から求める場合：時計回り（＋）、反時計回り（−）
　　右側から求める場合：時計回り（−）、反時計回り（＋）

　支点反力が求まったので、次に部材ごとに断面力を求めます。

　（ａ）部材ＡＢ：
　　　支点Ａから節点Ｂ方向に座標軸ｘをとり、断面の下側（支点Ａ側）を考えると、
　　　この点の曲げモーメントＭx、せん断力Ｓx、軸方向力Ｎxは、はりと同じようにして、
　　　Ｍx＝ＨA・ｘ＝０
　　　Ｓx＝ＨA＝０
　　　Ｎx＝−ＶA＝−ql/２　ですから、
　　　部材ＡＢには、曲げモーメントもせん断力も生じません。
　　　また、ＶA＝ql/２であるから、軸方向力はＮ= −ql /２ となります。
　　　（−）記号は、圧縮力であることを示しています。
　（ｂ）部材ＢＣ：
　　　節点Ｂから節点Ｃ方向に座標軸ｘをとり、断面の左側（節点Ｂ側）を考えると、
　　　点ｘでの曲げモーメントＭx、せん断力Ｓx 、軸方向力Ｎxは、
　　　Ｍx＝ＨAh＋ＶAｘ(−qｘ)ｘ/２＝ｑlｘ/２−qｘｘ/２＝qｘ(l−ｘ）/２
　　　Ｓx＝ＶA−qｘ＝q（l/２−ｘ）
　　　Ｎx＝ＨA＝０
　　　したがって、Ｍxはｘ＝l/2で最大値ql2/8をとります。
　　　　※　(dＭx)/dx＝ql/２−qx (dＭx)/dx＝０　より、x＝l/2　のときＭxは最大
　　　せん断力は、点Ｂ（ｘ＝０）では、ql/2、点Ｃ（ｘ＝l）では、−ql/2となります。
　　　軸方向力は０となります。
　　　曲げモーメント、せん断力は単純ばりに等分布荷重が作用する場合と同じです。
　（ｃ）部材ＣＤ：
　　　節点Ｃから支点Ｄ方向に座標軸ｘをとり、断面の上側（節点Ｃ側）を考えると、
　　　点ｘでの曲げモーメントＭx、せん断力Ｓx、軸方向力Ｎxは、
　　　Ｍx＝ＨA(h−ｘ）＋ＶA−ql/２＝ｑl2/２−ｑl2/２＝０
　　　Ｓx＝-ＨA＝０
　　　Ｎx＝ＶA−ql＝ql/２−ｑl＝−ql/２
　　　これは、部材ＡＢ、ＢＣと同じように、部材の左から右に座標軸ｘをとった場合です。
　　　しかし、部材ＣＤは、支点Ｄから節点Ｃの方向に座標軸ｘをとる方が計算が簡単です。
　　　この場合、支点Ｄからｘの距離における、曲げモーメントＭx、せん断力Ｓx は、
　　　支点Ｄで水平反力が存在しないから、
　　　Ｍx＝０ 、Ｓx＝０ となり、
　　　軸方向力は断面に対し向かってくる力ですから、
　　　Ｎx＝−ＶD＝−ｑl/２ となり、同じ結果が得られます。
　　以上より、Ｍ図、Ｓ図、Ｎ図は次のようになります。
（２）水平方向に集中荷重を受ける静定ラーメン
　　　静的な力のつり合い条件は、
　　　ΣＸ＝０：　−ＨA＋Ｐ＝０
　　　ΣＹ＝０：　ＶA＋ＶD＝０
　　　ΣＭD＝０： ＶAl＋Ｐｈ＝０
　　　∴　ＨA＝Ｐ
　　　　　ＶA＝−Ｐｈ/l
　　　　　ＶD＝Ｐｈ/l
支点反力が求まったので、次に部材ごとの断面力を求めます。
　　(a）部材ＡＢ：
　　　支点Ａから節点Ｂの方向に座標軸ｘをとり、断面の下側（支点Ａ側）を考えると、
　　　Ｍx＝ＨA・ｘ＝Ｐｘ
　　　Ｓx＝ＨA＝Ｐ
　　　Ｎx＝−ＶA＝Ｐｈ/l
　　　したがって、節点ＢではＭB＝Ｐｈ　となります。
　　　部材ＡＢの中間には水平力は作用していないから、部材の全長にわたり、せん断力はＳ＝Ｐです。
　　　支点Ａでは下向きに反力が作用するから、軸方向力はN＝Ph /lと正になります。
　　(ｂ）部材ＢＣ：
　　　節点Ｂから節点Ｃの方向に座標軸ｘをとり、断面の左側（節点Ｂ側）を考えると、
　　　節点Ｂからｘの距離における曲げモーメントＭx、せん断力Ｓx 、軸方向力 Ｎxは、
　　　Ｍx＝ＨA・ｈ＋ＶA・ｘ＝Ｐｈ−Ｐｈ/lｘ
　　　Ｓx＝ＶA＝−Ｐｈ/l
　　　Ｎx＝ＨA−Ｐ＝Ｐ−Ｐ＝０
　　　したがって、　ＭB＝Ｐｈ　　ＭC＝０　です。
　　　ＭC＝０であることは、支点Ｄに水平力が存在しないことからも分かります。
　　　部材ＢＣに軸方向力が生じないのは、水平力Ｐが全て部材ＡＢによって分担されるためです。
　　(ｃ）部材ＣＤ：
　　　支点Ｄから節点Ｃの方向に座標軸ｘをとり、断面の下側（支点Ｄ側）を考えると、
　　　支点Ｄからｘの距離における曲げモーメントＭx、せん断力Ｓxは、
　　　支点Ｄで水平反力が存在しないから、Ｍx＝0、Ｓx＝0となります。
　　　鉛直反力ＶD＝Ｐｈ/l が作用するので、軸方向力Ｎx＝−Ｐｈ/l が生じます。
　　以上より、Ｍ図、Ｓ図、Ｎ図は次のようになります。

11.5　不静定ラーメンの解法

　　　ラーメンに外力が作用するとき、その部材内に生じる応力の算定には、
　　応力法と変位法があります。
　　ラーメンの形状が簡単な場合には前者によっても後者によっても大差はありませんが、
　　複雑なラーメンとなると前者にはその実用性がなく、専ら後者によることになります。

　　　応力法には、カスティリアノの第２定理（最小仕事の原理）、
　　単位荷重法、三連モーメントの定理などによる解法があります。
　　これらは、曲げモーメントあるいは反力などを未知量とする解法です。
　　これに対し、変位法には、たわみ角法、モーメント分配法、定点法があり、
　　節点及び部材角を未知量とする解法です。

　　　応力法では、未知数の個数は構造物の不静定次数に等しい。
　　変位法に属するたわみ角法では、
　　未知数の個数は、一般に不静定次数よりも少なくなります。
　　そのためたわみ角法は、高次の不静定ラーメンの応力算定に用いるとその威力を発揮します。
　　各種解法によりひじ型ラーメンを解き、それぞれの解法の特質を理解しましょう。

11.5.1 応力法

T　単位荷重法による解法

　　単位荷重法による解法は、不静定次数の数だけ不静定力を取り除き、
　静定基本系を設定します。
　次に、静定基本系に元の構造体系から不静定力を取り除いた箇所に、
　単位の不静定力を作用させます。
　不静定力として取り除いた点の変位、回転角を求め、
　実際の構造上の境界条件との整合を図れる方程式、
　いわゆる弾性方程式から不静定力を求めます。

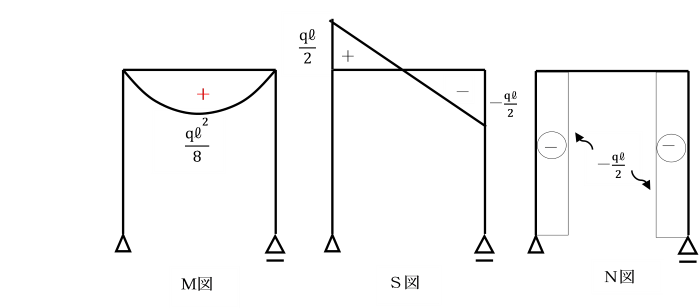
【例題】
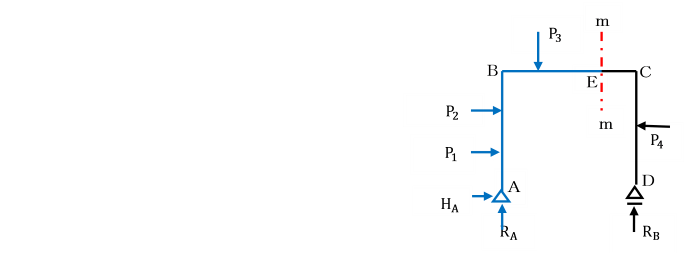
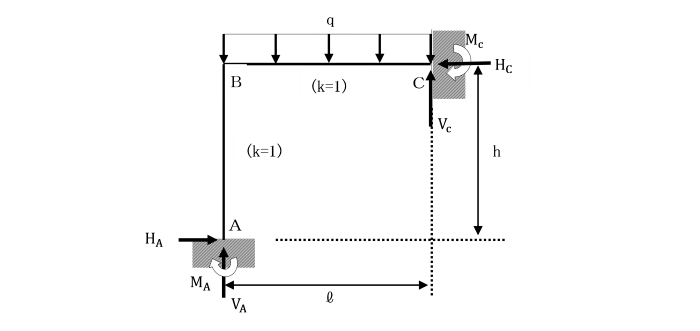
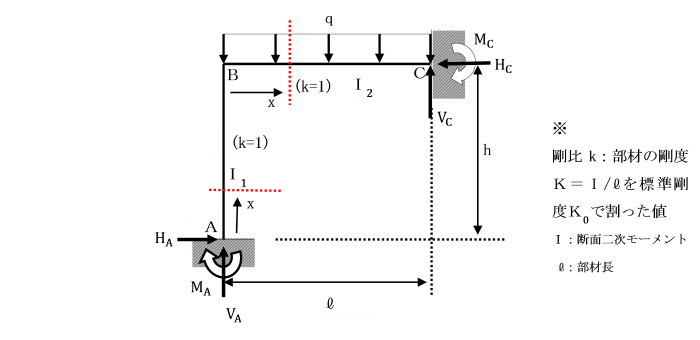
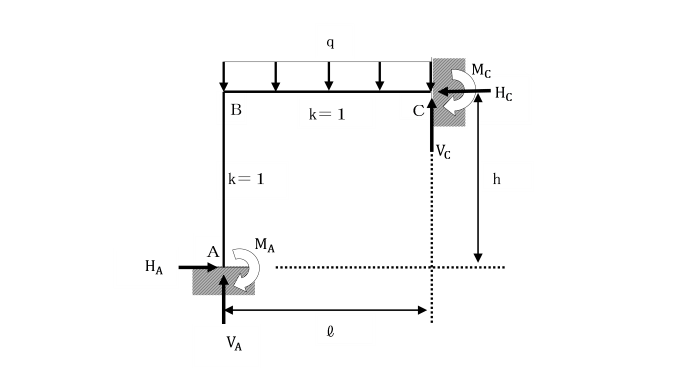
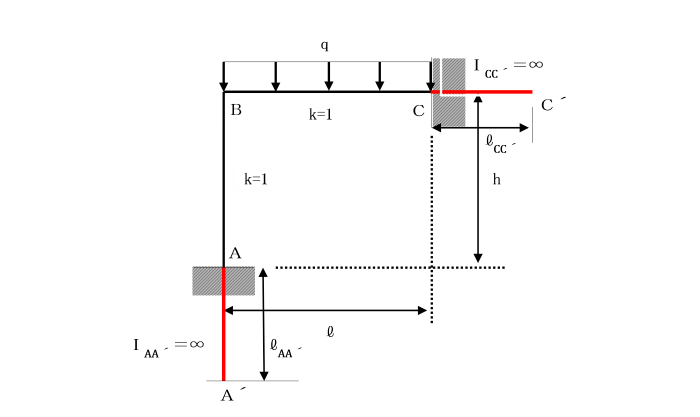
　　支点Ａ及びＣで固定されているひじ形ラーメンの水平部材に等分布荷重ｑが作用しています。
　　基準部材に対する各部材の剛比kはいずれも１として、単位荷重法により解きましょう。

【解答】
　　　不静定次数ｎの計算
　　　　ｎ＝ｒ＋ｋ−３ｑ＝（３＋３）＋３−３×２＝３　３次不静定構造物
　　　　ｒ：支点の拘束度の総和（可動支点：１、回転支点：２、固定支点：３）
　　　　ｋ：節点の拘束度の総和（ヒンジ２、剛結３）
　　　　ｑ：部材総数

　　　　支点Ｃの鉛直反力ＶC、水平反力ＨC及びモーメントＭCを不静定力に選びます。
　　　　すると図のような静定基本系を得ます。

　　　次に静定基本系に単位の不静定力
　　　　Ｘ1＝１（VC方向）、Ｘ2＝１（HC 方向）、Ｘ3＝１（ＭC 方向）が作用するときの載荷状態
　　　　及びそのときの曲げモーメント図（Ｍ1図、Ｍ2図及びＭ3図）を示す。
　　　ここで、単位荷重法を用いて、点Ｃの鉛直変位V、水平変位H及び
　　　回転変位θCを求めます。
　　　静定基本系に４つの荷重q,Ｘ1,Ｘ2,Ｘ3が同時に作用したときの点Ｃの鉛直変位vは、
　　　重ね合わせの原理により、次のようになります。
　　　鉛直変位　V＝10＋δ11＋δ12＋θ13

　　　ここで、10は、図１の荷重載荷状態での点Ｃの鉛直変位、
　　　δ11は、図２の荷重載荷状態での点Ｃの鉛直変位、
　　　δ12は、図３の荷重載荷状態での点Ｃの鉛直変位、
　　　θ13は、図４の荷重載荷状態での点Ｃの鉛直変位。
　　　同様に水平変位H及び回転変位θCは次式で表されます。
　　　水平変位　H＝20＋δ21＋δ22＋θ23

　　　ここで、20は、図１の荷重載荷状態での点Ｃの水平変位、
　　　δ21は、図２の荷重載荷状態での点Ｃの水平変位、
　　　δ22は、図３の荷重載荷状態での点Ｃの水平変位、
　　　θ23は、図４の荷重載荷状態での点Ｃの水平変位。
　　　回転変位　θC＝30＋δ31＋δ32＋θ33

　　　ここで、30は、図１の荷重載荷状態での点Ｃの回転変位、
　　　δ31は、図２の荷重載荷状態での点Ｃの回転変位、
　　　δ32は、図３の荷重載荷状態での点Ｃの回転変位、
　　　θ33は、図４の荷重載荷状態での点Ｃの回転変位。
　　　剛比kが１ということは、(Ｉ1/h)/(Ｉ2/l)＝Ｉ1l/Ｉ2 h＝1　が成立し、
　　　1/Ｉ2＝h/lＩ1　の関係を次式に代入し、Ｉ1で整理します。
　　　実際、点Ｃは固定端ですから、鉛直変位V、水平変位H及び
　　　回転変位θCは０でなければなりません。
　　　したがって、上式より次の弾性方程式が得られます。
　　　Ｘ1,Ｘ2,Ｘ3に関する３元連立1次方程式を解けば、
　　　残りの支点反力及び断面力を求めることができます。
　　　式を整理すると、次の弾性方程式が得られます。
　　　　32Ｘ1＋12hＸ2-36Ｘ3＝15ql2
　　　　6lＸ1＋ 4hＸ2- 6Ｘ3＝ 3ql2
　　　　9lＸ1＋ 3hＸ2-12Ｘ3＝ 4ql2
　　　となり、Ｘ1,Ｘ2,Ｘ3について解くと、
　　　Ｘ1＝9ql/16　　　Ｘ2＝ql2/16h　 　　Ｘ3＝5ql2/48　　となります。

U　カスティリアの第２定理（最小仕事の原理）による解法

　δi＝∂Ｕ/∂Ｐi 　は、カスティリアノの第２定理と呼んでいます。
　つまり、線形構造物に対しては、
　任意荷重Ｐiに関するひずみエネルギーＵの偏微分係数は、対応する変位δiに等しい。
　カスティリアノの第２定理は、
　構造物の変形量を求めるのに応用されます。
　不静定構造物のひずみエネルギーＵを、
　変位が拘束される不動点（変位＝０）に作用する不静定力の関数で表し、
　ひずみエネルギーＵを不静定力で偏微分した値は０になります。
　これが最小仕事の原理であり、
　カスティリアノの第２定理を構造物の不動点に応用した特別の場合です。
　この解法原理を用いて、例題のラーメンに適用してみましょう。

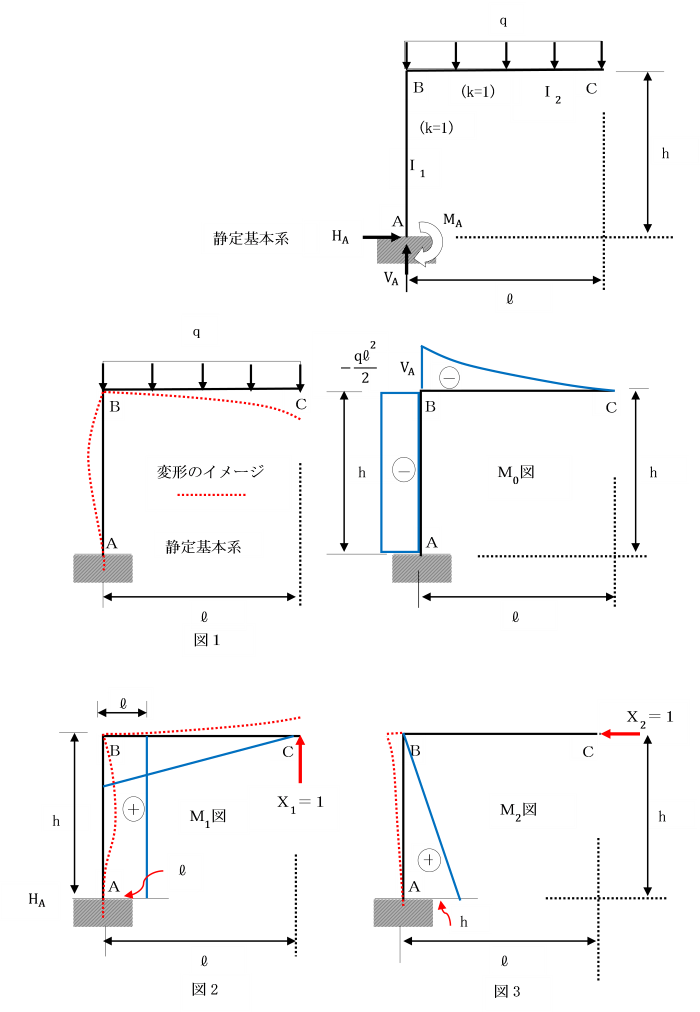
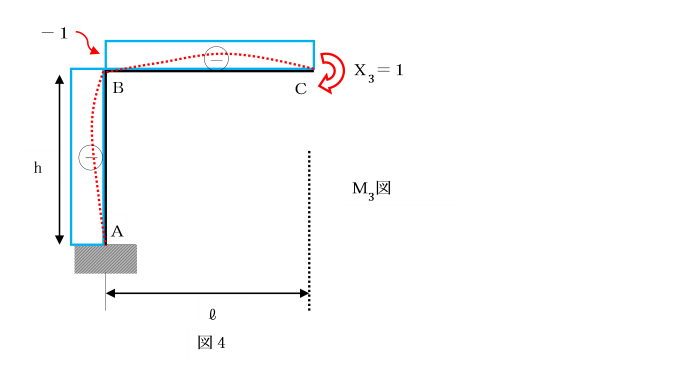
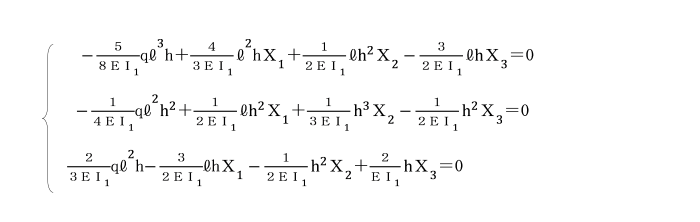
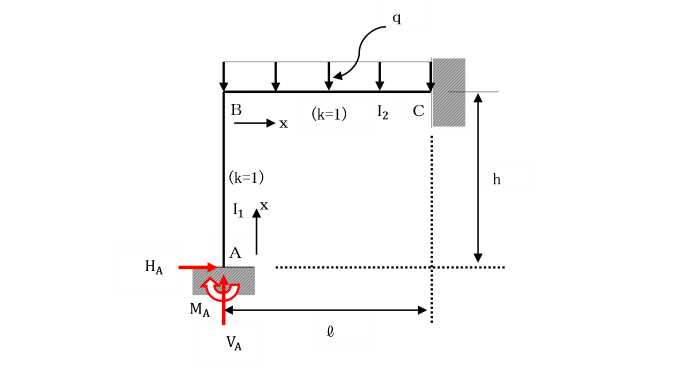
【例題】
　　支点Ａ及びＣで固定されているひじ形ラーメンの水平部材に等分布荷重ｑが作用しています。
　　基準部材に対する各部材の剛比kはいずれも１として、
　　カスティリアノの第２定理（最小仕事の原理）により解きましょう。

【解答】
　　　不静定次数ｎの計算
　　　　ｎ＝ｒ＋ｋ−３ｑ
　　　　　ｒ：支点の拘束度の総和（可動支点：１、回転支点：２、固定支点：３）
　　　　　ｋ：節点の拘束度の総和（ヒンジ２、剛結３）
　　　　　ｑ：部材総数
　　　　　ｎ＝ｒ＋ｋ−３ｑ＝（３＋３）＋３−３×２＝３
　　　　このラーメンは３次不静定構造物ですから、
　　　　鉛直反力ＶAと水平反力ＨA及び曲げモーメントＭAを不静定力に選びます。

　　　　柱ＡＢとはりＢＣの曲げモーメントＭ1,Ｍ2は次のようになります。
　　　　柱ＡＢ　：Ｍ1＝ＭA−ＨA・x
　　　　はりＢＣ：Ｍ2＝ＶA・x−qx2/２＋ＭA−ＨA・h

V　三連モーメントの定理による解法

　三連モーメントの定理は、モーメントを未知数にとった
　不静定ばりの解法であり、応力法の一つです。
　互いに隣り合う三つの支点に働く曲げモーメントＭA,ＭB,ＭCを関連づけ、
　一般式は次のように表されます。

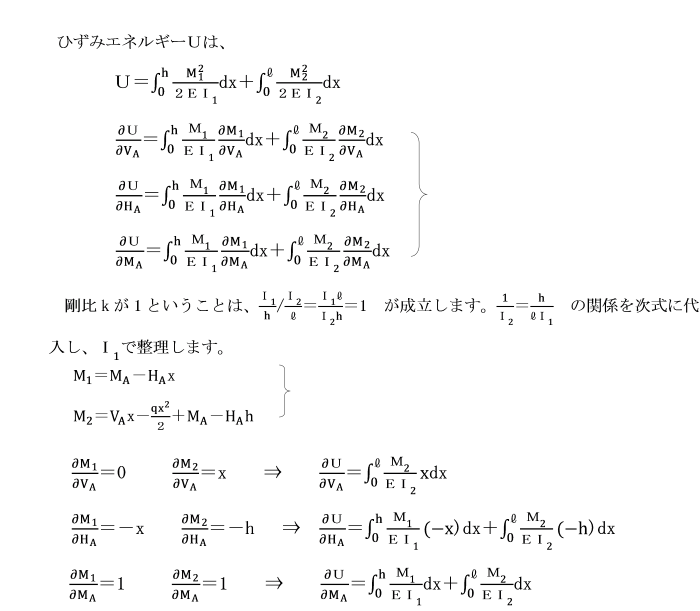
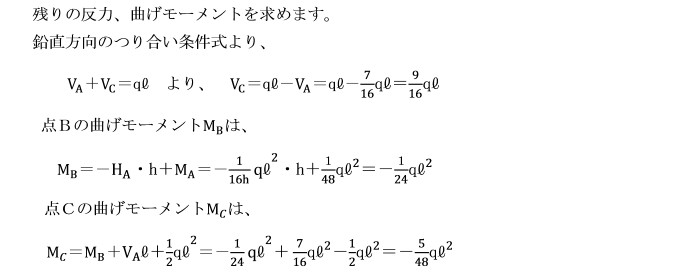
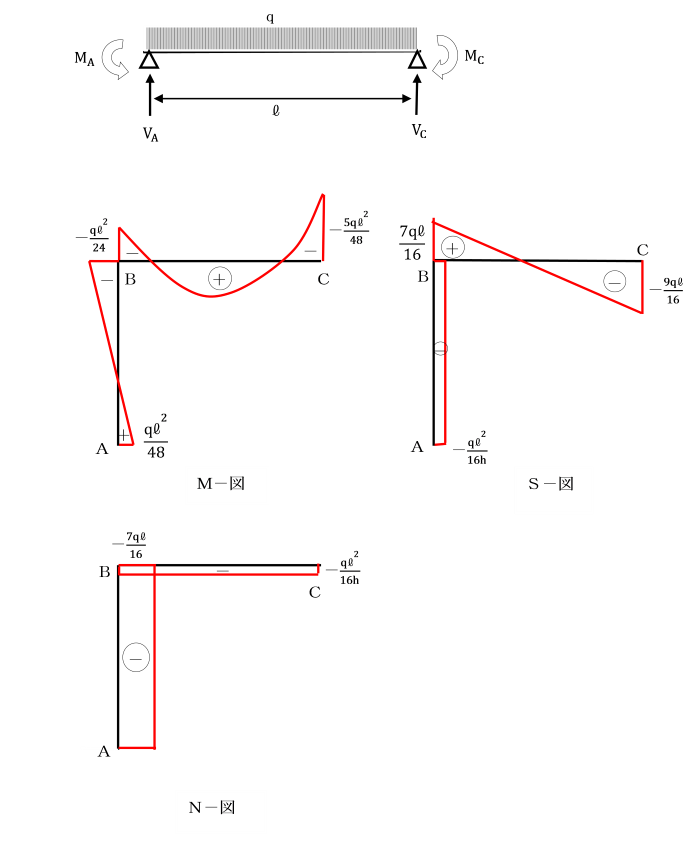
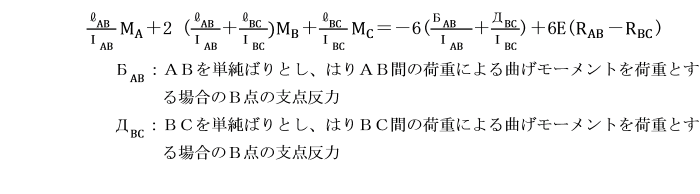
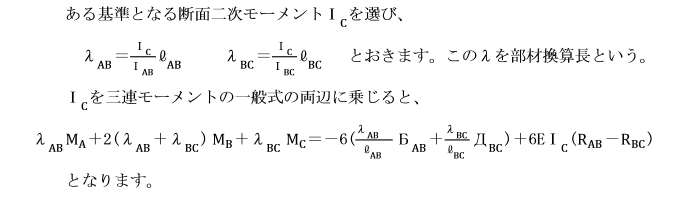
【例題】
　　支点Ａ及びＣで固定されているひじ形ラーメンの水平部材に等分布荷重ｑが作用しています。
　　基準部材に対する各部材の剛比kはいずれも１として、
　　三連モーメントの定理により解きましょう。

【解答】
　　　点Ａ、Ｃは固定端ですので、
　　　Ａ点の下側にＩAA´＝∞のはりlAA´、
　　　また、Ｃ点の右側にはＩCC´＝∞のはりlCC´があるものとして、
　　　三連モーメントの定理を適用します。

11.5.2 変位法

W　たわみ角法による解法

　【解説】
　　ラーメンの変形を考える上で重要なポイントは、
　　はりと柱の接合状態です。
　　はりと柱は剛節と呼ばれる接合がなされています。

　　剛節とは部材が節点で、
　　ガセットという板に斜材等の部材を複数のボルトで剛に連結してあるものです。
　　1つの節点に集まる部材の回転角はすべて同じで、
　　部材相互のなす角度は、変形前と変形後で変化しないで維持されます。
　　今、図のような剛節構造物のＡ点に、
　　外力Ｐが水平方向に作用しています。
　　剛節構造物は各節点で剛結されています。
　　そのため、力が伝達され外力Ｐの作用により、
　　全ての部材に対して何らかの変形が生じます。
　　今、つり合い状態にある剛節構造物から
　　１つの直線部材ＢＣを取り出してみます。
　　この場合、部材ＢＣは、節点Ｂの右側で極めて接近して、
　　また、同様に節点Ｃの左側においても極めて接近したところで仮想的に切断し、
　　取り出すものとします。
　　取り出した１つの構造部材B´C´を示す。
　　図から変形後の部材Ｂ´Ｃ´は、
　　変形前の部材ＢＣに対して角Ｒだけ回転しています。
　　部材ＢＣの相対変位を凵A部材長さを１とすれば、
　　Ｒ＝冤を部材回転角といいます。

　　次に変形後の節点Ｂ´,Ｃ´において、
　　部材のたわみ曲線に引いた接線と
　　線分Ｂ´Ｃ´のなす角τB、τCをそれぞれ接線回転角といいます。

　　また、これらの接線が変形前の部材軸線ＢＣとのなす角θB 、θCを
　　節点回転角あるいは、たわみ角といいます。
　　たわみ角θと接線回転角τ、部材回転角Ｒとの間には、

　　θB＝τB＋Ｒ　　　θC＝τC＋Ｒ　　が成立します。

　　断面には、外力Ｐの作用の影響により材端力として
　　材端モーメント、材端せん断力、材端軸方向力
　　（はり理論においては曲げモーメント、せん断力、軸方向力）が生じます。
　　剛節構造物は、一般に各節点において複数の部材が接合されているため、
　　はり理論の曲げモーメントとは別の考え方を導入します。

　　材端力（材端モーメント、材端せん断力、材端軸方向力）とは節点に作用する外力ではなく、
　　外力Ｐの作用による影響で部材に生じる力（部材の内力）で、
　　はり理論における断面力に相当するものです。
　　当然、材端力は外力が原因として生まれるものです。

　　材端モーメントの符号は、時計回りのモーメントのときに正と定めます。

　　それでは取り出した部材Ｂ´Ｃ´には、
　　どのような変形が生じているでしょうか。
　　剛節されている部材の剛度（Ｉ/l,Ｉ：断面２次モーメント,l：部材長さ）により、
　　変形は変わります。
　　例えば、柱部材がはり部材に比べ著しく剛度が高ければ、
　　はり部材のたわみ角は、固定端ばりと同様たわみ角は０に近づきます。

　　一方、柱部材の剛度がはり部材より著しく小さい場合には、
　　はりのたわみ角は、単純ばりの可動支点のようなたわみ角が生じます。
　　このように、剛節構造物の接合部分の変形は、柱とはりの相対的な剛度のバランスによって、
　　固定端に近いか、回転支点に近いかが決まります。
[たわみ角法の考え方及び基本式の誘導（１）]

　　たわみ角法は、はりと柱の両端部のたわみ角から、
　　両端部に発生する曲げモーメントを求める計算法です。
　　部材ＢＣの変形を求めるために、
　　両端が回転支点である単純ばりと仮定し、
　　外力としてモーメント荷重ＭA,ＭBを時計回りに両端に作用させます。
　　その際の両端のたわみ角は、モールの定理よりθA、θBを算出すると、

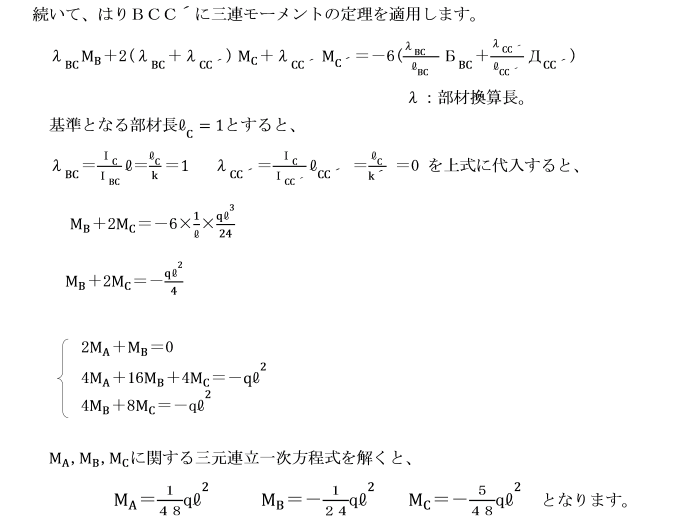
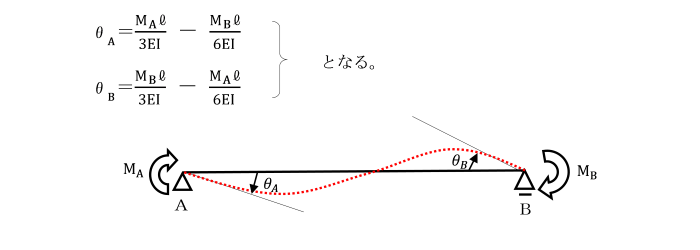
モールの定理
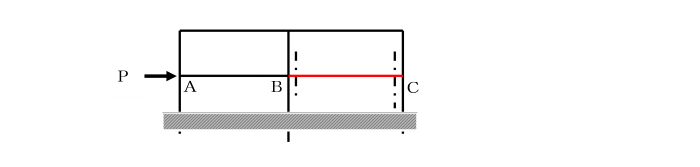
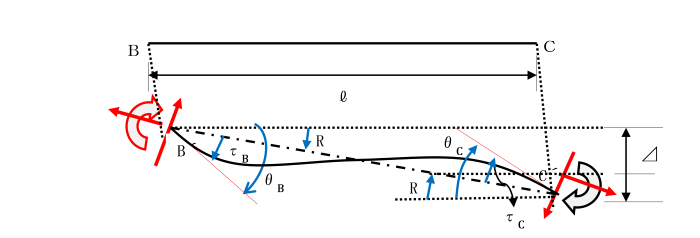
　　曲げモーメント図を曲げ剛性（ＥＩ）で割った図形を分布荷重（弾性荷重）と考え、
　　この荷重によるせん断力、曲げモーメントがそれぞれたわみ角、たわみに相当する。



　　その際、剛節構造物は、接合部に複数の部材が集結していることから、
　　はり理論のような正の曲げ（はりの下側引張り）、
　　負の曲げ（はりの上側引張り）の符号設定をすることは困難です。
　　そのため時計回りの方向を常に正と設定します。
　　先の、
　　例えば、今、１つの直線部材ＡＢを取り出し、部材ＡＢを単純ばりと考えます。
　　その単純ばりの中央に集中荷重Ｐを載荷します。
　　そのとき部材両端のたわみ角は、左端（θA)が、
　　＋Pl/16ＥＫ(時計回り)、右端（θB)が−Pl/16EＫ（反時計回り）となります。
　　部材ＡＢは、両端が回転支点である単純ばりと仮定しているため、
　　ＡＢ両端には曲げモーメントは生じません。

　　実際、部材ＡＢは、ラーメン構造として剛節されているため、
　　集中荷重Ｐが作用した場合に、
　　取り出した部材ＡＢの両端には、断面力としての材端力が生じています。
　　今、外力として作用させたモーメント荷重ＭA 、ＭBを
　　集中荷重Ｐが作用したときに両端に生じる内力として考えます。
　　そうすると、集中荷重Ｐの作用により部材ＡＢの両端に生じる内力の関係として整理できます。
　　ＭA, ＭB式は、単純ばりの両端Ａ,Ｂにモーメント荷重としてＭA 、ＭBを
　　作用させた場合のたわみ角との関係式ですが、
　　見方を変えて集中荷重Ｐが作用した際に生じる内力と考えます。
　　しかし、ＡＢは単純ばりと考えているため、
　　集中荷重Ｐによって回転支点Ａ，Ｂでは、たわみ角が生じますが、
　　モーメントＭA 、ＭBは生じません。
　　この条件を満足するように、上式ＭA,ＭBを変形すると、
　　この時点での　ＭA 、ＭBは、外力ではなく、集中荷重Ｐによって生じる内力であると考えます。
　　上式ＭA,ＭBは、θAが、＋Pl/16ＥＫ、θBが−Pl/16ＥＫの場合、
　　ＭA, ＭBの値は０となり、材端モーメントは生じていない。
　　上式ＭA,ＭBを変形すると、
　　ここで、上式においてθA、θBの値が０の場合、
　　つまり、両端固定ばりの曲げモーメントを示しています。
　　Ａ点においては、反時計回りに材端モーメントPl/8、
　　Ｂ点においては、時計回りに材端モーメントPl/8が生じます。
　　ここで、上式においてθA、θBの値が０の場合、
　　つまり、両端固定ばりの曲げモーメントを示しています。
　　Ａ点においては、反時計回りに材端モーメントPl/8、
　　Ｂ点においては、時計回りに材端モーメントPl/8が生じます。
　　ここで、ＣAB、ＣBAは、たわみ角の荷重項と呼ばれるもので、
　　θA=θB＝０　
　　つまり、両端固定の曲げモーメントに等しい。
　　また、部材の右端が左端に比べてδだけ低い位置にある場合には、
　　見かけ上、θA＝δ/l、θB＝δ/lであっても、
　　材端モーメントＭA 、ＭBには影響しないため、
　　Ｒ＝δ/l（部材回転角）として、上式に組み込むと、
　　さらに、任意に選んだ断面二次モーメントＩC及び
　　部材長lCによって基準剛度ＫC＝lC/lCを定義すると、
　　　k＝Ｋ/ＫCで与えられるkを剛比という。
　　Ｋは、剛度（Ｉ／l）。
　　ここで、
　　たわみ角の基礎公式を用いて不静定ラーメンを解く場合には、
　　モーメントのつり合い条件とせん断力のつり合い条件を考慮して、
　　未知量φ及びψを決定し、支店反力及び断面力を決定します。
[たわみ角法の基本式の誘導（２）]

たわみ曲線の微分方程式　d2y/dx2＝−Ｍ/EI　から誘導します。
　　支点Ａと荷重点Ｃの間の曲げモーメントＭxは、
　　Ｍx＝ＭA＋RAx　となります。
　　したがって、たわみ曲線の微分方程式は、
　　ＥＩd2y/dx2＝−Ｍx＝-ＭA−RAx
　　1回積分すると、
　　ＥＩdy/dx＝-ＭA x−RAx2/2＋Ｃ1　となり、x＝０のときdy/dx＝θA　ですから、
　　Ｃ1＝ＥＩθA
　　したがって、ＥＩdy/dx＝-ＭAx−RAx2/2＋ＥＩθA
　　さらに積分すれば、
　　ＥＩy＝-ＭAx2/2−RAx3/6＋ＥＩθAx＋Ｃ2　となり、
　　x＝０のときy＝０　ですから、Ｃ2＝０
　　したがって、ＥＩy＝-ＭAx2/2−RAx3/6＋ＥＩθAx
　　ＡＣ間のたわみ曲線とＣＢ間のたわみ曲線のＣ点において、
　　はりは連続しているため、たわみyとたわみ角dy/dxが等しいことに着目し、
　　x＝aのときyC1とすると、
　　ＥＩyC1＝-ＭAa2/2−RAa3/6＋ＥＩθAa
　　また、x＝aのとき　dy/dx＝θC1とすると、
　　ＥＩθC1＝-ＭAa−RAa2/2＋ＥＩθA

　　次に、ＢＣ間をＢの方よりxをとり、曲げモーメントＭxを求めると、
　　Ｍx＝-ＭB＋RBxとなります。
　　したがって、たわみ曲線の微分方程式は、
　　ＥＩd2y/dx2＝−Ｍx＝ＭB−RBx
　　1回積分すると、
　　ＥＩdy/dx＝ＭBx−RBx2/2＋Ｃ1　となり、
　　x＝０のときdy/dx＝-θB　ですから、
　　Ｃ1＝−ＥＩθB
　　したがって、ＥＩdy/dx＝ＭBx−RBx2/2−ＥＩθB

　　さらに積分すれば、
　　ＥＩy＝ＭBx2/2−RBx3/6−ＥＩθBx＋Ｃ2　となり、
　　x＝０のときy＝０ ですから、
　　Ｃ2＝０
　　したがって、ＥＩy＝ＭBx2/2−RBx3/6−ＥＩθBx
　　x＝bのときyC2　とすると、
　　ＥＩyC2＝ＭBb2/2−RBb3/6−ＥＩθBb
　　また、x＝bのとき　dy/dx＝θC2　とすると、
　　ＥＩθC2＝ＭB b−RBb2/2−ＥＩθB
　　たわみ曲線のＣ点においては、たわみyとたわみ角dy/dxが等しいことから、
　　ＥＩyC1＝ＥＩyC2　より、
　　-ＭAa2/2−RAa3/6＋ＥＩθAa＝ＭBb2/2−RBb3/6−ＥＩθBb
　　ＥＩθC1＝−ＥＩθC2　より、
　　-ＭAa−RAa2/2＋ＥＩθA＝−(ＭBb−RBb2/2−ＥＩθB)

　　ここで、はりＡＢの支点反力RA、RBを求めます。
　　RA＋RB＝Ｐ
　　Ｂ点をモーメントの中心とすると、
　　ΣＭB: RAl−Ｐｂ＋ＭA＋ＭB＝0　より、
　　RA＝1/l(Ｐb−ＭA−ＭB)
　　RB＝1/l(Ｐa＋ＭA＋ＭB)
　　RA、RBを
　　-ＭAa2/2−RAa3/6＋ＥＩθAa＝ＭBb2/2−RBb3/6−ＥＩθBb　に代入し、整理すると、
　　ＭA(a3−3a2l＋b3)＋ＭB(a3−3b2l＋b3)＝3l2(2EI/l)(−θBb−θAa)＋P(a3b−b3a)

　　また、-ＭAa−RAa2/2＋ＥＩθA＝−(ＭBb−RBb2/2−ＥＩθB)　に、RA、RBを代入し、整理すると、
　　ＭA(a2−2al−b2)＋ＭB(a2＋2bl−b2)＝−l2(2EI/l)(−θB＋θA)＋Pabl
　　これら２式より　ＭA 、ＭB　を求めれば、
　　ＭA＝2EK(2θA＋θB)−(pab2)/l2
　　ＭB＝2EK(2θB＋θA)＋(pa2ｂ)/l2 　　ここで、K＝Ｉ/l

　　今、Ｂ点がdだけ下方に移動した場合を考えます。
　　部材回転角R＝d/lとすると、ＭA 、ＭBは、
　　次のようにたわみ角法の一般式が得られます。
CAB 、CBAは、たわみ角の荷重項と呼ばれるもので,θA＝θB＝0　つまり、両端固定の曲げモーメントに等しい。
[節点方程式]

　　ラーメンの節点Ａに集まる部材をＡ1，Ａ2，…,Ａnとします。
　　節点Ａの近傍で各部材を仮想切断すると、
　　その切断面には、図(b)のように材端モーメントＭai(i=1,2,…,n)が生じています。
　　すると、節点Ａ側に残された各部材の断片には図(b)の材端モーメントとつり合いを保つため、
　　逆向きのモーメントが図(c)のように生じています。
　　切断面に生じる材端モーメントは内力であり、
　　節点Ａでつり合い状態にあるため、内力の総和は０になります。

　　また、節点にモーメント荷重が作用している場合は、
　　内力の総和とこのモーメント荷重がつり合うことになります。
　　したがって、節点Ａのモーメントのつり合い条件式は、次のようになります。
　　また、節点Ａに外力としてモーメント荷重Taが時計方向に作用する場合は、
　　各部材端から節点Ａに生じるモーメントの和は、
　　時計方向に外力として作用する荷重とつり合わなければならないから、節点方程式は、
　　節点方程式は、節点の回転角に対して必要なモーメントのつり合い条件式です。
　　例えば、図のようなラーメン構造において、
　　点Ａ，Ｂ，Ｃで節点方程式が得られます。
　　なお、点Ｄ，Ｅでは、回転が拘束されるため、曲げモーメントが生じます。
　　このように回転が拘束されている節点では、
　　節点方程式を立てることはできません。
[層方程式]

　　次にせん断力のつり合い条件式を求めましょう。
　　図に示すようなラーメン構造物を考えます。
　　断面力（内力）は、仮想切断した左右の断面に、
　　同じ大きさで向きが逆に生じています。
　　断面力は部材の変形を引き起こす原因です。
　　部材力の正負を記載する場合、部材の外側が上部になるようにして、
　　はりに置き換えて考えると分かりやすい。
　　仮想切断面の断面力の向きは、正方向に仮定しています。
　　今、ラーメンを水平断面t-tによって
　　上下２つの部分に仮想切断します。
　　断面t-tより上側部分の水平方向の力のつり合いを考えます。
　　切断面t-tは節点Ａの近傍を通っています。
　　節点Ａの切断面には、図のように材端モーメントＭABと
　　せん断力ＳABが生じています。
　　その他の節点の切断面においても同様です。
　　切断面t-tよりも上側で構造物に作用する水平方向の外力（右向きを正）の合力をＳtとすれば、
　　この式を層方程式という。
　　ｎは切断面t-tによって切断された柱の数であり、図ではn=3です。
　　柱Ａ´Ｂ´の両端には、断面力として材端モーメントＭAB、ＭBA及び
　　せん断力ＳAB、ＳBAが生じており、
　　これらの内力と外力P3とで柱ＡＢはつり合っています。
　　柱ＡＢの点Ｂでモーメントのつり合い条件式をたてると、
　　ΣＭB：ＭAB＋ＭBA＋ＳAB・ha＋P3・a＝０
　　∴　ＳAB＝−1/ha (ＭAB＋ＭBA)−(P3・a)/ha
　　P3・aは柱ＡＢに作用する点Ｂのモーメントですから、一般にＭBA0で表すと、
　　荷重が全て鉛直方向に作用する場合や
　　構造物と荷重が左右対称である場合は、
　　右辺は０となるため、層方程式は、

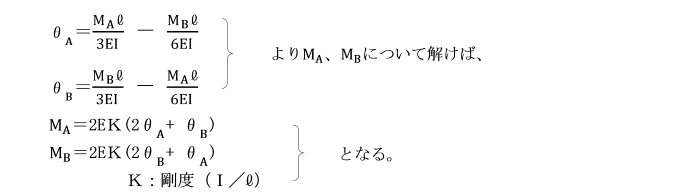
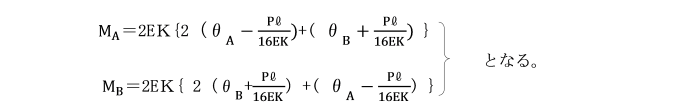
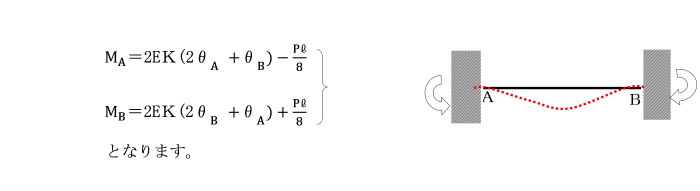
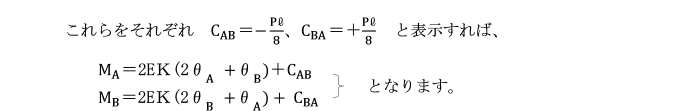
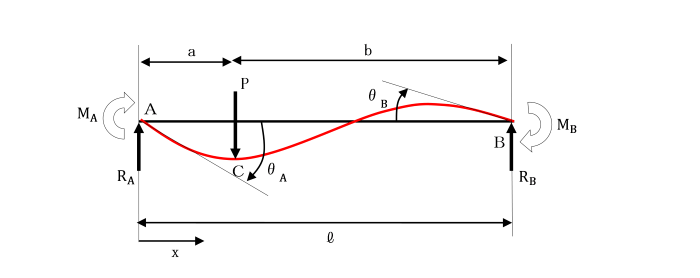
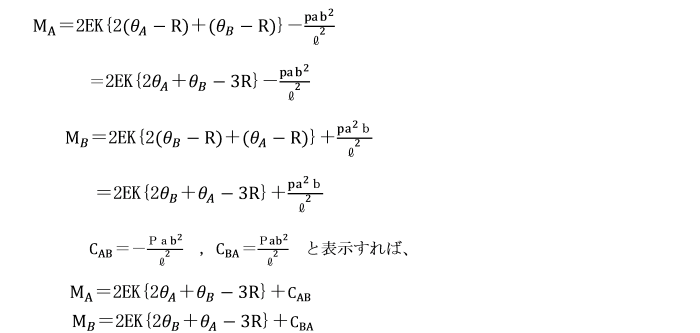
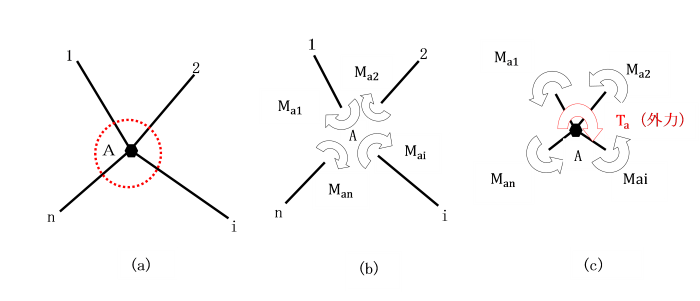
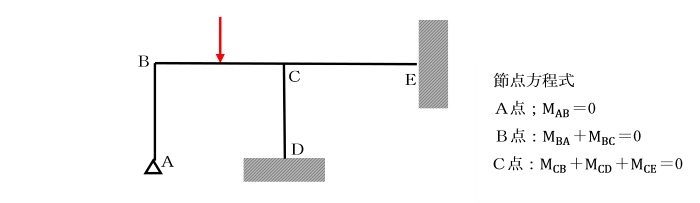
【例題】
　　支点Ａ及びＣで固定されているひじ形ラーメンの水平部材に等分布荷重ｑが作用しています。
　　基準部材に対する各部材の剛比kはいずれも１として、
　　たわみ角法により解きましょう。

【解答】
　　　節点Ｂは移動しないためψ＝０であり、
　　点Ａ及びＣは固定端であるためφA＝φC＝０となります。
　　未知量は節点Ｂの節点回転角φBとなります。
　　部材ＢＡ及びＢＣに対してたわみ角の基礎公式より材端モーメントの式は次のようになります。
　　　　　ＭBA＝kAB(2φB+φA＋ψAB)＝2φB
　　　　　ＭBC＝kBC(2φB+φC＋ψBC)＋CBC＝2φB＋CBC
　　ここにCBCは、たわみ角の荷重項と呼ばれるもので、
　　両端固定のはりＢＣに等分布荷重が載荷されている場合の
　　Ｂ点での曲げモーメントに等しい。
　　CBC＝−ql2/12
　　したがって、節点Ｂの節点方程式は、
　　ＭBA＋ＭBC＝０　となり、
　　材端モーメントの式を代入すると、
　　4φB＋CBC＝０　　∴φB＝ql2/48　となります。
　　この値を材端モーメントの式ＭBA、ＭBCに代入すると、
　　ＭBA＝2φB＝2×ql2/48＝ql2/24
　　ＭBC＝2φB＋CBC＝ql2/24−ql2/12＝−ql2/24
　　さらに点Ａ、Ｃの材端モーメントは、
　　ＭAB＝kAB(2φA+φB＋ψAB)＝φB＝ql2/48
　　ＭCB＝kBC(2φC+φB＋ψBC)＋CCB＝φB＋CCB＝ql2/48＋ql2/12 ＝5ql2/48
　　材端モーメントとはり理論の曲げモーメントの正負の規約が異なるので注意を要します。
　　材端モーメントは、時計回りが正となり、
　　曲げモーメントは、下側引張になるような曲げが正となります。
　　そのため、節点Ａ、Ｂの曲げモーメントをＭA、ＭBとすると、
　　材端モーメントとの間には次の関係があります。
　　ＭA＝ＭAB　　　ＭB＝-ＭBA
　　以上の計算結果より、曲げモーメント図を描きます。
　　柱ＡＢ：
　　ＭA＝１/48ql2　（＝ＭAB）　　　ＭB＝−１/24ql2　（＝−ＭBA）
　　はりＢＣ：
　　ＭB＝−ql2/24　 （＝ＭBC）　　　ＭC＝-5/48ql2 （＝−ＭCB）
せん断力の計算
　　つり合い系T：
　　切断面（節点Ｂの極近傍）t-tの上側
　　t-t断面の上側にある全ての外力（右向きを正）
　　Ｓtは、せん断力ＳBAとつり合う。
　　つり合い系U：
　　柱B´A´
　　ＳBAを求めるために、柱B´A´のつり合い条件式を用います。（切断面における作用・反作用の関係）
　　柱B´A´の両端には、断面力としてＭBA ,ＭAB,ＳBA ,ＳABが生じています。
　　（軸方向力も生じていますが、モーメントのつり合いを考える際には寄与しないので記載していません。）
　　A´点でモーメントのつり合いを考えると、
　　ΣA´：ＭBA＋ＭAB＋hＳBA＝０　となり、
　　ＳBA＝-1/h（ＭBA＋ＭAB）＝−1/h（ql2/24＋ql2/48
　　＝−ql2/16h　となり、右向きに仮定したが左向きに生じます。
　　切断面における作用反作用の関係より、
　　ＳBA＝ql2/16h（右向き）　となります。
　　また、柱B´A´のつり合い条件式ΣＨ＝０より、
　　柱の下端A´の水平せん断力ＳABは、ql2/16hとなり、右向きに生じます。
　　 つり合い系V：
　　切断面（節点Ａの極近傍）s-sの下側
　　ＳABとＳABは作用・反作用の関係からＳABは左向きにql2/16hとなります。
　　したがって、点Ａの水平反力（外力）ＨA＝ql2/16h　は、右向きとなります。
　　同様にＳCBを求めるため、はりB´C´のつり合い条件式を用います（切断面における作用・反作用の関係）。
　　はりB´C´の両端には、断面力としてＭBC,ＭCB,ＳBC,ＳCBが生じています。
　　（軸方向力も生じているがモーメントのつり合いを考える際には寄与しないので記載していません。）
　　Ｂ´点でモーメント（時計回りを正）のつり合いを考えると、
　　ΣB´：ＭBC＋ＭCB＋lＳCB＋1/2ql2＝０　となり、
　　ＳCB＝-1/l（ＭBC＋ＭCB＋ql2/2＝−1/l（-ql2/24＋5ql2/48＋ql2/2）
　　＝−9ql/16　となり、仮定した方向は逆の上向きとなります。
　　また、ＳCBとＳCBは作用・反作用の関係から、
　　ＳCBは下向きに9/16qlとなります。
　　したがって、点Ｃの鉛直反力（外力）ＶCは、上向きに9ql/16となります。

　　次に、ＳBCを求めます。
　　Ｃ´点でモーメント（時計回りを正）のつり合いを考えると、
　　ΣC´：ＭBC＋ＭCB＋lＳBC−ql2/2＝０　となり、
　　ＳBC＝-1/l（ＭBC＋ＭCB-ql2/2）＝−1/l（-ql2/24＋5ql2/48-ql2/2）
　　＝7ql/16　となり、仮定した方向どおり上向きとなります。
　　また、ＳBCとＳBCは作用・反作用の関係から、
　　ＳCBは下向きに7ql/16となります。
　　したがって、点Ａの鉛直反力（外力）ＶAは、上向きに7ql/16となります。
軸方向力の計算
　　部材ＡＢの軸方向力ＮAB＝ＶA＝7ql/16　（圧縮力）
　　部材ＢＣの軸方向力ＮCB＝ＨA＝ＨC＝ql2/16h （圧縮力）

　　以上の計算結果より、ラーメンのＭ図、Ｓ図、Ｎ図を描くと次のようになります。

X　モーメント分配法による解法

　　節点を固定端に置き換えてモーメントと求め、
　　その置き換えた固定端に発生したモーメントを逐次近似する数値解析法で、
　　実用上便利な方法です。
　　連続ばり、不静定ラーメンの節点のモーメントを求めることができます。
[モーメント分配法の適用手順]
　　
　　@　連続ばりの各スパンの支点を固定と仮定し、
　　　与えられた荷重に対する固定端モーメントを求めます。
　　A　各スパンの支点を固定としたことから、
　　　各支点の左右におけるモーメントには違いが生じます。
　　　すなわち「不つり合いモーメント」が生じます。
　　B　実際の連続ばり支点には、不つり合いの状態にはなっていないため、
　　　各支点に生じている不つり合いモーメントをなくすため、
　　　各支点にこの不つり合いモーメントと同じ大きさで逆向きにモーメントを作用させます。
　　C　ある支点に作用させた逆向きの不つり合いモーメントが、
　　　支点の左右にどのように分配されるか（分配モーメント）を調べます。
　　　さらに分配されたモーメントが隣の支点にどのような影響（到達モーメント）を及ぼすか調べます。
　　D　すべての支点で不つり合いモーメントが解消されるまで上記の操作を繰り返す。
　【解説1】
　　図に示すような任意の荷重を受ける３スパン連続ばりの
　　中間支点Ｂ及びＣのたわみ角が０であるためには、
　　支点Ｂ及びＣに作用する外力モーメントTB及びTCの大きさは、
　　TB＝CBA＋CBC
　　TC＝CCB＋CCD
　　となることを示す。
　　ここで、CBA 、CBC、CCB及びCCDは、
　　たわみ角法における荷重項と呼ばれるもので、節点回転角θB、θCは０、
　　つまり、両端固定端の曲げモーメントです。ただし、支点沈下はないものとします。
　　節点Ｂ及びＣの節点方程式は、
　　ＭBA＋ＭBC＝TB
　　ＭCB＋ＭCD＝TC

　　部材ＢＡ及び部材ＢＣに対して材端モーメントの式は、たわみ角の公式より、
　　ＭBA＝k1（2φB＋φA＋ψAB)＋CBA
　　ＭBC＝k2（2φB＋φC＋ψBC)＋CBC であり、
　　支点Ｂ，Ｃは沈下がないため、ψAB＝ψBC＝０となります。
　　ＭBA＋MBC＝TB　に代入し整理すると、
　　2(k1＋k2)φB＋k2φC＝TB−CBA−CBC

　　同様に、部材ＣＢ及び部材ＣＤに対して材端モーメントの式は、
　　ＭCB＝k1（2φC＋φB＋ψBC)＋CCB
　　ＭCD＝k2（2φC＋φD＋ψCD)＋CCD であり、
　　支点Ｃ，Ｄの沈下はないため、ψBC＝ψCD＝０となります。
　　ＭCB＋ＭCD＝TC　に代入し整理すると、
　　k2φB＋2（k2＋k3）φC＝TC−CCB−CCD
　　また、中間支点Ｂ及びＣのたわみ角を０とするためには、
　　φB＝φC＝０　を
　　2（k1＋k2）φB＋k2φC＝TB−CBA−CBC
　　k2φB＋2（k2＋k3）φC＝TC−CCB−CCD
　　に代入すると、
　　TB−CBA−CBC＝0　⇒　TB＝CBA＋CBC
　　TC−CCB−CCD＝0　⇒　TC＝CCB＋CCD　　 となり、たわみ角が０になるようにするには、
　　支点Ｂ及びＣに作用させる外力モーメントTB及びTCを求めることができます。

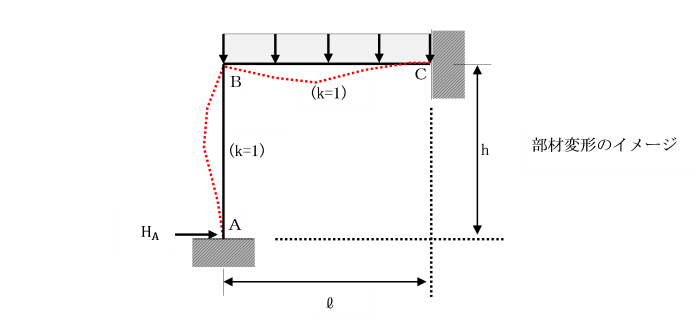
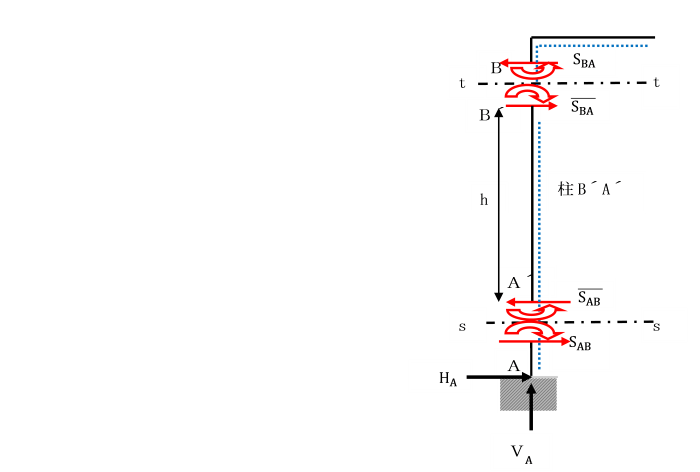
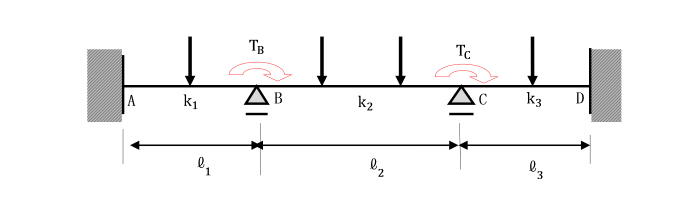
【例題】
　　支点Ａ及びＣで固定されているひじ形ラーメンの水平部材に等分布荷重ｑが作用しています。
　　基準部材に対する各部材の剛比kはいずれも１として、
　　モーメント分配法により解きましょう。

【解答】
　　@　ひじ形ラーメンは、節点Ｂが不動となるため、
　　　図のはりと力学的に同等です。
　　　節点Ｂを固定と仮定し、与えられた荷重に対する固定端モーメントを求めます。
　　　ＢＣに等分布荷重ｑが作用していることから、
　　　点Ｂ，Ｃの固定端モーメント　TB,TCはそれぞれ、
　　　TB＝-ql2/12（反時計回り）　TC＝ql2/12（時計回り）
　　A　支点Ｂを固定としたことから、支点の左右にモーメントの違いが生じます。
　　　すなわち「不つり合いモーメント」が生じます。
　　　支点Ｂに生じている不つり合いモーメントをなくすため、
　　　支点Ｂにこの不つり合いモーメントを逆向きに作用させます。
　　　するとＢＡ、ＢＣには、それぞれの剛比の割合でモーメントが分配されます。
　　　また、支点Ａ、Ｃには到達モーメントとしてそれぞれの1/2が伝達されます。

　　　点Ｂの不つり合いモーメント：−TB＝ql2/12
　　　分配モーメント　ＭBA＝1/(1+1)×(−TB)＝1/2×(ql2/12)＝ql2/24
　　　　　　　　　　　ＭBC＝1/(1+1)×(−TB)＝1/2×(ql2/12)＝ql2/24
　　以上の計算過程から、図（Ａ）,（Ｂ）の曲げモーメント図を重ね合わせたものが曲げモーメント図となります。

Y　定点法による解法

　　定点法は、連続ばりの解法に適用されます。
　　その解法は、三連モーメントの定理における隣り合う支点の曲げモーメントの比、
　　いわゆる定点比というものを導入し、定点比の漸化式を誘導します。
　　その漸化式を用いて、順番に曲げモーメントを求める手法です。
　　詳しい説明は、第８章　構造解析法　8.4 応力法による解法を参照してほしい。
　　（1）定点
　　　　　Ａ端で完全に固定されたはりの
　　　　　Ｂ端にモーメント荷重ＭBを作用させた場合の曲げモーメント図を示す。
　　　　　この場合、曲げモーメントが０になる地点は、
　　　　　Ａ端よりl/3の距離にあり、ＭBの大きさには関係なく決まった点となります。
　　　　　このような点を定点という。
　　　　　定点は、点Ａにモーメント荷重が作用する場合と点Ｂに作用する場合を考えると、
　　　　　一部材に２個存在します。
　　（２）定点比
　　　　　　図に示すように絶対値の大きい方の支点のモーメントを小さい方の支点のモーメントで割り、
　　　　　負号をつけたものを定点比という。
　　　　　定点は、各スパンに左右１個ずつあるから、
　　　　　定点比も各スパンに２個存在します。

　　　　　左定点比：μi＝−Ｍi/Ｍi-1　　 右定点比：νi＝−Ｍi-1/Ｍi
　　（３）定点比の決定
　　　　 [非載荷スパンの場合]
　　　　　連続ばりから隣接する２つの非載荷スパンを取り出し、
　　　　　三連モーメントの定理を適用すると、
　　　　　これらの式は、定点比を決定するための漸化式であり、
　　　　　左定点比μ1が分かれば、以後の定点比を求めることができます。
　　　　　同様にして、右定点比νi+1が分かれば、以後の定点比が順次確定します。

　　　　　[載荷スパンの場合]
　　　　　図のような支点i-1,i間に荷重が載荷されている連続ばりを考えます。
　　　　　TのスパンとUのスパンに3連モーメントの定理を適用します。

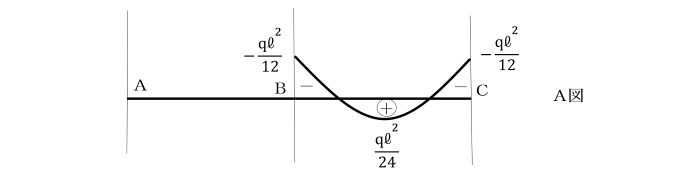
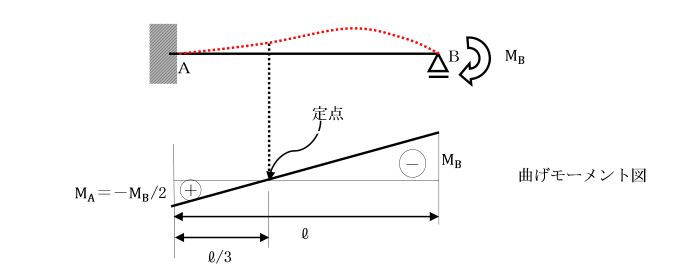
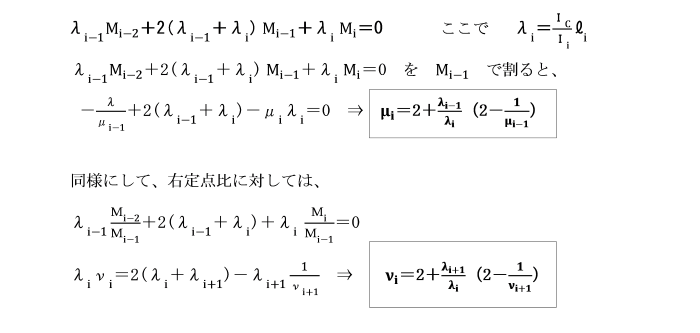
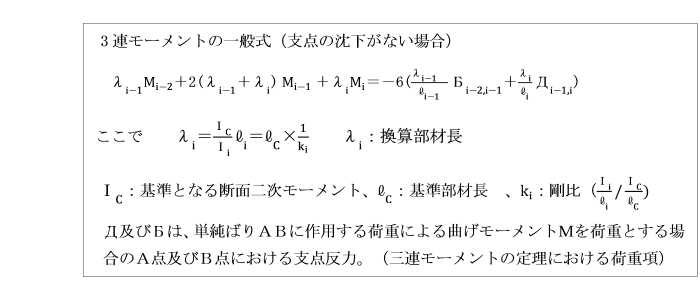
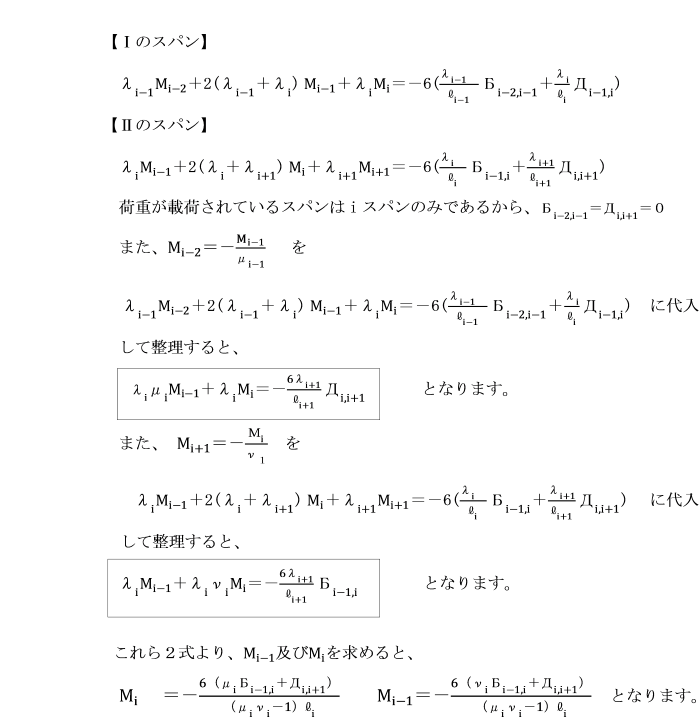
【例題】
　　支点Ａ及びＣで固定されているひじ形ラーメンの水平部材に等分布荷重ｑが作用しています。
　　基準部材に対する各部材の剛比kはいずれも１として、
　　定点法により解きましょう。

【解答】
　　節点Ｂが不動点となるため、図の連続ばりと力学的に同等です。

トップページ