トップページ

第１０章 トラス理論

　３本の直線材の端部を、自由に回転できるピンで相互に連結すると三角形の骨組ができます。
これを三角形構面といい、容易に形を崩すことのない安定した骨組みを形成します。
トラスとは、このような三角形構面が、連続して組み合わせられたもので、
各部材はすべての方向に回転自由なピンで連結されています。
　したがって、部材は軸方向力（引張力もしくは圧縮力）のみに抵抗する構造形式であり、
その他の種類の断面力が生じることがありません。
部材と部材との結合点を節点、あるいは、格点といいます。
構造物内で配列された部材の位置によって、
引張力になるのか圧縮力になるのか、力学的機能が異なるので、
　図に示すように部材に名称がつけられています。
周辺部にある部材を弦材といい、上弦材と下弦材に区別されます。
内側にある部材を腹材といい、
斜め方向に配置されるものを斜材、
鉛直方向に配置されるものを垂直材といいます。

　しかし、実際のトラスの節点は、
部材と部材とを溶接、
または、節点に集まる部材を接合するための板（ガセットプレート）に
ボルトあるいは溶接により添接されています。
摩擦のないピン結合というよりむしろ剛結合に近い。
このため、各部材には、
軸方向力の他に曲げモーメントやせん断力が生じます。
　節点をピン結合であると仮定して計算した軸方向力による応力を
部材応力あるいは１次応力といい、
節点を剛結合することによって生じる曲げモーメントやせん断力を２次応力といいます。
　一般的にトラス部材の断面寸法は、
部材長さに比較して小さく、曲げ剛性も小さい。
そのため曲げモーメント等による２次応力の影響を考慮しなくても、
軸方向力による１次応力のみの計算で設計上支障がありません。
　しかし、港大橋（中央スパン長510m）のような長大トラスの場合には、
部材の断面寸法が大きくなり、
２次応力の影響が大きく、無視できなくなるので注意を要します。

　トラス橋の基本形式は、
ハウトラス・プラットトラス・ワーレントラスの３種類です。
これらの形式は、力学的には、斜材の使い方で区別しています。
ハウトラスとプラットトラスは、
斜材の向きが異なります。
ハウトラスは、斜材が圧縮材になり、
プラットトラスは、引張材として機能します。
斜材は、一般的に部材長が上下の弦材よりも長くなるので、
鋼トラス橋は、引張材になるプラットトラスに採用されます。
ハウトラスは、木造トラスに多く見られます。
ワーレントラスは、斜材の応力がパネルごとに圧縮と引張となります。

10.1　トラス理論における仮定

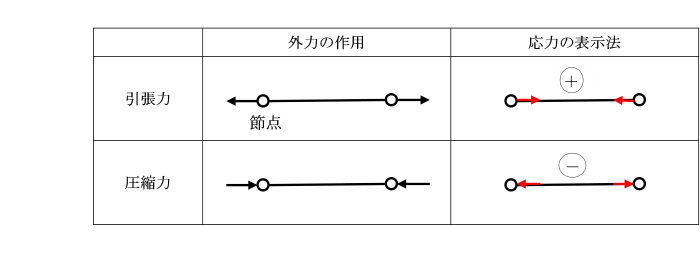
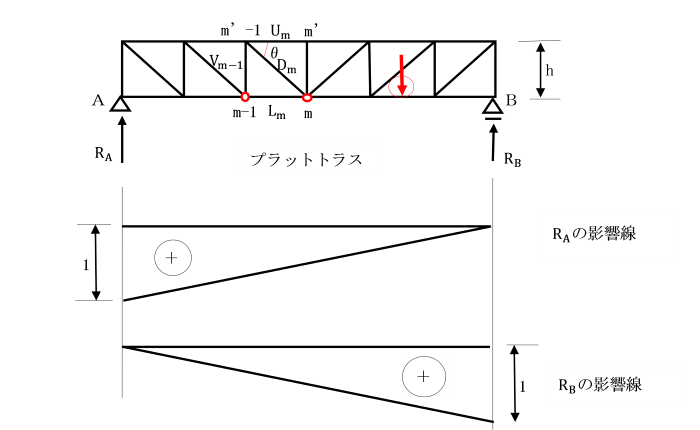
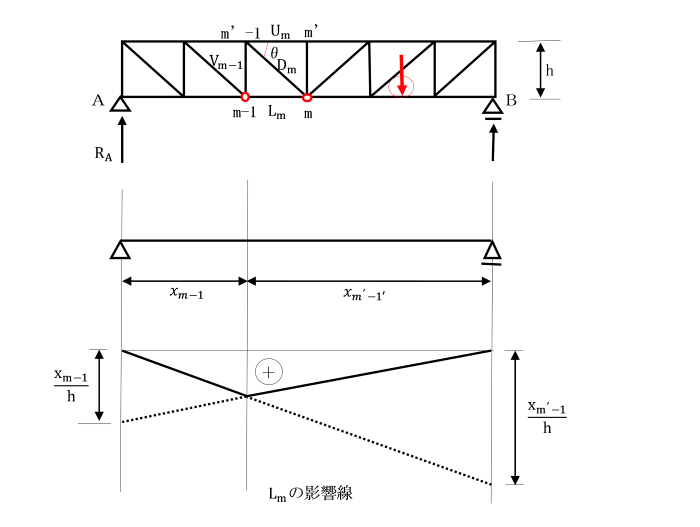
　1．部材は摩擦のないピンで結合されます。（滑節）

　　　曲げ剛性が小さい部材を三角形に構成した骨組構造物においては、
　　節点に作用する外力に対して、軸方向力以外の断面力（曲げモーメント、せん断力）は小さいので、
　　ヒンジ結合として理想化されたトラスと考えても、
　　部材に生ずる応力や節点の変位は、実際の骨組構造物の近似解となります。

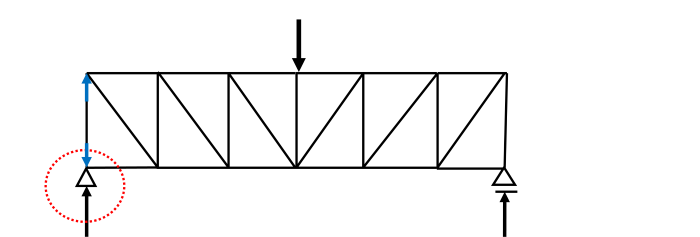
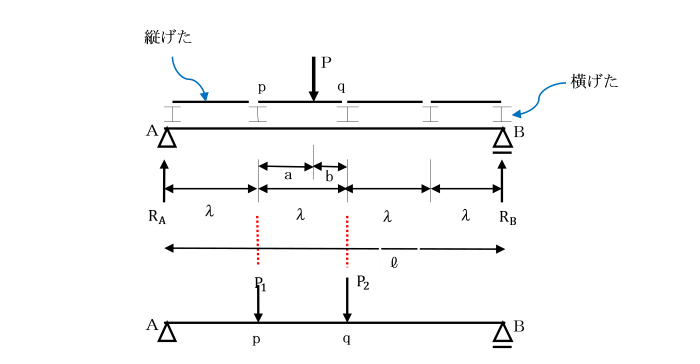
　2．荷重はすべて節点に作用します。（節点荷重）

　　　荷重を節点のみに作用させるためには、
　　荷重が縦桁、横桁をとおして、
　　間接荷重として節点のみに作用するようにします。
　　そのためには、トラスの節点の位置に横桁を設置しなければなりません。
　　　※　節点間に作用する荷重は間接荷重として節点に作用させます。
　　　※　部材には軸方向力のみが生じます。
　　　（曲げモーメントやせん断力は生じない）

　3．各部材は直線材であり、節点の中心を結ぶ直線は部材の軸と一致します。（会合）

　　　１つの節点に接合されている全ての部材の部材軸は、
　　１点を通るとしています。
　　しかし、実際の構造物は、各弦材の断面寸法が異なります。
　　そのため節点付近の継手部は、
　　部材軸が一直線上にならず相互に偏心状態で結合されています。
　　また、腹材をガセットプレートにより弦材に接合するとき、
　　部材寸法や作業空間などのために、
　　２つの腹材の部材軸の交点が、弦材の軸線から偏心することがあります。
　　そのため、節点に回転が起こり、
　　各部材の端に曲げモーメントが生じ、部材に曲げ応力が生ずる一因となります。

　4．全ての外力の作用線は、一平面内にあります。

　5．変形は小さく、いわゆる微小変形理論の仮定が成立します。




10.2　静定トラスの解法

　トラス構造物の部材力は、圧縮力または引張力の軸方向力です。
トラスの解法とは、部材に作用する軸方向力、つまり部材力を求めることです。
部材力を求める方法には、節点法と切断法の２つが存在します。

10.2.1　節点法

　節点法は、節点の近傍で部材断面を仮想切断し、
その節点まわりに作用する集中荷重や
軸方向力をつり合い条件式ΣＨ=０、ΣＶ=０を用いて解く方法です。
つまり、２式から直接的に求められる軸方向力の未知数は２つになります。
１節点に３つ以上の未知数がある場合は、
他の節点からの結果を代入することで順次計算をすすめます。

【節点法の応力計算手順】
@　支点反力を求める。
　　構造全体を剛体ととらえ荷重と反力による外力のつり合いから求めます。
A　解りやすいように各節点に番号（記号）を付けます。
B　各部材の軸方向力を仮定し、記号を付けます。
　　・引張力（＋）に仮定：各節点に対し、節点から離れようとする力と考えます。
　　・圧縮力（−）に仮定：各節点に対し、節点を押そうとする力と考えます。
　　※　軸方向力の符号は引張（＋）、圧縮（−）なので計算を簡単にするために、
　　　　全て引張力が働いていると仮定するのが分かりやすい。
C　各節点ごとにその節点まわりの力（外力）のつり合い式をたてます。
　　・ΣＶ=０　（y軸方向：上向きを＋とします）
　　・ΣＨ=０　（x軸方向：右向きを＋とします）
D　各節点のつり合い式から求められる各部材の軸方向力を順に解きながら、
　　未知数を消去していく。
　（引張応力、圧縮応力の判断）
　　・結果＋：仮定した軸方向力の方向
　　・結果−：仮定と逆の軸方向力の方向

トラスの部材力（引張力、圧縮力）の確認

　トラスに作用する軸方向力が引張力なのか圧縮力なのか、
ハウトラス、プラットトラス及びワ―レントラスを例にとり、
節点法を用いて調べてみましょう。
　その際、トラスに外力が作用しても応力が生じない部材、
いわゆる「０部材」を見つけることも重要です。
その方法を以下に示します。
@　節点にL字型に部材が集まっており、
　　この節点に外力が作用していなければ、２部材とも応力が生じない。
A　節点に部材及び外力が３つ集まっており、
　　その内２つの作用線が同一直線のとき、残りの部材には応力は生じない。
図のハウトラスを例にとり、
部材の力の向き（引張力、圧縮力）を調べてみましょう。
　トラス構造では部材どうしが結合されている各節点において、
力のつり合いが成立しなければなりません。
さらに、トラス部材には軸方向の圧縮力・引張力だけが働くことも併せて考えると、
L字型に集まっている２つのトラス部材の節点に外力が作用しない場合、
２つの部材で力のつり合いを保つことができないので、
両者に軸方向力は働きません。
そのため、左上で囲った部分の部材力は０となります。
　次に、左支点部分について考えます。
支点反力は上向きに作用しています。
上向きの支点反力に対して部材がつり合うためには、
斜材に支点反力と反対向きの方向に部材力が生じなければなりません。
　次に、左支点の下弦材について考えます。
斜材の力の向きが分かったので、これを元に考えます。
斜材に作用する部材力を分解すると、
水平方向の力は左向きなので、下弦材には逆向きの力（右向き）が生じます。
　垂直方向に入っている鉛直材について、軸方向力の向きを調べます。
斜材の部材力を分解すれば、上向きの力が作用しているので、
垂直材には下向きの力が生じます。
　このように、節点法の考え方を用いて、
全ての部材について力の向き（引張力、圧縮力）を調べることができます。
　次に、プラットトラスについて、部材の力の向き（引張力、圧縮力）を調べてみましょう。
　左支点部分について考えます。
上向きの支点反力に対して部材がつり合うためには、
垂直材に支点反力と反対向き（下向き）の方向に、部材力が生じていなければなりません。
　次に、斜材について考えます。
垂直材の力の向きが上向きに力が生じているため、
斜材に生じる力は下向きとなります。
そのため、水平方向に力を分解すると力は右向きとなります。
その結果、上弦材には逆向きの力（左向き）が生じます。
　このように、全ての部材について力の向き（引張力、圧縮力）を調べることができます。
　続いて、ワ―レントラスについて、
部材の力の向き（引張力、圧縮力）を調べてみましょう。
左支点部分において、上向きの支点反力に対して部材がつり合うためには、
斜材に支点反力と反対方向（下向き）に部材力が生じていなければならなりません。
　次に、左支点の下弦材について考えます。
斜材の力の向きが分かったので、斜材に作用する部材力を分解します。
すると、水平方向の力は左向きなので、下弦材には逆向きの力が作用します。
このように、全ての部材について力の向き（引張力、圧縮力）を調べることができます。

10.2.2　切断法（断面法）

　切断法は、任意の部材の軸方向力を求める場合に有効な方法です。
切断法には切断面のつり合い条件式として、
狽g＝０，狽u＝０，狽l＝０ を用いて部材の軸方向力を求める「 カルマン法」と、
任意の位置で３部材を含むように仮想的に断面を切断し、
求めようとする部材以外の２本の部材の交点でモーメントをとる「リッター法」があります。

【カルマン法の部材力計算手順】
　　トラスをある断面で仮想切断し、一方向側の外力と仮想切断面の応力がつり合っているとして、
　つり合い条件式（狽g＝０，狽u＝０，狽l＝０）を用いて求める方法です。
　垂直材と斜材の軸方向力を求めるのに便利です。

　@　支点反力を求めます。
　A　軸方向力を求めようとする部材のある箇所でトラスを仮想切断します。
　　この時、切断する部材数が３材以下となるように設定し、
　　断面力のつり合いを考えます。
　　その際、切断面の部材の軸方向力を引張力となるように仮定します。
　B　切断部材の未知の軸方向力を力のつり合い条件式より求めます。
　　モーメントのつり合い条件式を立てる場合、
　　モーメントの値が０になるような節点を設定することにより計算が容易となります。
【リッター法の部材力計算手順】
　　トラスを任意断面で仮想切断し、一方向側の外力と仮想切断面の応力とのつり合い条件式として、
　狽l＝０のみを用いて解く方法です。
　水平部材の応力を求めるのに便利です。

　@　支点反力を求めます。
　A　軸方向力を求めようとする部材のある箇所でトラスを仮想切断します。
　　この時、切断する部材数が３材以下となるように設定します。
　　その際、軸方向力の符号は引張(＋)、圧縮(−)なので、
　　計算を簡単にするため、全て引張力が働いていると仮定します。
　B　切断部材の未知の軸方向力を３節点について、モーメントのつり合い条件式より求めます。

10.3　トラス解法の選択

どのような形のトラスであっても、ある部材の応力を求める場合、
　@　応力を求めようとする部材を含み、
　　しかも３部材より多い応力不明の部材を含まないように断面を設定します。
　A　その断面でトラスを左右２つに仮想切断します。
　B　応力を求める部材により節点法、切断法を使い分けます。

　　それでは、具体的に図のような上下の弦材が平行であるハウトラスを例に、
　トラスの解法（節点法・切断法）を適用してみましょう。

上弦材Ｕm、斜材Ｄm、下弦材Ｌm及び垂直材Ｖmの応力を求めてみます。
　まずこれら４部材の内、３つの部材Ｕm,Ｄm,Ｌmを切断する断面t-tを考えます。

[上弦材Ｕmの計算]
　Ｕmを除いた他の２つの部材の交点を求めることができる場合は、切断法（リッター法）を用います。
　　@　Ｕmを除いた他の２つの部材（Ｄm、Ｌm）の交点を求めます。
　　　⇒　節点（ｍ−１）をモーメントの中心とします。
　　A　@の節点に対して断面の左側に作用する外力のモーメントを考え、この値をＭm-1とすると、
　　Ｍm-1＝ＲA×2λ−Ｐ1×2λ−Ｐ2×λ
　　B Ｍm-1と上弦材の応力Ｕmがつり合わなければならないため、
　　ΣＭ＝Ｍm-1＋Ｕmh＝0
　　　∴　Ｕm＝−Ｍｍ-１/h となります。

[下弦材Ｌmの計算]
　Ｌmを除いた他の２つの部材の交点を求めることができる場合は、切断法（リッター法）を用います。
　　@　Ｌmを除いた他の２つの部材（Ｕm、Ｄm）の交点を求めます。
　　　⇒　節点ｍ´をモーメントの中心とします。
　　A　@の節点に対して断面の左側に作用する外力のモーメントを考え、この値をＭm´とすると、
　　　Ｍm´＝ＲA×3λ−Ｐ1×3λ−Ｐ2×2λ
　　B Ｍm´と上弦材の応力Ｌmがつり合わなければならないため、
　　　ΣＭ＝Ｍm´-Ｌmh＝0
　　　∴　Ｌm＝Ｍm´/h となります。

[斜材Ｄmの計算]
　Ｕm 、Ｌmが互いに平行であるため、その交点を求められません。
　したがって、「リッター法」は、この部材には適用できません。
　そこで、この部材に対しては、「カルマン法」を適用します。
　断面t-tの左側における外力の鉛直成分の和Ｓmを求めます。
　Ｓm＝ＲA−Ｐ1−Ｐ2
　となり、Ｓmと斜材の鉛直成分がつり合わなければならないから、
　　ΣＶ＝Ｓm＋Ｄm・sinθ＝0
　　∴　Ｄm＝−Ｓm/sinθ 　となります。

[鉛直材Ｖmの計算]
　ある部材の応力を求める場合には、その部材を含む断面で仮想切断する必要があります。
　そこで、Ｖmを仮想切断して、３部材以上仮想切断しない断面t-ｔを考えます。

t-t断面について、つり合い条件式ΣＶ＝0を適用します。
　断面t-tの左側にある外力の鉛直成分をＳm´とすると、
　Ｓm´＝ＲA−Ｐ1−Ｐ2 　　となり、
　これとつり合う部材力はＶmだけですから、
　　ΣＶ＝Ｓm´−Ｖm＝0
　　　∴　Ｖm＝Ｓm´　となります。


節点法を適用します。

[鉛直材Ｖ1]
　ΣＶ＝Ｖ1−Ｐ1＝0
　　∴　Ｖ1＝Ｐ1＝2t（引張）

[鉛直材Ｖ2]
　ΣＶ＝−Ｖ2−Ｐ6＝0
　　∴　Ｖ2＝-Ｐ6＝−8t（圧縮）　…　部材力の向き逆方向

　

切断法（リッター法）を適用します。

[下弦材Ｌ2]

支点反力ＲA
　ＲA＝(2+2+2+2+2+8)/2＝9t
　Ｈ点をモーメントの中心とすると、
　ΣＭH＝ＲA×3−Ｌ2×4＝0
　　∴　Ｌ2＝3ＲA/4＝27/4t

[上弦材Ｕ2]

ＲA＝9t
　Ｅ点をモーメントの中心とすると、
　ΣＭE＝ＲA×9−Ｐ1×6−Ｐ2×3＋Ｕ2×4＝0
　　∴　Ｕ2＝(-81+12+6)/4＝(-9)/4＝−63/4t（圧縮）
　　　※部材力の向き逆方向

10.4　トラスの骨組構成

10.4.1　トラスの安定性

　トラス構造が安定であるということは、次の２点で表されます。
　　@　トラス全体が外力等の作用によって静止（移動しない）していること。
　　　これは、支持条件に関係しており、反力の数により決定されます。
　　　トラス全体が移動しなければ外的に安定しているといいます。
　　　構造物が静止の状態を保つためには、
　　　外力との間につり合い条件式（ΣＨ=０、ΣＶ＝０、ΣＭ＝０）が成立しなければなりません。
　　　このためには、反力の数をｒとすると、ｒ≧３でなければなりません。

　　A　トラスの形状を常に保つこと。
　　　構造物が常にその形状が保たれていれば、内的に安定しているといいます。
　　　トラスでは、部材は軸方向力のみ生じます。
　　　そのため、部材総数をｍ、支点反力の総数をｒとすると、
　　　未知力数の合計はｍ＋ｒとなります。
　　　また、トラスの各節点において外力と内力の間には、
　　　つり合い条件式（ΣＨ＝０、ΣＶ＝０）が成立しなければならなりません。
　　　このつり合い条件式は、節点の数をｊとすると、
　　　トラス全体で２ｊ個成立します。
　　　静定トラスの場合、ｍ＋ｒ個の未知力が、
　　　全て２ｊ個のつり合い条件式によって決定されなければなりません。
　　　したがって、ｍ＋ｒ＝２ｊ　の関係が成立します。
　　　トラスが外的に静定であれば、つり合い条件式（ΣＨ＝０、ΣＶ＝０及びΣＭ＝０）によって
　　　支点反力を求めることができます。
　　　つまりｒ＝３です。
　　　このことから、静定トラスの場合は、
　　　ｍ＋３＝２ｊが成立し、安定したトラスをつくるのに最小限必要な部材数ｍは、
　　　ｍ＝２j−３　の関係式を満足する必要があります。

10.4.2　不静定次数の求め方

赤い実線で示す３本の部材、３個の節点を取り除いた残りの部材について考えます。
　部材数は節点の２倍になっています。
　トラスの部材数をｍ、節点数をｊとすると、
　　　2(j-3)＝ｍ−3　という関係が成立します。

　上式を満足する部材数ｍが、安定したトラスをつくるのに最小限必要な部材数です。
　このトラスは静定トラスといいます。
　これより部材数が少なくなると不安定となり、
　多くなるとより安定となり、不静定トラスとなります。

　不静定トラスには２種類あります。
　支点反力数が４個以上あり、力とモーメントのつり合い条件式だけでは、
　すべての反力を求められない場合です。
　これを外的不静定トラスといいます。

　もう１つは、部材の数が静定トラスの数よりも多く、
　部材力が節点法や断面法だけでは求められない場合、これを内的不静定トラスといいます。

　トラスの不静定次数ｎは、次のように求められます。

　ｎ≧１を満足すれば、不静定トラスですが、
　これだけでは、支点反力が余分にあるのか、部材が余分にあるのか判断できません。
　つまり内的安定か不安定かが判別できません。

　n´を導入することにより判定が可能となります。


【解答】
　(a)　部材数ｍ＝13　,　節点数j＝8　,　反力数r＝4(2+1+1)
　　トラスの不静定次数ｎは、
　　n＝r＋m−２j＝4＋13−2×8＝1
　　　r：支点反力総数　　m：部材総数　　j：節点総数
　 　n´＝ｍ−(2ｊ−3)＝13−(2×8−3)＝0
　　n≧1、n´＝0　であるから、外的、内的安定であり、外的不静定、内的静定です。

　(b)　部材数ｍ＝８　,　節点数j＝6　,　反力数r＝3(2+1)
　　トラスの不静定次数ｎは、
　　n＝r＋m−２j＝3＋8−2×6＝−1
　　　r：支点反力総数　　m：部材総数　　j：節点総数
　　n´＝ｍ−(2ｊ−3)＝8−(2×6−3)＝−1
　　n´＜0　であるから、内的不安定、外的安定か不安定かは、
　　この場合、支点が回転支点と可動支点であるため、外力により移動しない。
　　したがって外的安定であり、外的静定です。

10.5　トラスの影響線

　トラスの解法については、外力が固定している場合を扱っています。
　しかし、トラス橋のように荷重が移動する場合の支点反力、部材力の計算は、
　影響線を利用することが有効です。
　はりの断面力の影響線とトラスの部材力の影響線の違いは、
　はりの場合は特定の断面において考えるのに対し、トラスの場合は、特定の部材について考えるという点が異なります。

10.5.1　トラスの支点反力

　トラスにおいては、任意の位置に荷重が作用しても横げたを介して、
　全て節点に作用するものと仮定しています。

　例えば、図のような間接荷重がはりＡＢに作用しています。

　このような構造において、縦げたに作用している荷重Ｐは横げたを介し、はりＡＢに伝わります。
　つまり、集中荷重Ｐは単純ばりpqの支点反力Ｐ1＝Ｐ・b/λ　、Ｐ2＝Ｐ・a/λに分解されたものです。
　言いかえれば、Ｐ1とＰ2の合力及び作用位置がＰとなります。
　支点反力（ＲA、ＲB）は、Ｐの分力であるＰ1とＰ2の２つの集中荷重を受けるはりとして計算してもかまいませんが、
　支点反力は荷重とのつり合い条件によって決定されるため、
　荷重の位置が分かれば、荷重の伝達方法には無関係に求めることができます。

　先の図を例にとれば、
　ＲA＝（Ｐ1・3λ＋Ｐ2・2λ）/l＝Ｐ(3b+2a)/l＝Ｐ(2λ+b)/l　　となり、
　荷重Ｐが直接はりＡＢに作用している場合と変わりありません。

　したがって、トラスの支点反力は、
　トラスそのものを１つの単純ばりと考えて、単純ばりと同様に求めることができます。

10.5.2　支点反力の影響線

　トラスの支点反力は、トラスそのものが１つのはりと考えられるため、
　支点反力ＲAまたはＲBは、単純ばりの場合と同様に求めることができます。
　したがって、影響線も単純ばりの影響線と同様に求めることができます。

　そこで、図のプラットトラスを例に支点反力ＲA、ＲBの影響線を求めてみましょう。

10.5.3　弦材力の影響線

　[上弦材Ｕmの影響線]
　断面t-tを考え、その左側にあるすべての外力が節点ｍに対するモーメントＭmとすれば、
　ＵmはＭmをトラスの高さhで割り、符号を付ければいい。
　　※　Ｕmを除く他の２部材Ｄm,Ｌmの交点ｍをモーメントの中心とします。
　Ｕm＝−Ｍm/h＝−1/h・Ｍm
　このＭmは、単純ばりＡＢ上を単位荷重Ｐ＝1が移動するときの点mの曲げモーメントです。
　単純ばりの点ｍの曲げモーメントの影響線を求め、−1/h倍したものです。
　曲げモーメントの影響線を描くときには、
　図のように支点ＡＢにおいて、xm/h,−xm'/hの長さをとり、
　単純ばりの場合と同じ方法で作図できます。

[下弦材Ｌmの影響線]

　この場合は、モーメントの中心を節点m’-1にとります。
　　※　L_mを除く他の２部材Ｄm,Ｕmの交点mをモーメントの中心とします。
　Ｌm＝Ｍm'-1/h＝1/h Ｍm'-1
　このＭm'-1は、単純ばりの点m-1の曲げモーメントの影響線を求め、1/h倍したものです。
　したがって、曲げモーメントの影響線を描くときには、
　図のように点Ａ、Ｂにおいて、xm-1/h, xm'-1/hの長さをとり、単純ばりの場合と同じ方法で作図できます。

[斜材Ｄmの影響線]

　この場合Ｄmを除くＵm,Ｌm部材は互いに平行であるため、交点が求められません。
　したがって、リッター法は適用できません。
　カルマン法を用いると、断面t-tがつり合いを保つためには、
　その断面に生じるせん断力Smと斜材Ｄmの鉛直方向はつり合わなければなりません。
　Ｓm−Ｄm・sinθ＝0　より、
　Ｄm＝1/sinθ Ｓm
　すなわち、斜材Ｄmは、その断面のせん断力Ｓmをsinθで割った値です。
　荷重Ｐが節点m-1,m間に作用した場合のこの区間のせん断力Ｓmは、
　はりに間接荷重が作用する場合と同じ影響を受けるため、その間は直線で変化します。
　荷重Ｐが節点m-1,m以外に作用した場合は、荷重が直接作用したときと全く同じになります。
　したがって、単純ばりＡＢのせん断力の影響線を描き、その縦距をsinθで割ればいい。

トップページ